Многие приложения требуют измерения гранулометрического состава. Например, при производстве щебня [1] размеры зерен измеряют с применением специального набора сит, а измерение содержания зерен пластинчатой и игловатой форм (лещадность) проводят вручную [1]. Фракционный состав при производстве щепы [2] измеряют с помощью ситового механического анализатора и весов. В ЦБП от размеров волокон древесной массы зависят её механические свойства, такие как степень помола, разрывная длина, сопротивление раздиранию [4].
Для управления качеством в процессах дробления, рубки, дефибрирования и измельчения необходимы методы оперативного измерения геометрических размеров элементов. Один из возможных способов реализации – применение систем машинного зрения. Здесь надёжное распознавание объектов на изображении и определение их геометрических размеров не представляет сложности в случае, когда все они расположены отдельно друг от друга на контрастном фоне. При расположении группами или слоем границы объектов на изображении не очевидны, что затрудняет их измерение и подсчёт. В таких случаях для определения лещадности щебня и сегментации зерен щебня на изображении некоторые авторы [5] применяют алгоритм водораздела (Watershed). Недостатком такого подхода является то, что размеры сегментов на изображении не равны размерам зерен щебня, так как некоторые зерна перекрывают друг друга в плоскости изображения. В данной работе предлагается метод вычисления информативных признаков, характеризующих фракционный состав хаотично расположенных однотипных упорядоченных структур, присутствующих на изображении, не требующий поиска и выделения объектов. Приводятся результаты применения метода для исследования образцов древесной массы с известными механическими свойствами.
Метод вычисления информативных признаков
Предлагается использовать следующий алгоритм вычисления информативных признаков:
1. Изображение размером N×N пикселов считывается в двумерный массив чисел M[x, y], каждый элемент которого содержит значение яркости пиксела с координатами x, y (темные волокна на белом фоне).
2. Значения элементов массива нормализуются в диапазоне от 0 до 1, причём белому фону (M = MMAX) соответствует значение M′[x, y] = 0.
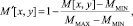 (1)
(1)
где MMIN, MMAX – значения минимальной и максимальной яркости пиксела на изображении.
3. Пусть n1 = 2, а i – обозначает масштаб i = log2(ni) и на первой итерации равно 1.
4. Изображение условно разбивается на смежные квадратные области с размерами ni×ni пикселов, количество которых равно Ni×Ni, причём 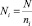 .
.
5. Для каждой смежной области с индексами ix = 0...Ni – 1; iy = 0...Ni – 1 вычисляются суммы:
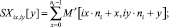 (2)
(2)
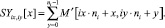 (3)
(3)
6. Затем по известным SXix,iy[y] и SYix,iy[x] для каждой области с индексами ix, iy вычисляются функции FX[m] и FY[m] путем накопления массивов:
FXix,iy[m] = FXix,iy[m] + 1
для всех 1 ≤ m ≤ SXix,iy[y] и y = 0...ni – 1;
FYix,iy[m] = FYix,iy[m] + 1 (4)
для всех 1 ≤ m ≤ SYix,iy[y] и x = 0...ni – 1.
7. Вычисляется суммарное по всем областям значение Di
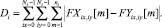 (5)
(5)
8. Если ni < N, то увеличиваем размер области в два раза: ni+1 = 2•ni, увеличиваем i на единицу и повторяем алгоритм, начиная с пункта номер 4.
9. Вычисляется сумма всех элементов массива:
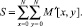 (6)
(6)
10. Процесс повторяется, начиная с первого пункта для всех изображений выборки, при этом суммы Di и S накапливаются.
11. Значения Di нормируются на сумму всех элементов всех изображений выборки:
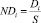 . (7)
. (7)
Ранее данный алгоритм был применен для параметризации изображений волокон древесной массы, сгенерированных при помощи имитационной модели и отличающихся фракционным составом. Было показано [3], что вычисленные таким образом информативные признаки NDi содержат информацию о размерах элементов, представленных на изображениях. Предлагаемый метод был реализован в виде процедуры на C++, которая осуществляет предварительную обработку изображений и выделяет различительные признаки для последующей классификации.
Применим данный алгоритм для параметризации изображений реальной древесной массы различного фракционного состава.
Методика исследования образцов древесной массы
Для исследования взято пять классов (образцов) древесной массы, механические показатели которых были предварительно измерены на стандартном оборудовании специалистами лаборатории оценки качества продукции древесномассного завода АО «Кондопога». Значения этих показателей приведены в табл. 1.
Введем меру различия механических свойств исследуемых образцов древесной массы как евклидово расстояние. Для этого предварительно выполним нормирование каждого из механических свойств по формуле
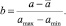 (8)
(8)
Нормированные значения свойств древесной массы представлены в табл. 2.
Таблица 1
Механические свойства исследуемых образцов древесной массы
|
Номер образца (класса) |
а1 |
а2 |
а3 |
|
Степень помола, °ШР |
Разрывная длина, м |
Сопротивление раздиранию, Н |
|
|
1 |
66 |
2350 |
375 |
|
2 |
62 |
2050 |
326 |
|
3 |
77 |
3150 |
352 |
|
4 |
75 |
3050 |
349 |
|
5 |
69 |
2870 |
370 |
Таблица 2
Нормированные значения свойств образцов древесной массы
|
Номер образца (класса) |
b1 |
b2 |
b3 |
b4 |
b5 |
|
1 |
–0,253 |
–0,313 |
0,420 |
0,174 |
–0,151 |
|
2 |
–0,520 |
–0,585 |
–0,580 |
–0,174 |
–0,509 |
|
3 |
0,480 |
0,415 |
–0,049 |
0,413 |
0,380 |
|
4 |
0,347 |
0,324 |
–0,110 |
–0,587 |
–0,211 |
|
5 |
–0,053 |
0,160 |
0,318 |
0,174 |
0,491 |
Таблица 3
Межклассовое различие механических свойств исследуемых образцов древесной массы
|
Номер класса |
1 |
2 |
3 |
4 |
5 |
|
1 |
0,00 |
1,07 |
1,13 |
1,02 |
0,52 |
|
2 |
1,07 |
0,00 |
1,51 |
1,34 |
1,26 |
|
3 |
1,13 |
1,51 |
0,00 |
0,17 |
0,70 |
|
4 |
1,02 |
1,34 |
0,17 |
0,00 |
0,61 |
|
5 |
0,52 |
1,26 |
0,70 |
0,61 |
0,00 |
В табл. 3 приведены значения евклидовых расстояний в пространстве механических свойств для исследуемых образцов древесной массы, полученные по формуле
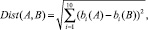 (9)
(9)
где А и В – номера образцов древесной массы в диапазоне от 1 до 5 согласно табл. 1.
Из таблицы видно, что наименее по механическим свойствам отличаются образцы № 3 и 4, а наиболее – образцы № 2 и 3.
Для получения изображений исследуемых образцов древесной массы их концентрации измерены и доведены до (0,0674 ± 0,0006) % абсолютно сухого вещества путем разбавления водой. Измерения выполнялись с помощью высокоточных весов, погрешность которых составляет 0,001 г. Каждый образец тщательно перемешан (дезинтегрирован) с помощью специального миксера и помещен на поверхность четырех предметных стекол. При этом количество раствора контролировалось с помощью весов и составило 0,52 ± 0,03 г. Таким образом подготовлены 20 предметных стекол с образцами древесной массы: по четыре образца каждого из пяти классов.
После сушки всех предметных стекол в горизонтальном положении волокна древесной массы стало удобно наблюдать под микроскопом, так как все они теперь находились в пределах глубины резкости. Далее с помощью специального микроскопа с предметным столиком, позиционируемым шаговыми двигателями, и с помощью специально разработанной для него программы управления предметные стекла были просканированы. В результате этого были получены выборки, содержащие 50–60 изображений с каждого предметного стекла, с разрешением 1024×1024 и размером пиксела изображения – 1,87 мкм.
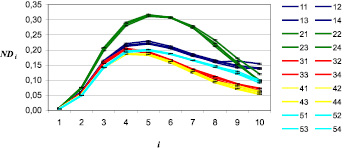
Графики информативных признаков, полученные на основе изображений 20 образцов древесной массы (по 50–60 изображений каждого образца); первая цифра легенды обозначает номер образца (согласно табл. 1)
Результаты исследования образцов древесной массы
Используя выборку из 50–60 изображений, для каждого из 20 образцов были вычислены 10 значений информативных признаков NDi. Результаты представлены на рисунке.
Для оценки информативности предложенного метода вычисления информативных признаков необходимо ввести меру, которая бы характеризовала степень различия образцов в пространстве этих признаков. Так как на графиках не наблюдается резких выбросов, то в качестве меры выбрано евклидово расстояние:
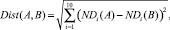 (10)
(10)
где А и В – номера образцов древесной массы в диапазоне от 1 до 20.
Таким образом вычислена матрица евклидовых расстояний размерностью 20×20 между всеми образцами древесной массы. Элементы матрицы, имеющие максимальное значение расстояния между различными образцами, принадлежащими к одному классу, сведены в табл. 4.
Для нахождения межклассового различия вычислены средние значения информативных признаков путем усреднения по четырём образцам, принадлежащим каждому классу, и рассчитана матрица евклидовых расстояний размерностью 5×5 между образцами различных классов, которая приведена в табл. 5.
Из табл. 5 следует, что минимальное евклидово расстояние между различными классами составляет 0,132 (для классов № 3 и 4). Тогда как из табл. 4 следует, что максимальное расстояние между элементами одного класса равно 0,039 (для класса № 2). Следовательно, межклассовое различие более чем в 3 раза превышает максимальное различие между элементами одного класса древесной массы, что говорит о пригодности предложенного метода вычисления информативных признаков для классификации исследуемых образцов древесной массы с различными механическими свойствами.
Таблица 4
Внутриклассовое различие образцов в пространстве информативных признаков
|
Номер класса |
1 |
2 |
3 |
4 |
5 |
|
Мера различия |
0,032 |
0,039 |
0,018 |
0,016 |
0,012 |
Таблица 5
Межклассовое различие образцов в пространстве информативных признаков
|
Номер класса |
1 |
2 |
3 |
4 |
5 |
|
1 |
0,000 |
0,788 |
0,538 |
0,643 |
0,291 |
|
2 |
0,788 |
0,000 |
1,160 |
1,267 |
0,975 |
|
3 |
0,538 |
1,160 |
0,000 |
0,132 |
0,299 |
|
4 |
0,643 |
1,267 |
0,132 |
0,000 |
0,385 |
|
5 |
0,291 |
0,975 |
0,299 |
0,385 |
0,000 |
Коэффициент корреляции механических свойств и полученных информативных признаков образцов древесной массы, вычисленный по данным табл. 3 и 5, равен 0,92. Следовательно, предложенный метод вычисления информативных признаков пригоден для классификации исследуемых образцов древесной массы с различными механическими свойствами.
Работа выполнена при финансовой поддержке программы стратегического развития ПетрГУ на 2012–2016 годы «Университетский комплекс ПетрГУ в научно-образовательном пространстве Европейского Севера: стратегия инновационного развития».



