·Кремний, являясь полупроводниковым материалом, находит широкое применение при изготовлении полупроводниковых приборов: транзисторов, термисторов, фотоэлементов и др. Кремний используется также как добавка к различным сталям и другим сплавам для повышения прочности и коррозионной стойкости. Атомы кремния входят во многие кремнийорганические полимеры, кремнийорганические соединения.
На основе кремния создана телевизионная передающая трубка – термикон, который обладает высокой чувствительностью и сравнительно малой инерционностью.
Несмотря на перечисленные выше качественные показатели применимости кремния, некоторые характеристики еще неизвестны, в частности его межфазная энергия с жидкими металлами σTЖ.
Экспериментальные данные поверхностной энергии расплава кремния σРП можно условно подразделить на две группы, включив в одну группу все величины, имеющие значения меньше 800 мДж/м2, а в другую – данные σРП больше 800 мДж/м2. До тех пор пока не будет экспериментально установлено, какие данные являются действительными значениями поверхностной энергии расплавленного кремния, не будет решена проблема поверхностной энергии твердого кремния σТП. До ответа на этот вопрос лучше вести речь только о порядке величины σТП твердого кремния или об оценке величины σТП.
В настоящей работе сделана попытка оценить межфазные энергии жидких металлов на границе с твердым кремнием, исходя из анализа представленных в работе [10] данных σРП кремния, полученных различными авторами, разными методами и в разное время. Необходимость такого анализа продиктована тем, что некоторые методы, которые в последние годы использовались исследователями для измерения поверхностной энергии расплавленного кремния, например такие, как электростатическая и электромагнитная подвески вызывают недоверие в связи с неотработанностью и отсутствием теоретического обоснования самих методов.
В недавней работе проведен обстоятельный математический анализ экспериментальных данных σРП и ΔσРП/ΔT, полученных различными авторами начиная с 1953 года. Математической обработке подверглись 26 из 27 результатов, представленных в их таблице величин σРП, т.е. за исключением результата одной работы японских авторов в которой получен температурный коэффициент поверхностной энергии ΔσРП/ΔT, расплавленного кремния, равным 0,81 мДж/(м2·К).
Нам представляется, что такой метод отбора результатов для математической обработки является некорректным, так как не учитывает ни надежности применяемого метода измерения, ни условий эксперимента (например, чистота исходного металла (полупроводника), процедура подготовки установки (вакуум или инертная среда)), а также воспроизводимости результатов и т.д.
Из 27 результатов, представленных авторами в таблице, мы отобрали 13 величин σРП и ΔσРП/ΔT кремния. При отборе результатов учитывались следующие факторы: первые 6 величин σРП таблицы, в которых не измерялись ΔσРП/ΔT, не выбраны для определения среднего значения, так как с их помощью можно было бы определить возможность включения или не включения их в список отобранных величин.
Далее, четыре результата работ, в которых ΔσРП/ΔT лежат в пределах от 0,63 до 0,81 мДж/(м2·К), не включены в число отобранных в связи с тем, что расчеты критических температур для них дали результаты меньше температур их кипений, т.е. Тс < Ткип.
В отобранный список не вошли две величины со значениями сильно выходящими из контекста σРП и две величины с очень низкими значениями ΔσРП/ΔT.
Среднее значение σРП по результатам 13 работ оказалось равным 764 мДж/м2, а средний температурный коэффициент поверхностной энергии расплава равен 0,1298 мДж/(м2·К).
В работе [1] были проведены расчеты краевых углов твердых металлов и полупроводников собственными расплавами, в том числе и для кремния. Этот угол θ1 оказался равным 39°.
Ранее нами также была составлена таблица, позволяющая по краевому углу, образуемому расплавом однокомпонентного вещества θ1 и поверхностной энергии расплава σРП, вычислять поверхностную энергию твердого тела при температуре плавления σТП [2]. Из этой таблицы для твердого кремния при температуре плавления найдем
σтп(пл) = 1,1026σРП ≈ 1,1026·764 = 842 мДж/м2.
Затем необходимо определить температурный вклад в поверхностную энергию твердого кремния σтп. Для этого требуется значение температурного коэффициента поверхностной энергии твердого кремния ΔσТП/ΔT. Найдем ΔσТП/ΔT следующим образом. В литературе имеется одно измеренное Гильманом методом раскалывания кристалла значение σТП кремния, равное 1240 мДж/м2 при температуре 78 К [5]. Взяв разность между вычисленным выше значением σТП при температуре плавления и экспериментальным значением, поделив на разность между температурой плавления 1685 К и температурой измерения σТП кремния 78 К, получим ΔσТП/ΔT кремния
ΔσТП/ΔT = (842 – 1240)/(1685 – 78) = –0,2477 мДж/(м2·К).
Зная ΔσТП/ΔT , легко привести поверхностную энергию твердого кремния к температурам измерения краевых углов, образуемых жидкими металлами на поверхности твердого кремния. Для этой цели нужно умножить 0,2477 на разность температур между температурой плавления кремния и температурой измерения θ системы жидкий металл – твердый кремний. В результате получим
ΔσТП = 0,2477·(Тпл – Т),
где Т – температура, при которой измерен краевой угол.
Прибавляя к ΔσТП величину поверхностной энергии твердого кремния при температуре плавления, имеем σтп = ΔσTП + σTП (пл).
При расчете σТЖ разнородных жидкостей и твердых тел, если σРП измерена при другой температуре по сравнению с температурой, при которой измерен краевой угол θ, то σРП также необходимо привести к той температуре, что и θ. Такая процедура перерасчетов σРП нами проведена с жидкими металлами, используя справочные данные из [3].
В качестве примера вычислим σТП и σТЖ при температуре 693 К, при которой измерен краевой угол расплава цинка на поверхности твердого кремния. Сперва найдем температурный вклад в σТП кремния ΔσТП. Для этого умножим ΔσТП/ΔТ на разность температур между 1685 и 693 К. В результате, получим
ΔσТП = 0,2477·(1685 – 693) = 0,2477·992 = 246 мДж/м2.
Прибавляя к этой величине 842, получим
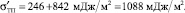
Подставляя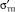 
, σРП цинка 821 мДж/м2, θ = 135° в уравнение Юнга, имеем
σТЖ = ΔσТП – σРПcos θ, (1)
где θ – краевой угол, образуемый расплавом металла на поверхности инородного твердого тела (кремния).
Подставляя в (1) все величины, получим
σТЖ = 1088 – 821 соs135 = 1088 + 821 соs45°= 1088 + 821·0,7071 = 1668 мДж/м2.
Наконец для вычисления работы адгезии жидкого металла воспользуемся формулой
WА = σрп(1 + соsθ). (2)
Для системы расплав цинка – твердый кремний получаем
WА = 821(1 + соs135°) = 821 (1 – 0,7071) = 240 мДж/м2.
Для самопроверки можно использовать также формулу
WА = σрп + σТП – σТЖ. (3)
Результаты по (2) и (3) должны быть, естественно, одинаковыми. По такой же схеме вычислены все межфазные характеристики.
В таблице приведены результаты вычислений поверхностной энергии твердого кремния σТП, межфазной энергии σТЖ и работы адгезии WА некоторых жидких металлов на границе с твердыми кремнием в зависимости от температуры. Краевые углы жидких металлов на поверхности твердого кремния (111) заимствованы из [4].
Анализ вычисленных значений σТП и σТЖ приводит к выводу, что и для контакта однокомпонентного твердого тела с собственным расплавом, и для контакта однородного твердого тела с инородной жидкостью соблюдаются одни и те же закономерности, а именно: при краевом угле меньшем π/2 σТЖ всегда меньше σТП. При θ = π/2, σТЖ = σТП ≠ σРП. При θ > π/2, σТЖ всегда больше σТП. При θ = 180° поверхностная энергия твердого тела и работа адгезии равнялись бы нулю, если бы такие большие краевые углы были возможны в природе. Следует подчеркнуть, что численные значения σТЖ и σТП в случаях однокомпонентных и разнокомпонентных систем будут различными. В связи с тем, что часть σТП, обусловленная температурным вкладом при разнородных твердо-жидких систем рассчитывается независимо от краевого угла, то это приводит к тому, что σТП и при θ = 180° может не равняться нулю. Тогда поверхностную энергию твердого тела можно разделить на две части σТП = ΔσТП + σТП. Часть поверхностной энергии, обусловленная краевым углом, будет равняться нулю, т.е. σТП = 0, а температурный вклад останется, т.е.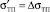 
, следовательно, даже при угле смачивания, равном 180° результирующая поверхностной энергии будет отлична от нуля. С другой стороны, при краевом угле равном нулю, часть межфазной энергии равна нулю, а часть – обусловленная температурным вкладом – также не равна нулю.
Поверхностная энергия твердого кремния и его межфазная энергия с жидкими металлами при различных температурах (мДж/м2)
|
Металл |
T, K |
θ, град |
σрп |
σTП |
σTЖ |
W |
|
Zn |
693 973 1073 |
135 131 130 |
821 748 722 |
1088 1018 994 |
1668 1509 1458 |
240 257 258 |
|
Ga |
323 423 523 |
88 87 87 |
733 724 716 |
1179 1155 1130 |
1153 1117 1093 |
759 762 753 |
|
In |
523 573 673 773 |
111 110 110 110 |
583 578 568 558 |
1130 1117 1093 1068 |
1339 1315 1287 1259 |
374 380 374 367 |
|
Sn |
523 623 723 823 |
130 125 125 125 |
545 535 527 519 |
1130 1105 1080 1056 |
1480 1412 1382 1354 |
195 228 225 221 |
|
Pb |
623 723 823 923 |
130 130 130 130 |
468 460 451 443 |
1105 1080 1056 1031 |
1406 1376 1346 1316 |
167 164 161 158 |
|
Ge |
1263 1313 1343 |
40 30 23 |
634 629 626 |
946 934 927 |
460 389 351 |
1120 1174 1202 |
|
Ag |
1233 |
0 |
926 |
954 |
28 |
1852 |
|
Al |
1023 |
22 |
900 |
1006 |
172 |
1734 |
Выводы
1. Путем подбора научно обоснованных критериев отбора из двадцати семи известных в литературе работ по измерению поверхностной энергии расплавленного кремния нами выбраны тринадцать наиболее достоверных результатов, полученных различными авторами, различными методами, в разное время, и вычислено среднее значение этих величин.
2. Проведена оценка поверхностной энергии твердого кремния при температуре плавления и его температурного коэффициента.
3. С помощью полученного значения температурного коэффициента поверхностная энергия твердого кремния приводилась к температурам, при которых измерены краевые углы жидких металлов к кремнию.
4. По литературным данным углов смачивания твердого кремния жидкими металлами вычислены их межфазные энергии.
5. Показано, что межфазные энергии при θ > π/2 всегда больше, чем σРП смачивающей жидкости и σТП подложки (кремния).