Известно, что преимущество современных подвижных летательных объектов в том, что большие скорости маневрирования затрудняют перехват аппарата в движении. Имеется также возможность использования различных сочетаний высот и скоростей полета: основную часть траектории аппарат летит на большой высоте при малом аэродинамическом сопротивлении, а перед целью выходит на малую высоту, с максимально возможной скоростью полета, что также затрудняет перехват. Существует возможность использования различных маневров на любом участке траектории.
Силовая установка (СУ) сложного летательного аппарата представляет собой короткоресурсный газотурбинный двигатель, а в некоторых случаях – прямоточный воздушно-реактивный двигатель.
К системе автоматического управления (САУ) объектами таких СУ предъявляются, как правило, следующие требования:
- высокая точность поддержания заданных параметров;
- минимальная сложность технического исполнения;
- возможность перехода с одного режима на другой (при совершении маневра) без снижения качества управления.
Для выполнения всех вышеперечисленных требований необходимо разработать новый подход к выбору структуры САУ, к синтезу алгоритмов управления и к их технической реализации. Данное утверждение основано на анализе результатов натурных испытаний и на проведенных ранее теоретических исследованиях.
Поясним на конкретном примере.
Рассмотрим простейшую САУ объектом управления подобного класса (рис. 1, а).
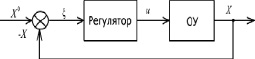
а
б
Рис. 1. а – простейшая САУ ГТД (X0 – заданное значение параметра, X – отработанное значение параметра, ξ – ошибка системы, u – управляющий сигнал); б – предлагаемая структура САУ ГТД с разделенным объектом управления на АДТ и ГТД
Согласно концепции, разработанной ранее [5], исполнительный механизм (ИМ) и двигатель рассматривались как единое целое: неизменяемая часть системы.
Данный подход хорошо зарекомендовал себя при синтезе алгоритмов управления ГТД для гражданских летательных аппаратов или для транспортной авиации. Для таких объектов управления динамические процессы в топливной системе протекают гораздо быстрее, чем в двигателе, поэтому их влиянием на ГТД просто пренебрегали.
Иначе обстоит дело с короткоресурсными ГТД. В них переходные процессы в агрегате топливопитания и двигателе происходят практически одновременно. Данное утверждение неоднократно было подтверждено результатами натурных испытаний [1].
На основании вышесказанного выделим в отдельные звенья непосредственно ГТД и ИМ – агрегат дозирования топлива (АДТ) (рис. 1, б).
При проведении простейшего исследования работы САУ ГТД (рис. 1, б), заключающегося в различных сочетаниях параметров для передаточных функций для ГТД и АДТ, выяснено, что качество управления (точность, наличие перерегулирования, запасы устойчивости) резко изменяется при переходе с режима на режим. Таким образом, задачи анализа качества управления и синтеза алгоритмов управления объектами подобного класса становятся весьма актуальными.
Целью работы является проведение исследования САУ ГТД сложного летательного аппарата с учетом динамики параметров исполнительной части системы и двигателя.
Постановка задачи
Рассмотрим САУ ГТД, показанную на рис. 1, б. Система состоит из элемента сравнения (ЭС), регулятора, АДТ и ГТД. На вход ЭС поступает начальное значение количества оборотов n0 и полученное значение количества оборотов n, на выходе формируется рассогласование поступающих параметров и формируется ошибка системы – ξ. Ошибка поступает на вход регулятора, на выходе формируется управляющий сигнал u, который поступает на вход АДТ, на выходе формируется сигнал расхода топлива Gt, который поступает на вход ГТД и соответственно формируется сигнал n, поступающий на вход ЭС.
Передаточные функции АДТ и ГТД представляют собой инерционные звенья первого порядка, где постоянная времени T = 0,7 с, коэффициент усиления k = 1. Регулятор представляет собой изодромное звено, передаточная функция которого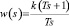 
, при этом коэффициент усиления k = 1, постоянная времени T = 0,7 с.
Необходимо исследовать САУ ГТД и провести анализ качества управления с учетом динамики АДТ и ГТД.
Метод решения
Учитывая то, что в предложенной схеме САУ ГТД объект управления был разделен, целесообразно ввести нелинейные модели отдельно для АДТ и ГТД и моделировать работу системы, учитывая динамику работы ее элементов.
Для того, чтобы исследовать вышеописанную САУ ГТД, предлагается также ввести в структуру системы математические модели АДТ и ГТД, чтобы повысить качество управления всей системы в целом. На рис. 2 представлена схема такой САУ ГТД.
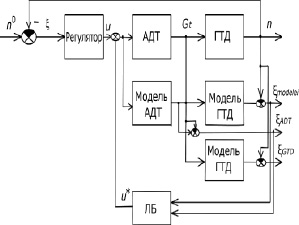
Рис. 2. Предлагаемая САУ ГТД, в которую входит регулятор, АДТ, ГТД, модель АДТ, модель ГТД и ЛБ
В логическом блоке (ЛБ) производится анализ входных сигналов следующим образом: на основе экспериментальных данных и экспертных заключений строится база знаний. Относительно неё формируются функции принадлежностей для входных параметров ЛБ, а также для выходных сигналов. Описание этих подходов достаточно хорошо известно [2]. Сформировав необходимое изменение, ЛБ подает соответствующие сигналы на вход элемента сравнения, формируя сигнал управления, поступающий на вход АДТ и его модели. В ЛБ поступают два сигнала: рассогласование моделей АДТ и ГТД с моделями АДТ и ГТД – ошибка моделей (ξmodelei) и рассогласование АДТ с моделью АДТ – ошибка АДТ (ξADT). Как показывает практика, ошибка ГТД является небольшой и в ходе исследования не учитывается.
Результаты моделирования
Проведем исследование САУ ГТД в графической среде имитационного моделирования Simulink.
Для оценки качества управления САУ ГТД введем следующие требования:
– запас устойчивости по амплитуде: не менее 20 дБ;
– запас устойчивости по фазе: от 35 до 80°;
– перерегулирование: не более 5 %;
– статическая ошибка: не более ±5 % (±0,05);
– время регулирования: не более 5 с.
При моделировании системы (рис. 1, б) было выяснено, что только при значениях постоянной времени (T) для передаточных функций АДТ и ГТД T = 0,7 с, T = 0,5 с, T = 1 с и коэффициенте передачи k = 1 система работает оптимально, соответствуя требованиям качества управления и устойчивости системы. Это говорит о том, что система, изменяет параметры при работе на других режимах, качество управления которой может и не соответствовать требованиям.
Поэтому примем для САУ ГТД значение постоянной времени T = 0,7 с и коэффициента усиления k = 1 и будем считать систему идеальной, взятой за эталон в предстоящем исследовании.
Используя экспериментальные данные, полученные при различных прохождениях трасс, были выбраны точки, связанные с изменением высоты и скорости полета: за время 50, 200, 500 с.
Согласно известным формулам [4], используя экспериментальные данные в выбранных точках, были получены значения постоянной времени и коэффициента усиления для АДТ и ГТД. При моделировании в схеме САУ ГТД модели АДТ и ГТД менялись попеременно с полученными экспериментальными параметрами АДТ и ГТД, что дало возможность проанализировать систему согласно требованиям, описанными выше. В дальнейшем в работе будем использовать время моделирования 50 с, так как его будет достаточно для проведения исследования.
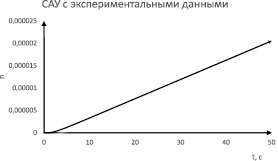
a
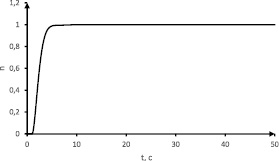
б
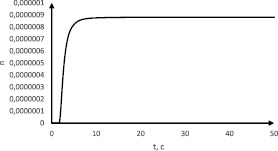
в
Рис. 3. Результаты моделирования САУ ГТД за время моделирования 50 с: a – переходный процесс САУ ГТД с экспериментальными данными (–), САУ ГТД с моделями АДТ и ГТД (- -); б – идеальная САУ ГТД; в – САУ ГТД с моделями
Результаты моделирования САУ ГТД за время 50 с представлены на рис. 3. Моделирование системы проводилось в три этапа: для идеальной схемы, с параметрами, используемыми при проектировании САУ ГТД, а также для системы с экспериментальными данными и системы, использующей вышеописанный подход с математическими моделями АДТ и ГТД для корректировки работы всей системы.
Как видно из рисунка, переходный процесс с идеальными параметрами передаточной функции для АДТ и ГТД устанавливается за время регулирования, которое составляет 5 с; система же с экспериментальными значениями достаточно инерционна и не соответствует требованиям качества управления и устойчивости, для корректировки САУ ГТД были введены математические модели АДТ и ГТД, которые уменьшили время регулирования и стали соответствовать требованиям.
Как видно из рис. 3, в, переходный процесс предложенной САУ ГТД уступает в качестве: значение не достигает единицы. Тем самым, для увеличения точности переходного процесса, предлагается ввести ЛБ на основе нечеткой логики, база знаний и функции принадлежностей которого для входных и выходных параметров будут соответствовать графику зависимости ошибок от управляющего сигнала (рис. 4).
Для обеспечения приемлемого характера переходного процесса предлагаемой САУ ГТД предлагается ввести еще один регулятор: интегрирующее звено. Экспериментальное моделирование показало, что для интегратора значение коэффициента усиления (k) равное 150 стало достаточным, чтобы увеличить качество выходных параметров. На рис. 5 представлен такой переходный процесс, а также на график нанесено несколько точек, характеризующих идеальный процесс.
Такое параметрическое и структурное изменение дало возможность качественно изменить выходные параметры системы с экспериментальными данными и приблизиться к выбранным в статье идеальным параметрам. Идея введения математических моделей АДТ и ГТД в контур управления отражена в патенте [3].
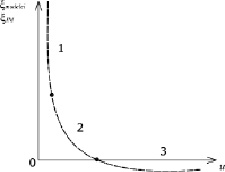
Рис. 4. Зависимость ошибок моделей и АДТ (ξmodelei, ξADT) от управляющего сигнала u с разделением на зоны: 1 – минимальная, 2 – средняя, 3 – максимальная
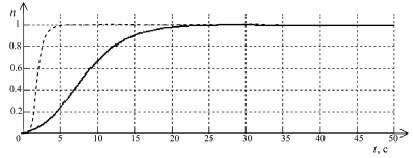
Рис. 5. Переходные процессы САУ ГТД с моделями и введением интегратора в структуру (—), идеальной ГТД (- -)
Выводы
Результаты моделирования исследуемой САУ ГТД показывают правомерность предложенного подхода с целью повышения качества управления. Разделение объекта управления на АДТ и ГТД позволяет учитывать динамику исполнительной части системы и двигателя, появляется возможность использовать рассогласование между частями структурной схемы САУ ГТД, тем самым увеличивать надежность и устойчивость работы системы на различных режимах. Интеллектуальный подход позволил сформировать ЛБ, который качественно улучшил выходные параметры системы и позволил приблизиться к идеальным с достаточной степенью точности.