В современных условиях хозяйствования весьма актуальной является проблема обеспечения экономики России высококвалифицированными кадрами. Номенклатура направлений и специальностей, существующая в стране, структура приема и выпуска специалистов во многих случаях не соответствует потребностям народного хозяйства не только в перспективе, но и в реальном времени. Это видно как на отраслевом, так и на региональном уровнях, где наблюдается существенная дифференциация в трудоустройстве выпускников.
На рис. 1 приведена динамика распределения занятых в экономике России по занятиям. Видно, что в 2014 г. по сравнению с 2000 г. в два раза выросла доля руководящих работников, что является скорее негативным, нежели позитивным результатом. Вместе с тем, виден существенный рост доли специалистов высшего уровня квалификации, сопровождающийся не менее существенным уменьшением доли неквалифицированных рабочих. Таким образом, рынок диктует необходимость существенного повышения уровня образования, что сопровождается увеличением доли специалистов с высшим образованием практически во всех отраслях экономики [4, с. 114].
На рис. 2 приведена динамика распределения занятых в экономике России по видам экономической деятельности [4, с. 116]. Здесь мы видим значительное сокращение с 2000 по 2014 гг. доли занятых в сельском хозяйстве и в промышленности. Причина может быть связана с ростом производительности труда (с 2005 по 2014 гг. она выросла в обрабатывающих производствах на 33,6 %, тогда как в строительстве – только на 5,1 %). При этом существенно возросла доля занятых в торговле.
Анализ рис. 3 позволяет сделать выводы о наличии существенной текучести кадров практически во всех видах производственной деятельности [4, с. 128]. Выбытие работников почти всегда превышает прибытие и составляет от 15 до 45 % от списочного состава работающих. Выбытие связано со следующими причинами:
– естественная убыль (уход на пенсию, смерть);
– добровольный уход работников в связи с желанием найти более интересную (высокооплачиваемую) работу;
– увольнение по инициативе работодателя (конфликт, низкая квалификация и т.д.).
В свою очередь, принятие на работу может осуществляться либо в результате перехода с другого предприятия, курсов переподготовки, либо по окончании учебного заведения.
Для анализа потребности региона в кадрах можно использовать следующую модель. Пусть li – количество занятых в i-й отрасли экономики; vi – доля занятых с высшим образованием; ai – доля принятых в течение года выпускников образовательных учреждений в общем числе занятых; bi – доля принятых в течение года работников других предприятий (отраслей, регионов); ci – доля выбывших в течение года работников i-й отрасли экономики в результате естественных причин; di – доля выбывших в результате добровольного ухода или увольнения (миграция); Ti – среднее число периодов (лет) трудовой деятельности работника i-й отрасли; si – коэффициент роста (снижения) потребности в кадрах для i-й отрасли из-за изменения производительности труда, структурной перестройки экономики и т.д.
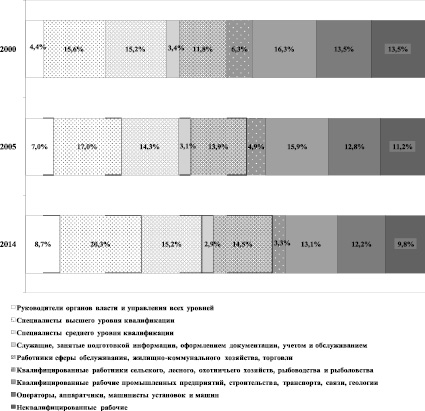
Рис. 1. Динамика распределения занятых в экономике России по занятиям, %
Рис. 2. Динамика распределения занятых в экономике России по видам экономической деятельности
Если предположить равными миграционные коэффициенты прибытия и убытия (bi = di), то при неизменной численности работающих ai = ci = Ti-1. В этом случае требуемое число выпускников организаций ВПО для i-й отрасли экономики в данном регионе с учетом изменения потребности в кадрах
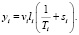(1)
Эта потребность должна обеспечиваться имеющимся в регионе ресурсами:
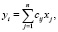(2)
где xj – число выпускников j-й специальности (группы специальностей), наиболее соответствующей j-й отрасли народного хозяйства региона;cij – доля выпускников j-й специальности, востребованная для i-й отрасли экономики,
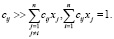
Имеем систему линейных уравнений, которая аналогична системе, описывающей межотраслевой баланс экономики (модель Леонтьева) [2]:
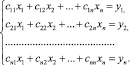(3)
Данная система легко решается численно с использованием итерационных методов [5]. Итерационная формула для нахождения вектора неизвестных имеет вид
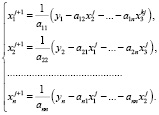(4)
Задача существенно упрощается в том случае, когда матрица C является диагональной (содержит единицы на главной диагонали, остальные – нули). Это может иметь место для таких отраслей, как медицина, образование, сельское хозяйство и др., где почти не требуются специалисты других направлений подготовки. В этом случае xi = yi, то есть требуемое число выпускников i-й группы специальностей должно равняться спросу со стороны предприятий соответствующей отрасли народного хозяйства региона.
Вместе с тем предложение выпускников может существенно отличаться от спроса. Для анализа соответствия уровня выпуска потребности региона в специалистах введем следующие коэффициенты:
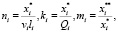(5)
где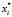 
– фактический уровень выпуска специальности (группы специальностей), соответствующей i-й отрасли народного хозяйства региона, 
– число выпускников, трудоустроившихся по специальности, Qi = pili – объем выпуска продукции отрасли, pi – производительность труда.
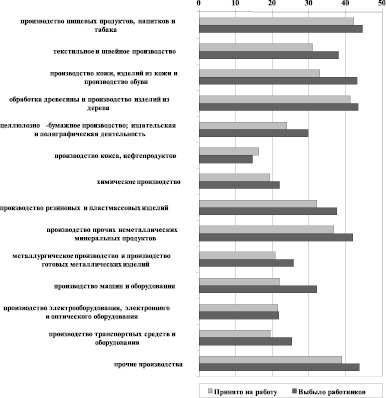
Рис. 3. Прием и выбытие работников по виду экономической деятельности «Обрабатывающие производства» в России в 2014 г., в % от списочной численности
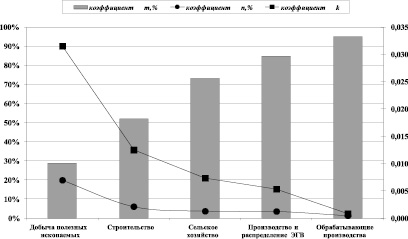
Рис. 4. Коэффициенты соответствия спроса и предложения на рынке образовательных услуг для различных отраслей экономики Нижегородской области (данные 2014 г.)
Коэффициент mi свидетельствует о превышении предложения над спросом в случае низкого уровня трудоустройства, а коэффициенты ni и ki в простейшем случае служат индикаторами баланса спроса и предложения кадров в i-й отрасли экономики:
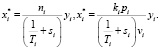(6)
Таким образом, если
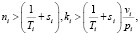(7)
то наблюдается превышение предложения над спросом, в противном случае – превышение спроса над предложением.
На рис. 4 приведены результаты расчетов коэффициентов mi, ni, ki для различных отраслей экономики Нижегородской области (данные 2014 г.). Использовалась информация Росстата [3], а также данные мониторинга вузов, проводимого Минобрнауки РФ [1].
Из рисунка видно, что в группе «Обрабатывающие производства коэффициент ni лишь немногим превышает 1 %, а в группе «Производство и распределение электроэнергии, газа и воды (ЭГВ)» он составляет около 3,5 %. Это свидетельствует о том, что в этих промышленных группах спрос на выпускников равен или немного превышает предложение. Об этом же свидетельствуют невысокие значения коэффициента ki, а также близость к 100 % индикатора трудоустройства. В то же время в группе «Добыча полезных ископаемых» наблюдается обратная картина, когда коэффициент ni равен 90 %, а уровень трудоустройства – 20 %. Это говорит о том, что предложение выпускников данной группы в регионе существенно превышает спрос.
Приведенные диаграммы подтверждают диагностические возможности предложенных выше коэффициентов. Это использовалось авторами в предыдущих работах при апробации изложенных методических подходов к анализу и прогнозированию потребности в инженерных кадрах для различных регионов страны. Так, в книге [7] приведен анализ агрегированного коэффициента k, рассчитанного как отношение приведенного контингента учащихся на технических специальностях промышленной направленности к объему промышленного производства в регионах России, по всем инженерным направлениям. Анализ результатов показал, что в Московской, Ленинградской, Новгородской, Кировской и Тюменской областях, Республике Алтай, Чукотском АО и Камчатском крае наблюдается дефицит выпускников инженерных специальностей. В свою очередь, в Ивановской области, Республиках Бурятия и Тыва – их избыток. Нулевое значение показателя у Республики Калмыкия связано с отсутствием приведенного контингента учащихся на технических специальностях промышленной направленности. В Республиках Дагестан, Чечня и Северная Осетия-Алания, наоборот, наблюдаются аномально высокие значения, что связано с практическим отсутствием промышленного производства.
В работе [6] приведен сравнительный анализ регионов по результатам расчета коэффициента ki для металлургической отрасли. Нехватка кадров для металлургического производства наблюдается в Ленинградской, Вологодской, Сахалинской и Магаданской областях, Республиках Калмыкия, Алтай, Тыва, Чукотском автономном округе, Еврейской автономной области. В то же время превышение значения индикатора требуемого значения для ряда регионов может свидетельствовать как об избытке выпускников группы специальностей «Металлургия, машиностроение и материалообработка», так и об их востребованности на других производствах.