Одним из способов повышения эффективности проведения научных исследований является использование сети центров коллективного пользования (СЦКП), которые обладают значительным научным потенциалом и включают уникальное научно-исследовательское оборудование [2, 4]. Это объясняется тем фактом, что проведение современных научных исследований сопряжено со значительными техническими и финансовыми затратами, что делает необходимым оптимизацию расходов и использование инновационных технико-экономических подходов.
Научно-образовательная инфраструктура Национального исследовательского университета «МИЭТ», который осуществляет подготовку специалистов в области базовых этапов технологического процесса изготовления изделий электроники, включает центры коллективного пользования (ЦКП) «Диагностика и модификация микроструктур и нанообъектов», «Микросистемная техника и электронная компонентная база», «Поверка и калибровка электронных приборов и оборудования», которая при необходимости может быть расширена за счет ЦКП предприятий и организаций-партнеров.
Сеть центров коллективного пользования МИЭТ является базой для создания специализированного кластера микроэлектроники с индивидуальной отраслевой специализацией и соответствующей группой предприятий-партнеров [1, 5].
Стандартная методика проведения научных исследований с использованием высокотехнологичного научного оборудования базируется на объединении всех имеющихся ресурсов сети центров коллективного пользования, которые в совокупности представляют собой потоки материальных ресурсов, теоретической основой которых является теория массового обслуживания [2, 3].
При этом достаточно актуальной является проблема обеспечения эффективного управления потоками материальных ресурсов сети ЦКП, разработка механизмов, обеспечивающих оперативное формирование и пополнение запасов материальных ресурсов для определенных научных исследований [4].
Одним из эффективных решений данной проблемы является создание теории мультикритериального управления потоками материальных ресурсов, которая обеспечивает обоснованный выбор оптимального в данных условиях времени алгоритма управления. Создание подобной теории направлено на значительное улучшение эффективности работы системы управления материальными ресурсами сети ЦКП, связанное с повышением эффективности пополнения и распределения материальных ресурсов, запасов и материалов.
Авторами была предложена теория мультикритериального управления материальными потоками, которая обеспечивает рациональное пополнение запасов ресурсов другими словами на основе характеристик входного потока заявок, а также текущего состояния системы управления; формируется выходной поток заявок, который через внешнюю систему генерирует ответный входной материальный поток, обслуживающий поступающие заявки с минимальными затратами [8, 10].
В основе разработанной теории мультикритериального управления материальными потоками лежит использование совокупности иерархически упорядоченных матриц [7, 9], например:
- Матрица инициализации М1, которая обеспечивает отбор алгоритма для ресурса, который на предыдущем этапе не обрабатывал никакой логистический алгоритм. Применение матрицы инициализации обеспечивает на этапе первичного создания резервов материальных ресурсов применение нестандартных стратегий управления (например, осуществление заказов и создание резервов таких ресурсов с различной степенью интенсивности: либо для первоначального накопления, либо для уменьшения последствий неправильного принятого решения о резервировании);
- Итоговая матрица М2, которая определяет условия, при выполнении которых материальные ресурсы лишаются назначенных им ранее алгоритмов управления. По аналогии с матрицей инициализации здесь возможны несколько подходов в зависимости от требуемой оперативности расформирования ресурсов.
- Рабочая матрица W3 определяет условия, при которых можно сменить алгоритм управления для определенного типа ресурса.
В соответствии с предложенной теорией механизм управления материальными ресурсами сводится к разделению всех ресурсов R на два типа: ресурсы, которые обрабатываются определенным AR, и все остальные. Ресурсы второго типа фильтруются матрицей инициализации, которая решает вопрос о необходимости их резервирования [6, 8]. Ресурсы первого типа обрабатываются с помощью итоговой матрицы и если ресурс не исключается, то он отправляется в рабочую матрицу, которая в случае необходимости осуществляет смену алгоритма управления:
,
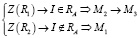где Z(R1) и Z(R2) – процедуры обработки первого и второго типа ресурсов соответственно.
Представленные выше матрицы, количество которых в общем случае может быть больше трех, могут также обладать и внутренней иерархией, в частности, когда одна из ячеек итоговой матрицы содержит указание не отменять назначение соответствующего алгоритма, а наоборот дополнительно фильтровать ресурс через еще дополнительную итоговую матрицу, с более низким уровнем иерархии, что позволяет обеспечить процесс мультикритериального отбора.
Зачастую в реальных ситуациях заявки на ресурсы поступают циклично с переменной интенсивностью. В этом случае прогнозирование потребления ресурсов целесообразно осуществлять не на основе среднего потребления за всё время сбора статистики, а на основе среднего потребление за время цикла. И далее осуществлять прогнозирование потребления в следующем цикле.
Учитывать цикличность запросов на материальные ресурсы сети ЦКП можно двумя способами:
– используя обычную матрицу отбора, не учитывающую факторы цикличности и сезонности с использованием алгоритмов, которые при прогнозировании потребления ресурсов распознают в исторических данных циклическую составляющую. Недостаток данного способа состоит в том, что подобным алгоритмам для повышения эффективности работы (снижения ошибки: расхождения практики, реальности и прогноза) обычно требуют сложных вычислений и большой ресурсной ёмкости (зачастую требуется проанализировать большой объем данных) . При этом на практике обычно такая сложность заведомо является избыточной – например, эксперт может заранее знать, что данные обладают цикличностью. В таком случае применение алгоритма, пытающегося самостоятельно найти цикличность и её параметры, представляется нерациональным.
– использование в матрице отбора процедуры пополнения агрегирующих критериев, а именно: периодов запросов и серий периодов запросов. И дальнейшее построение осей матрицы на их основе [6, 7, 10]. При этом подходе возможно использовать обычные, простые алгоритмы прогнозирования.
Далее рассмотрим критерии, которые работают не непосредственно с исходными данными, которые получены в процессе эксплуатации системы, а со сформированными на их основе агрегатами. В частности, такой показатель, как количество запросов, является агрегатом показателя «потребность», но в аспекте обращения за ресурсами показатели – разделение потребности по обращениям и подсчёт числа разделений становятся фактически агрегирующими критериями.
Такими агрегирующими критериями могут, в частности, являться:
а) период запросов, то есть количество периодов для некоторого временного интервала, для которого запросы из этих периодов удовлетворяют заданным критериям (пример: число недельных периодов в году, при условии, что для каждого периода существовало не менее одного запроса ресурса), как представлено на рис. 1;
б) линейка периодов запросов, то есть количество идущих подряд без прерываний периодов запросов, как представлено на рис. 2.
По аналогии могут быть использованы и другие агрегирующие критерии, которые основаны на прочих исходных данных (стоимости ресурса, валовой величины ресурса, и т.д.). Эффективность их применения оценивается для каждого конкретного случая в зависимости от используемых алгоритмов, целей и задач управления ресурсами сети ЦКП. Вместе с тем предложенная методология агрегирования обеспечивает весомые преимущества при построении систем управления их алгоритмов.
Зачастую в практических задачах потребности в различных ресурсах бывают логически взаимосвязаны. В частности, потребность в ресурсе «диагностический комплекс» почти всегда приводит к наличию потребности на ресурс «программное обеспечение». В этом случае имеет смысл в планировании ресурса использовать спецификации, дающие описание подобных связанных ресурсов.
Некий ресурс вида A назовем ведущим, а ресурсы видов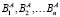 
– ведомыми, в случае, если имеющаяся потребность в ресурсе A приводит к возникновению потребности на ресурсы 
.
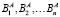Далее введем понятие спецификации, которую определим в виде дерева связи ресурсов. Она может быть одно- или многоуровневой, как представлено на рис. 3.
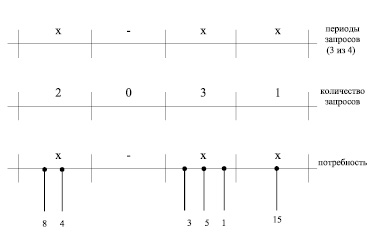
Рис. 1. Агрегирующий критерий «периоды запросов»
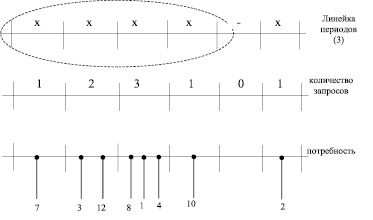
Рис. 2. Агрегирующий критерий «линейка периодов запросов»
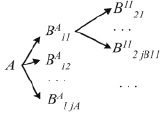
Рис. 3. Древовидная спецификация видов ресурсов
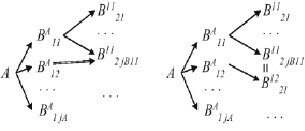
Рис. 4. Преобразование сетевой спецификации видов ресурсов в древовидную
Все виды ресурса, которые относятся к одной спецификации, назовём связанными. Основной ресурс, с которого идет построение спецификации (дерева), назовем корневым – в данном случае это ресурс вида «A». Для дерева, аналогично обычным деревьям, можно определить глубину (высоту) как число уровней в спецификации и ширину (толщину) как максимум, по всем уровням из числа элементов некоторого уровня.
Обход спецификации осуществляется обычными алгоритмами для деревьев – «поиск в ширину» и «поиск в глубину». Ветви дерева возможно взвесить количеством ведомого ресурса, приходящегося на одну единицу ведущего ресурса. Также представляется рациональным не преобразовывать дерево в сеть, если один из видов ресурса используется на разных уровнях, а рассматривать такие виды ресурса как различные и после окончания планирования сводить потребность в них воедино суммированием (рис. 4). Планирование связанных ресурсов с помощью теории мультикритериального управления возможно тремя основными способами: наличие спецификации никак не учитывается, все ресурсы планируются независимо; все ведомые ресурсы не планируются: потребность в них получается путем планирования потребности в корневом ресурсе и дальнейшего прохода (в ширину или глубину) по дереву видов ресурса; потребность в ведомых ресурсах вычисляется аналогично второму варианту, но потом она дополняется по первому варианту.
Пример: потребность в ресурсе «диагностический комплекс» приводит к наличию потребности на ресурс «программное обеспечение», однако из-за сбоев в работе комплекса, приводящих к повреждению некоторых подпрограмм, потребность в ПО превышает расчётную по спецификации. Это превышение и планируется статистически (без учета спецификации).
Выводы
Предложенная методика учета цикличности запросов при мультикритериальном управлении потоками материальных ресурсов [6–8] обеспечивает: поиск цикличности в поступлении запросов на ресурс и учёта её в селективной матрице и выбранном ей алгоритме; более эффективное отсеивание спорадических всплесков-запросов ресурса, особенно в случае, когда запрос потребителя, по тем или иным причинам, поступил в систему не единым запросом, а был разбит на несколько запросов в течение периода.