Система уравнений Лотки – Вольтерры находит применение не только в природе, но также часто используется при моделировании экономических систем. При этом часто экономические системы сравниваются с биологическими, где в качестве энергии выступает биомасса, а в экономических системах – капитал. Эти уравнения применимы при моделировании различных типов взаимодействия между видами, таких как системы «хищник ? жертва», «паразит ? хозяин», конкуренции так далее.
Опишем на математическом языке данное взаимодействие. В математической форме оно имеет следующий вид:
(1)
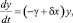
где x – количество жертв; y – количество хищников; t – время; α, β, γ, δ – коэффициенты, отражающие взаимодействия между видами.
Допустим, у нас есть закрытый ареал, существа которого не иммигрируют и не эмигрируют. Также допустим, что еды для травоядных животных у нас имеется с избытком.
Диаграмма причинно-следственной связи данной системы представлена на рис. 1.
Тогда уравнение изменения количества жертв примет вид:
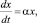(2)
где α – это коэффициент рождаемости жертв; x – это величина популяции жертв;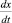 
– это скорость прироста популяции жертв.
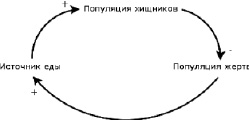
Рис. 1. Пищевой обмен в системе «хищник-жертва»
Так как хищники стабильным питанием не обеспечены, то они вымирают. Следовательно, уравнение для хищников примет вид
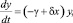(3)
где γ – это коэффициент убыли хищников; y – это величина популяции хищников;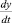 
– это скорость прироста популяции хищников.
Таким образом, при встречах хищников и жертв (частота которых прямо пропорциональна величине xy) происходит поглощение жертв с коэффициентом β и рождение новых хищников с коэффициентом δ. С учётом этого получаем систему уравнений:
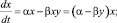
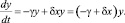(4)
В статье будет произведен обзор некоторых наиболее интересных моделей с применением системы дифференциальных уравнений Лотки – Вольтерры, с кратким авторским выводом по каждой из них.
«Динамическая городская модель Лотки – Вольтерры»
Это модель динамики развития популяции отношения городского населения к стране и отношения среднего дохода городского населения к среднестрановому, рассмотрена в работе D-J.F. Kamann и P. Nijkamp [3].
Население городов может представлять колеблющиеся паттерны в зависимости от их правильного использования экономии масштаба от экономической производительности города и от инкубационного потенциала. Авторы доказывают, что многие города США показывают стабильное динамическое поведение, похожее на спиралевидный путь, на основе использования двух ключевых переменных, выражающих городскую динамику: относительная популяция и доход на душу населения. Два дифференциальных уравнения, выраженных через отношение городского населения к национальному и отношение городского среднего дохода к среднему национальному доходу, показывают эволюцию популяции согласно модели Лотки –Вольтерры «хищник – жертва».
Модель выглядит следующим образом:
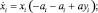(5)
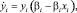
где i – зона рассмотрения; x – население; y – средний доход; a и β – динамические параметры.
Авторами были обнаружены различные интересные результаты по исследованию американских городов, которые подтверждают применимость модели Лотки – Вольтерры «хищник-жертва» для моделирования динамики городского населения. Главным достоинством модели является ее гибкость, выраженная в возможности генерировать широкий спектр динамического поведения городов, включая как стабильную, так и нестабильную динамику. Основным недостатком модели является недостаток экономических и статистических тестов, которые могли бы служить для более точной интерпретации результатов реализации модели. Также недостатком является отсутствие микроданных, безусловно влияющих на динамику городского населения и доходы населения [1], среди которых: предпринимательская активность жителей, различные программы стимулирования экономического роста муниципальными или федеральными органами.
Динамика конкуренции
на фондовой бирже на основе модели «хищник-жертва»
TheodoreModis [4] исследует конкуренцию на фондовой бирже, где существуют два вида конкуренции: между компаниями,
торгующимися на бирже, через их цену, а также между инвесторами, охотящимися за компаниями. Автор в исследовании для моделирования этих процессов также берет за основу систему уравнений Лотки – Вольтерры.
В рамках данной работы все акции на Нью-Йоркской фондовой бирже разделены на две группы или популяции: первая – это вся фондовая биржа как целое: несмотря на взаимосвязи с другими фондовыми биржами по всему миру, автор этой работы рассматривает Нью-Йоркскую биржу как отдельную нишу, где существуют свои правила, традиции и культура. В ней совершается более 80 % все фондовых транзакций в США, и это важнейшая фондовая биржа в мире. Вторая популяция – это индекс Доу-Джонс. 30 «голубых фишек», торгующих на Нью-Йоркской бирже, образуют свою микросистему внутри большой биржи. Они все подобны в некотором роде, иногда выражая себя как единственную альтернативу для потенциального инвестора. Также будет разумно предположить, что каждая из этих 30 компаний ведет себя на рынке как самостоятельное существо. Это подтверждается тем, что развитие индекса Доу-Джонс во времени подвержено собственному тренду движения на рынке, отличному от тех, которые образуют некоторые из «голубых фишек» в этом индексе за тот же период времени.
Преимуществом модели безусловно является глубоко проведенный анализ статистической информации по выявлению шаблонного поведения данных популяций, в разные исторические периоды. Это позволило TheodoreModis достаточно полно обосновать применимость модели Лотки – Вольтерры для моделирования рыночных процессов. Однако недостатком ее является отстраненность от фундаментальных причинразвития фондового рынка, с большой вероятностью влияющих на поведение моделируемых популяций.
Моделирование процессов
в банковской системе на основе модели
Лотки – Вольтерры
В данной модели автором AdrianComes [5] производится анализ банковской системы через аналогию с биологическими системами и применением трехуровневой системы дифференциальных уравнение Лотки – Вольтерры «хищник-жертва».
В экологических системах происходит передача энергетической биомассы от травоядных к хищникам и от растений к травоядным. Аналогично в банковской системе происходит трансфер капитала от Центрального Банка к обычным банкам и далее к частным лицам и компаниям (таблица).
В данном исследовании объектом изучения являются частные лица (поставщики/клиенты). Для имитации процессов в банковской системе используется трехуровневая модель Лотки – Вольтерры – система дифференциальных уравнений, анализирующих равновесие банковского сектора. Решением является идея найти динамическую точку равновесия в банковской системе методом Фоккера – Планка – Колмогорова.
Система дифференциальных уравнений данной модели выглядит следующим образом:
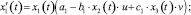
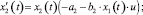(6)
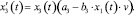
Так называемая трехуровневая модель Лотки – Вольтерры, рассматриваемая в этой работе, представляет собой систему уравнений по описанию передачи капитала в финансовой цепи. Главный хищник в ней – Центральный Банк, питающийся на обычных банках, которые он кредитует, а они, в свою очередь, питаются на финансовых ресурсах частных лиц и компаний. Автору удается найти некую точку в банковской системе путем нахождения оптимальных параметров математическими методами, при которой система приходит в равновесие и популяции мирно продолжают сосуществовать.
На наш взгляд, автором применен очень оригинальный подход к моделированию банковской системы, который, на первый взгляд, кажется вполне обоснованным с применением аналогий с биологическими системами. Однако автору недостает анализа реальных исторических данных по работе банковской системы, а также не учитывается при этом возможность эмиссии Центральным Банком денежных средств.
Экологическая система – финансовая система
|
Передача |
Уровень 1 |
Уровень 2 |
Уровень 3 |
|
|
Экологическая система |
Энергетическая биомасса |
Хищники |
Травоядные |
Растения |
|
Финансовая система |
Капитал |
Центральный банк |
Банки |
Частные лица и компании |
Модель замещения старых технологий новыми с использованием промежуточных технологий-связок
Автор данной работы AliAhmadian [6] применяет динамическое моделирование и систему уравнений Лотки – Вольтерры для моделирования замещения старых технологий новыми с участием так называемых «связующих технологий».
В данной системе три технологии взаимодействуют друг с другом. Новая технология E находится в прямой конкуренции со старой технологией M. Технология B – это другая, появляющаяся технология, находящаяся в отношении «хищник-жертва» с технологиями M и E. Технология B получает выгоду от существования технологии M, а технология E, в свою очередь, получает выгоду от развития технологии B.
Система дифференциальных уравнений для этой модели выглядит следующим образом:
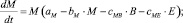
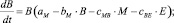(7)
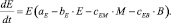
На рис. 2 представлены результаты реализации данной математической модели в компьютерной программе Mathlab с различными параметрами модели.
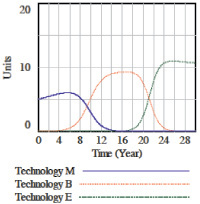
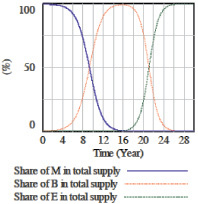
а б
Рис. 2. Симуляция модели конкуренции технологий [6]
Как можно увидеть из графиков имитации модели, технология B начинает поглощать технологию M из-за существования отношения «хищник – жертва» между ними. Как только технология M вымирает, технология E начинает пользоваться преимуществами от отсутствия старой технологии M и начинает получать выгоду от связующей технологии B. Следовательно, новая технология E в конце концов становится доминантной, а остальные технологии вымирают.
Таким образом, автор показывает важность существования связующей технологии, без которой новая технология не смогла бы занять рынок.
В данной работе производится достаточно детальный анализ различных типов поведения системы при разных параметрах. Также результаты, полученные путем реализации данной модели, позволяют сделать интересные выводы о роли переходных технологий – таких как гибридные двигатели, перед полным переходом на полностью экологически чистые двигатели. Как и во всех остальных моделях, данное исследование не имеет предварительного анализа реальных экономических данных для построения модели [2], а также не учитывает роль самого потребителя этих технологий, являющегося, на наш взгляд, основным локомотивом в развитии той или иной инновационной составляющей.
Выполнено в рамках научно-исследовательской работы по гранту Президента РФ для государственной поддержки молодых российских ученых по договору № 14.Z56.16.6249-МК от 14.03.2016 г.