Одной из важнейших задач современных систем управления является обеспечение гарантированного качества передачи информации с требуемой высокой скоростью [2]. Качество передачи характеризуется достоверностью – степенью соответствия переданных и принятых сообщений. Для цифровых систем передачи достоверность, оцениваемая вероятностью правильной передачи сообщения, должна быть достаточно близка к 1 [3].
Возможность обеспечения высокой достоверности обеспечивается несколькими составляющими [5]. Важную роль среди них играет помехоустойчивость – способность системы сохранять высокую достоверность при наличии помех в канале связи. Одним из основных способов обеспечения высокой помехоустойчивости является применение избыточных (корректирующих) кодов, способных корректировать ошибки на приемной стороне [6–9].
В современных системах управления применяются различные избыточные коды [3]: комбинаторные, алгебраические (групповые, циклические), арифметические и т.д. Большинство из них относятся к двоичным кодам и совпадают по размерности алфавита с первичными кодами, непосредственно кодирующими сообщения. Однако недвоичные коды показали более высокую эффективность применения по отношению к двоичным избыточным кодам. Одним из таких кодов является код Рида – Соломона, получивший широкое применение в системах передачи и хранения информации. Оно обусловлено высокой эффективностью (соотношением корректирующей способности и избыточности), превышающей соответствующие показатели аналогичных по размерности избыточных двоичных кодов (например, групповых или циклических). Поэтому исследование свойств кодов Рида – Соломона и возможностей их применения для помехоустойчивого кодирования информации в системах управления представляется важным и своевременным.
Краткая теория: принципы построения, кодирования и декодирования кодов Рида – Соломона
Коды Рида – Соломона [5] являются недвоичными кодами и представляют собой разновидность БЧХ-кодов, которые построены в поле Галуа по модулю q > 2 (GF(q)). Для иллюстрации формирования кода рассмотрим двоичную последовательность V длины M. Разобьем ее на блоки двоичных символов длины l. Количество блоков определяется как
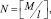
где [ ] – операция округления в большую сторону. Последовательность двоичных символов можно представить в виде полинома, коэффициентами Ei при переменной xi в котором будут символы недвоичного кода, отображающие блоки длины l:
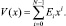(1)
Как известно, последовательность, состоящая из l двоичных символов, позволяет закодировать q = 2l. Таким образом, каждый блок представляет собой символ недвоичного кода Рида – Соломона (Р-С) и может быть представлен в виде полинома степени не выше m – 1 некоторой формальной переменной α:
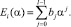
Полином, соответствующий символу кода Р-С, в поле Галуа GF(q) формируется по модулю некоторого полинома степени l, который должен быть неприводимым (делиться нацело только на 1 и самого себя) и примитивным (на него должен делиться нацело только полином степени не менее xq–1 + 1).
Код Р-С может быть записан в традиционной (n, m, d)-форме, параметры которой в большинстве случаев определяются следующим образом:
n = 2l – 1: общее количество символов кода,
k = 2s: количество дополнительных (избыточных) символов, s – кратность исправляемых ошибок,
m = n – k = 2l – 1 – 2s: количество информационных символов,
d = n – m + 1 = 2s + 1: минимальное кодовое расстояние.
Коды Р-С могут быть укорочены за счет уменьшения количества информационных символов или расширены, но не более чем до n = 2l + 1. Отметим, что при увеличении корректирующей способности s длина кода Р-С растет значительно медленнее, чем длина аналогичного БЧХ-кода, что позволит увеличить информационную скорость передачи (m/n).
Кодирование осуществляется аналогично двоичным БЧХ-кодам. Для этого необходимо построить порождающий полином g(x):
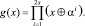(3)
Полином кода Р-С V(x) определяется как
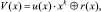(4)
где u(x) – информационный полином кода; r(x) – избыточный полином кода,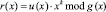 
. Деление может осуществляться либо в полиномиальном виде, либо в векторном виде по обычному алгоритму. Как известно, полином V(x) должен делиться на порождающий полином g(x) без остатка, что может быть использовано для проверки правильности вычислений.
Декодирование кодов Р-С, в отличие от двоичных БЧХ-кодов, имеет более сложный алгоритм. Это объясняется тем, что необходимо не только определить место ошибки, но и ее значение (в двоичных кодах для исправления достаточно инвертировать ошибочный символ). Незыблемым остается общий принцип – синдромное декодирование, основанное на вычислении полинома синдрома S(x) по принятому полиному V′(x) = V(x) ⊕ e(x):
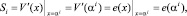
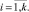(5)
Полином ошибки e(x) можно представить в виде
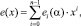
где коэффициент ei(α) показывает величину (вид) ошибки в i-м разряде.
Для определения мест возникновения ошибок, т.е. номера разрядов с ei(α) ≠ 0, строится полином локатора ошибок:
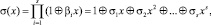(6)
где bi – номер локатора ошибки (номер ошибочного разряда i). Корнями полинома локатора ошибок будут величины 1/bi. Величины, обратные корням, будут показывать номера ошибочных разрядов. Для их определения можно построить следующее матричное уравнение:
(7)
В данном уравнении представим кратность исправляемых ошибок символом t. Все коэффициенты с индексами больше t равны 0.
Для определения коэффициентов si левая и правая части уравнения умножаются на обратную матрицу. Определив коэффициенты si, расположение ошибок определяется из n уравнений следующего вида: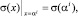 
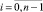. Если уравнение для αi обращается в ноль, значит, значение bi = 1/αi и покажет место ошибки.
По значениям степеней коэффициентов bj определяются номера ошибочных разрядов. Для определения значения ошибки ei(α) тоже строится матричное уравнение вида
(8)
Для определения коэффициентов ei левая и правая части уравнения умножаются на обратную матрицу.
Реализация лабораторного стенда
по исследованию кодов Рида ? Соломона в среде моделирования MATLAB
Изучение вопросов построения и реализации кодов Рида ? Соломона предлагается осуществить в рамках лабораторного практикума. Для этого разработан
и подготовлен виртуальный лабораторный стенд, реализованный в среде MatLab 7.0 разработки фирмы MathWorks Inc. Исследование традиционно состоит из двух частей: расчетной и практической (исследовательской).
В расчетной части необходимо выполнить расчет параметров кода по индивидуальным исходным данным, промоделировать работу кодирующего устройства, а также работу декодера в режиме исправления ошибок различного местоположения и кратности. В качестве исходных данных указываются: длина информационной части m, длина блока l, кратность исправляемых ошибок s, примитивный полином f(α), информационный полином u(x), варианты полинома ошибок e(x). В результате выполнения расчетной части необходимо рассчитать параметры кода, построить таблицу сложения, вычислить порождающий полином g(x), промоделировать работу кодирующего и декодирующего устройств.
Для облегчения процедур расчета разработаны и апробированы программные модули на встроенном языке программирования m-script [10], которые представляют собой необходимые макрофункции (умножения, деления, сложения по модулю и т.п., рис. 1). Они позволяют проверить правильность аналитического расчета и могут быть использованы как основа программной реализации процедур кодирования и декодирования (например, в микроконтроллерах, ПЛИС, вычислительных устройствах и других элементах систем управления).
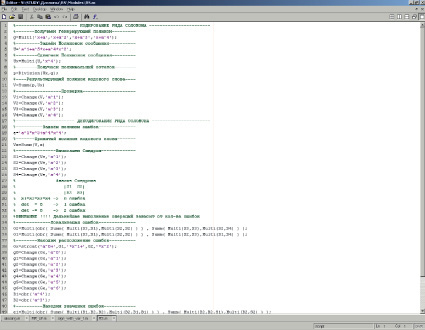
Рис. 1. Программные модули на языке m-script
В практической части сначала необходимо настроить параметры моделей кодирующего и декодирующего устройств (рис. 2, б), канала связи (рис. 2, в) в разработанной автором схемотехнической модели лабораторного стенда в среде моделирования Simulink (рис. 2, а).
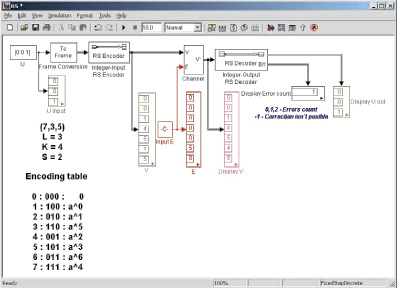
а
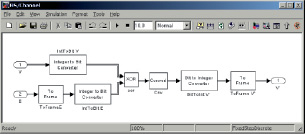
б в
Рис. 2. Модель системы, использующей коды Р-С, в среде Simulink
В результате выполнения практической части будет промоделирована работа кодирующего и декодирующего устройств, а затем выполнено сравнение результатов аналитического, программного и схемотехнического моделирование, а также анализ корректирующих свойств исследуемого кода.
Итогом выполнения предлагаемого исследования является закрепление теоретических знаний и получения практических навыков реализации современных методов помехоустойчивого кодирования, что важно для профессиональной подготовки специалистов в области систем управления [1, 4]. Навык реализации программной модели будет востребован на практике, поскольку разработанные алгоритмы реализации программного обеспечения могут найти применение в решении инженерных задач помехоустойчивого кодирования.
Заключение
Целью настоящей статьи является рассмотрение исследования современных методов помехоустойчивого кодирования информации. Был произведен аналитический обзор кодирования и декодирования избыточных недвоичных кодов Рида-Соломона, рассмотрены примеры основных процедур преобразования. Далее показаны основные подходы к реализации виртуального лабораторного стенда, построенного в среде моделирования MatLab, проиллюстрирована процедура их кодирования и декодирования.