Одним из важных условий при заключении договора страхования является своевременное извещение клиента страховой компании о страховом случае. Однако промежуток времени от наступления страхового случая до сообщения о нем страховщику в период, обозначенный в договоре, может выходить за пределы отчетного периода. В связи с этим для исполнения обязательств по таким претензиям страховщик наряду с резервами незаработанной премии, заявленных, но неурегулированных убытков и стабилизационным резервом формирует резерв произошедших, но незаявленных страховых убытков (далее – РПНУ) [6].
Согласно [9] РПНУ является оценкой обязательств страховщика по осуществлению страховых выплат, возникших в связи со страховыми случаями, произошедшими в отчетном или предшествующих ему периодах, о факте наступления которых в установленном законом или договорном порядке не заявлено страховщику в отчетном или предшествующих ему периодах. Обязанность формирования и методика расчета РПНУ предусмотрены страховым законодательством [6, 9].
В бухгалтерском балансе страховой компании РПНУ как обязательство страховщика перед клиентами входит в состав пассивов и оказывает влияние на налогооблагаемую базу, величину необходимых активов для обеспечения обязательств РПНУ, на расчеты с перестраховочными компаниями, тарифную политику, расчеты с акционерами, платежеспособность, финансовую устойчивость, убыточность и т.п. В связи с этим правильность и точность оценки РПНУ является существенным для страховщика. С одной стороны, завышенная оценка требует адекватного размера актива в покрытие резерва, с другой стороны, заниженная оценка может привести к нехватке средств на страховые выплаты и, следовательно, неплатежеспособности страховой компании.
Для расчета РПНУ наиболее широко применяются методы, основанные на использовании треугольников развития убытков (оплаченных или состоявшихся) – методы цепной лестницы, Борнхюттера – Фергюсона, Берквиста – Шермана, а также методы, основанные на ожидаемой убыточности [3–5, 7, 8].
В настоящей статье рассматривается стохастическая имитационная модель оценки резерва произошедших, но не заявленных убытков, в виде одноканальной системы массового обслуживания (на примере авиационного страхования и страхования средств наземного транспорта), описанная в семимартингальных терминах. В качестве статистических данных количества и размера произошедших убытков использовались данные «Страховой компании НИК» (далее – Компания) за период 2010–2015 г.
Стохастическое моделирование системы массового обслуживания проводилось в программной среде высокого уровня Microsoft Visual Studio 2010 на языке C#, оценки функций распределения по эмпирической выборке страховых возмещений – в среде Microsoft Excel 2010 и Statistica 10.0.
Постановка задачи
Рассмотрим одноканальную систему массового обслуживания в терминах точечных процессов [2]. Пусть процесс (At)t≥0 – точечный считающий процесс числа произошедших убытков в момент времени t ≥ 0, (Dt)t≥0 – точечный считающий процесс числа заявленных, но неурегулированных убытков (убытки, о которых известно компании на момент времени t), (Qt)t≥0 – число произошедших, но незаявленных убытков. Взаимосвязь этих процессов представлена в виде системы массового обслуживания (далее – СМО), в которой роль заявок играет наступление страховых случаев, длину очереди – процесс (Qt)t≥0, а количество обслуженных заявок – процесс (Dt)t≥0 (рис. 1). Тогда балансовое уравнение запишется в виде
Qt = Q0 + At – Dt, (1)
где A0 = 0; B0 = 0; D0 = 0.
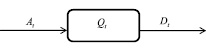
Рис. 1. Общая схема работы СМО
Процессы At, Dt, Qt рассматриваются на стохастическом базисе B(Ω, F, ? = (Ft)t≥0, P), где At, Dt – независимые пуассоновские процессы с интенсивностью λ > 0 и δ > 0 соответственно. В соответствии с разложением Дуба-Мейера для субмартингалов [2] процессы At, Dt могут быть представлены как
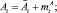
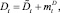(2)
где 
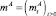и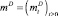 
– квадратично-интегрируемые мартингалы на B, а 
, 
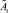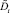– компенсаторы процессов
At, Dt вида
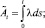
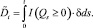(3)
Стохастическая имитационная модель расчета РПНУ может быть построена следующим образом.
Пусть ηt – размер убытка, заявленного клиентом в момент времени t, есть случайная величина с функцией распределения F(η ≤ x), тогда It – величина РПНУ в момент времени t – может быть определена как
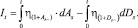(4)
Численный расчет количества произошедших, но незаявленных убытков
Для оценки параметров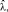 
введем следующие параметры: 
– дата i-го страхового случая, 
– дата уведомления об i-м страховом событии страховщику,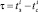 
– количество дней, исчисляемое от даты страхового случая до даты уведомления, 
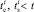, i = 1...N, где N – количество страховых случаев за рассматриваемый период.
Так как время между наступлениями страховых случаев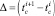 
имеет экспоненциальное распределение, то значение 
может быть вычислено методом максимального правдоподобия [5], как
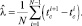(5)
Аналогично вычисляется значение интенсивности обслуживания как среднее количество дней между датами страхового случая и даты заявления об убытке:
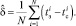(6)
На рис. 2–3 приведены иллюстративные примеры моделирования процесса At – количества произошедших убытков за период (0, T) по статистическим данным Компании для страхования средств воздушного транспорта (КАСКО ВС, N1 = 40) с оценочными параметрами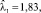 
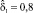и для страхования средств наземного транспорта (КАСКО АМ, N1 = 316) с параметрами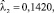 
.
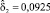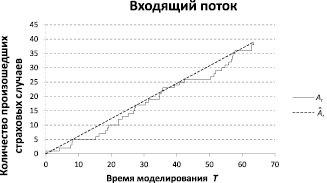
Рис. 2. График процессов At 
(КАСКО ВС), дискретность t = 1 месяц, T = 63 мес.
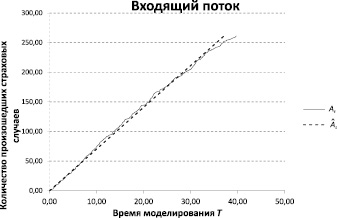
Рис. 3. График процессов At 
(КАСКО АМ), дискретность t = 1 месяц, T = 40 мес.
Математическая модель размера страхового убытка
Определим по эмпирической выборке η1, η2, ..., ηN страховых возмещений, функцию распределения случайной величины η в предположении, что для каждого вида страхования выборка страховых возмещений случайна и однородна.
Используя классический аппарат подгонки функции распределения по эмпирическим наблюдениям страховых возмещений, представленный в [4, 5, 7, 8], установим, что наиболее подходящей функцией распределения страхового возмещения для КАСКО ВС и КАСКО АМ (с точки зрения критерия Колмогорова-Смирнова) является логнормальное распределение с параметрами μ > 0, σ2 > 0 и плотностью вида
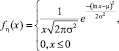x > 0. (7)
Параметры логнормального распределения по эмпирической выборке оценены методом максимального правдоподобия:
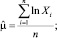
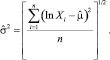(8)
Основные параметры оценки функции распределения, критерий Колмогорова − Смирнова
|
Вид страхования |
Объем |
Eη |
|
|
|
Критерий Колмогорова ? Смирнова |
|
КАСКО АМ |
316 |
5,6415?104 |
1,17?105 |
3,5016 |
0,93 |
0,068 |
|
КАСКО ВС |
40 |
5,8756?105 |
1,078?106 |
0,6635 |
1,5842 |
0,084 |
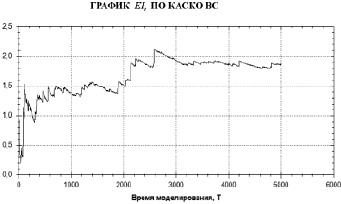
Рис. 4. График EIt, (в USD) для КАСКО ВС, t = 1 месяц, T = 5000
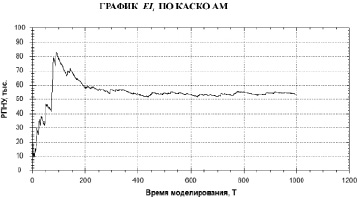
Рис. 5. График EIt, (в тыс. рублей) для КАСКО АМ, t = 1 месяц, T = 1000
Пример подгонки эмпирической функции распределения к теоретической представлен на рис. 4.
В предположении стационарности параметров λ, δ, μ, σ определим среднюю величину EIt при T → ∞ (время моделирования) по формуле
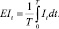(9)
Заключение
В настоящей статье была рассмотрена стохастическая имитационная модель резерва произошедших, но незаявленных убытков, построенная в терминах систем массового обслуживания. Для видов страхования КАСКО АМ и КАСКО ВС отдельно построена модель количества произошедших, но незаявленных убытков, а также определена функция распределения страхового возмещения в момент времени t.
Преимуществом использования настоящей имитационной модели расчета РПНУ является высокая степень адекватности реальным данным, что подтверждается графиками 2–6. Кроме того, применение настоящей модели не требует предварительного длительного процесса накопления данных об убытках и дискретизации страховых выплат (на квартал, полугодие, год) как этого требуют цепочно-лестничные методы.
Стохастическое моделирование системы массового обслуживания расчета РПНУ реализовано в среде Microsoft Visual Studio 2010 на языке C#. Подгонка функции распределения по эмпирическим данным страховых возмещений реализована в пакете Statistica 10.0.
Настоящая имитационная модель расчета РПНУ может быть усовершенствована в случае представления процессов At, Dt в виде мультивариантных процессов [2].