При моделировании структуры неупорядоченной среды успешно используются методы теории перколяции и теории фракталов. Простая задача теории перколяции имеет следующий вид: дана решетка, состоящая из проводящих и непроводящих узлов (распределение которых случайно), в которой p – концентрация проводящих узлов и (1 – p) – концентрация непроводящих узлов. Найти такую минимальную концентрацию p, при которой существует путь по проводящим узлам через всю решетку. Такую концентрацию p называют порогом перколяции (протекания). Свойства перколяционной системы кардинально изменяются при переходе через порог перколяции.
Теория перколяции имеет два основных направления исследований: геометрическое и физическое. Геометрическая часть теории перколяции исследует вопросы структуры, статистики, связности конечных и бесконечных кластеров в пространствах различной мерности, физическая часть теории перколяции исследует различные физические процессы. Перколяционные модели бывают решеточными и континуальными. Континуальные перколяционные модели позволяют получать более точные результаты исследования структуры и свойств неупорядоченных сред.
В настоящей работе исследована геометрическая структура неупорядоченной среды, которая представлена континуальной перколяционной моделью. Важным фактором при моделировании структуры неупорядоченных сред является равномерное распределение частиц. Исследователи используют различные генераторы случайных чисел для получения распределений частиц, и чаще всего полученные распределения даже не проверяются на равномерность или проверяются каким-либо одним стандартным способом математической статистики. Равномерность таких распределений остается под большим вопросом. Более того, до сих пор не существует универсального алгоритма диспергирования частиц, который гарантировал бы случайное равномерное распределение. В рамках рассмотренной модели предложены и исследованы два алгоритма диспергирования частиц. Первый алгоритм является стандартным и используется во множестве исследований, второй алгоритм предложен авторами настоящей работы впервые.
Материалы и методы исследования
При исследовании геометрической структуры неупорядоченной среды были использованы методы компьютерного моделирования, теории перколяции, теории вероятности и математической статистики.
Континуальная перколяционная модель неупорядоченной среды представлена в виде конечной системы, равномерно заполненной частицами. В роли частиц выступают сферы одинакового размера с радиусом r, упакованные в куб линейного размера L. Сферы пересекаться не могут. При моделировании использованы периодические граничные условия по всем трем направлениям. Для генерации случайных чисел – координат центров сфер – использован алгоритм «Вихрь Мерсенна», обладающий большим периодом, значения которого более чем достаточно для решения поставленной задачи [13]. Исследованы два алгоритма заполнения системы частицами. В рамках первого алгоритма генерируются поочередно три значения координат центра сферы. Если сгенерированная сфера не пересекается с ранее упакованными, то она принимается, иначе отвергается. Количество сфер определяется необходимым значением концентрации частиц неупорядоченной среды. В рамках второго алгоритма генерируются поочередно списки x-координат, y-координат и z-координат центров всех сфер. Далее из этих списков формируется структура, состоящая из непересекающихся сфер, количество которых также определяется необходимым значением концентрации частиц неупорядоченной среды. Если возникает ситуация, что из оставшихся координат не удается выбрать центр сферы, которая не пересекалась бы с ранее упакованными, то отвергается не три координаты, а одна, и генерируется новая. Если с вновь сгенерированной координатой также не нашлось нужной комбинации, генерируется вторая, потом третья и так далее, пока не будет достигнуто необходимое количество сфер. В обоих алгоритмах одинаковые критерии близости сфер, одинаковые параметры исследуемой системы, и задано максимальное число попыток упаковать очередную сферу, равное L×L×L (то есть предполагается, что если L×L×L раз подряд не удалось упаковать очередную сферу в куб, то свободного места для размещения элемента нет (явление джэмминг); можно было бы сделать это число еще большим, однако при увеличении числа попыток разница в количестве упакованных сфер не значительна, а временные затраты весьма значительны).
Так как выбор алгоритма диспергирования частиц является ключевым моментом при моделировании структуры неупорядоченной среды, то авторами было принято решение провести оценку равномерности полученного распределения сфер в кубе, используя пять критериев. Критерии включают в себя как оценку непосредственно закона распределения, так и проверку качества генератора псевдослучайных чисел: критерий χ-квадрат Пирсона [5]; второй способ основывается на том, что точки (центры сфер) считаются равномерно распределенными по некоторому объему VL, если в любом элементарном объеме 
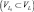 количество точек ni пропорционально величине этого объема [1]; третий способ основан на сведении трехмерной задачи к одномерной и включает в себя следующие действия (строится функция распределения среднего количества сфер от размера куба, где размер куба меняется от L/10 до L с шагом L/10 и по коэффициентам аппроксимирующей функции проводится оценка равномерности распределения сфер) [5]; четвертый способ проводит проверку генератора псевдослучайных чисел, используя оценку математического ожидания полученного распределения (генератор псевдослучайных чисел дает удовлетворительное распределение по заданному закону с вероятностью не менее 90 %, если рассчитанное в результате компьютерного моделирования математическое ожидание не отклоняется от теоретического, более чем на 10 %) [1]; критерий типа Колмогорова – Смирнова [6, 7].
количество точек ni пропорционально величине этого объема [1]; третий способ основан на сведении трехмерной задачи к одномерной и включает в себя следующие действия (строится функция распределения среднего количества сфер от размера куба, где размер куба меняется от L/10 до L с шагом L/10 и по коэффициентам аппроксимирующей функции проводится оценка равномерности распределения сфер) [5]; четвертый способ проводит проверку генератора псевдослучайных чисел, используя оценку математического ожидания полученного распределения (генератор псевдослучайных чисел дает удовлетворительное распределение по заданному закону с вероятностью не менее 90 %, если рассчитанное в результате компьютерного моделирования математическое ожидание не отклоняется от теоретического, более чем на 10 %) [1]; критерий типа Колмогорова – Смирнова [6, 7].
Основной проблемой при применении критерия Пирсона является выбор оптимального количества малых кубиков, на которые необходимо разбить рассматриваемый куб для достижения объективной оценки равномерности распределения (так называемое оптимальное число интервалов). По этой проблеме проводятся исследования [3, 4, 8–12, 14, 15]. Предложено несколько формул для нахождения оптимального числа интервалов, но ни одна из них научно не обоснована. Выбор какой-либо формулы для нахождения оптимального числа интервалов гистограммы стоит за исследователем и несет субъективный характер. Авторами настоящей работы было решено модифицировать формулу Скотта определения оптимального числа интервалов [14], которая является более или менее научно обоснованной, удовлетворяет некоторым требованиям в рамках предложенной перколяционной модели. Авторами была получена следующая модификация формулы Скотта:
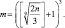 (*)
(*)
Результаты исследования и их обсуждение
При моделировании для обоих алгоритмов упаковки сфер были использованы следующие входные параметры: линейный размер куба L = 50, радиус сферы r = 0,5, количество сфер n варьировалось от 1000 (концентрация сфер составляет 0,42 %) до 60000 (концентрация сфер составляет около 25,13 %), количество испытаний k = 100 для каждого значения n, число интервалов m гистограммы для критерия Пирсона вычислялось по формуле (*). Соотношения размера сферы и куба достаточно для получения достоверных результатов, применимых для бесконечных систем. Также применимость результатов моделирования для бесконечных систем основывается на применении периодических граничных условий при моделировании. Выбор значения концентрации от 0,5 до 25 % для моделирования основывается на следующих факторах. Во-первых, порог перколяции для жестких сфер соответствует значению 30–34 % концентрации (разные исследователи получают различные значения порога), порог перколяции жестких сфер с проницаемыми оболочками меняется от 5–6 до 30–34 % в зависимости от толщины проницаемой оболочки. Интерес при исследовании структуры свойств неупорядоченных сред представляют именно допороговые и пороговые концентрации. Во-вторых, при заполнении системы свыше 30 % содержания сфер получаются довольно плотные упаковки, а свыше 40–45 % часто возникает явление джэмминга (явление, при котором пустоты еще есть, но их размера недостаточно для размещения очередной сферы). Таким образом, временные затраты на моделирование велики, а результаты моделирования не представляют особого интереса, так как после порога перколяции система слабо меняет свои свойства. Число испытаний, равное 100, является достаточным для получения адекватных статистических данных с точностью 0,05 и вероятностью получения данной точности 0,99 [1].
Основным результатом моделирования является полученная зависимость количества отвергнутых сфер от доли заполнения системы частицами для обоих алгоритмов диспергирования (рис. 1).
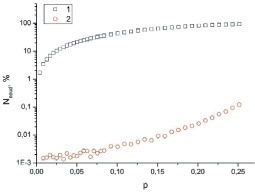
Рис. 1. Количество отвергнутых сфер при случайном распределении в куб при различных долях заполнения: 1 – первый алгоритм; 2 – второй алгоритм
На графике видно, что при первом алгоритме количество отвергнутых сфер растет значительно с увеличением доли заполнения и уже после 0,2 доля отвергнутых сфер превышает 90 %. Для второго алгоритма, наоборот, отвергается очень мало сфер и в рассмотренном диапазоне долей заполнений не превышает 1 %. Можно предположить, что распределение, полученное вторым алгоритмом диспергирования, удовлетворяет заданному закону распределения с большей надежностью, так как последовательность случайных чисел, представленная генератором, практически не меняется. Для доказательства данного предположения были проведены оценки равномерности распределения для обоих алгоритмов диспергирования. По критерию Пирсона получена зависимость отношения 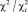 от доли заполнения системы сферами. Зависимость аппроксимируется функцией вида x(p) = Apb, где
от доли заполнения системы сферами. Зависимость аппроксимируется функцией вида x(p) = Apb, где 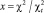 , и коэффициенты принимают значения, представленные в таблице. Если
, и коэффициенты принимают значения, представленные в таблице. Если 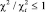 , то распределение можно считать равномерным с надежностью 0,99999 (
, то распределение можно считать равномерным с надежностью 0,99999 (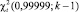 , где k – число интервалов гистограммы). По коэффициентам аппроксимирующих функций видно, что для обоих алгоритмов заполнения получены хорошие значения критерия, согласно которому полученные распределения удовлетворяют равномерному закону.
, где k – число интервалов гистограммы). По коэффициентам аппроксимирующих функций видно, что для обоих алгоритмов заполнения получены хорошие значения критерия, согласно которому полученные распределения удовлетворяют равномерному закону.
|
The first algorithm |
The second algorithm |
|
|
A |
0,0009 ± 0,0001 |
0,0021 ± 0,0003 |
|
b |
–0,31 ± 0,04 |
–0,14 ± 0,05 |
Согласно второму, третьему и четвертому критериям по результатам моделирования также можно утверждать, что оба алгоритма диспергирования дают распределения, удовлетворяющие равномерному закону с одинаковой надежностью.
Согласно критерию типа Колмогорова – Смирнова получена зависимость λ/λкр от доли заполнения системы частицами для обоих алгоритмов диспергирования, которая представлена на рис. 2 и 3. Полагается, что если λ/λкр ≤ 1, то выборка с отвергнутыми сферами и контрольная выборка принадлежат одному закону распределения (равномерного), иначе не принадлежат. По графикам видно, что при малых значениях доли заполнения оба алгоритма диспергирования показывают хорошие результаты. Однако с ростом доли заполнения первый алгоритм ведет себя значительно хуже. Количество точек, в которых первый алгоритм дает неудовлетворительное распределение приблизительно в два раза больше точек, в которых второй алгоритм дает, неудовлетворительное распределение (соотношение 18:10), причем в трех из десяти точек второго алгоритма отклонение от 1 менее чем на 10 %. Кроме того, значения отклонений от 1 у первого алгоритма диспергирования значительно превышают значения отклонений у второго алгоритма. Из этого можно сделать вывод, что по данному критерию предпочтительнее использовать второй алгоритм диспергирования. Критерий типа Колмогорова – Смирнова является одним из основных и наиболее широко используемых непараметрических методов, так как достаточно чувствителен к различиям в исследуемых выборках [6, 7]. Поэтому результаты оценки, полученные данным критерием, стоит считать наиболее достоверными.
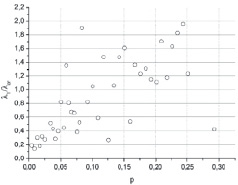
Рис. 2. Результаты двухвыборочной оценки распределения, полученного первым способом диспергирования, с помощью критерия типа Колмогорова – Смирнова
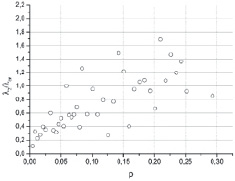
Рис. 3. Результаты двухвыборочной оценки распределения, полученного вторым способом диспергирования, с помощью критерия типа Колмогорова – Смирнова
Заключение
В настоящей работе были исследованы два алгоритма диспергирования частиц в неупорядоченной среде. В рамках первого алгоритма частицы, имеющие перекрытие с другими ранее распределенными частицами, отвергаются. В рамках второго алгоритма, для частицы, имеющей перекрытие с другими ранее распределенными частицами, ищется другое положение в среде, и если оно не найдено, то частица отвергается. Получены основные результаты:
1. Для обоих алгоритмов диспергирования частиц была получена зависимость количества отвергнутых сфер от доли заполнения системы частицами. При первом алгоритме количество отвергнутых сфер растет значительно с увеличением доли заполнения и уже после 0,2 доля отвергнутых сфер превышает 90 %. Для второго алгоритма, наоборот, отвергается очень мало сфер и в рассмотренном диапазоне долей заполнений не превышает 1 %.
2. Для обоих алгоритмов распределения были проведены оценки равномерности с помощью пяти критериев. По четырем критериям из пяти распределения, полученные обоими алгоритмами диспергирования, эквивалентны.
3. Критерий типа Колмогорова – Смирнова показал, что предпочтительнее использовать второй алгоритм диспергирования частиц.
Таким образом, структура неупорядоченной среды, полученная вторым алгоритмом диспергирования, более однородна, чем структура, полученная первым алгоритмом.
Работа выполнена при поддержке РФФИ (гранты РФФИ-ц № 15-01-07946-а, 14-08-96011 р_урал_а, 16-31-00064 мол_а).



