При изготовлении оболочек вращения осуществляется контроль формы поперечных сечений, как правило, измерением радиус-векторов i-тых точек поверхности. Отклонения формы 
определяются как
,
где:
радиус-векторы, измеренные в 
точках по периметру контролируемого сечения; 
, 
номинальный радиус поперечного сечения оболочки.
Отклонения приводятся к одной из принятых баз отсчета [1].
Такой контроль выполняется неоднократно на разных стадиях изготовления оболочек. При насыщении конструкции внутренними элементами некоторые точки становятся недоступными для контроля. В случае использования в качестве базы отсчета отклонений формы средней окружности, в методику расчета [2] необходимо ввести все 
значений отклонений. Как правило, значения отклонений в -тых точках недоступных для контроля получают линейным интерполированием смежных значений:
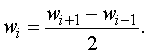
Такое решение допустимо, если количество точек контроля достаточно большое и значения отклонений на промежутке интерполирования изменяются по линейному закону. Однако, если отклонения в недоступных точках имеют экстремальное значение, то погрешность расчета может быть существенной. Более корректный результат можно получить, если использовать значения отклонений, полученные измерением на более ранних этапах контроля.
Обозначим отклонения формы, измеренные на стадии доступности измерений, через 
. Тогда можно записать:
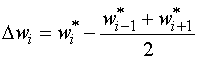, (1)
а отклонения в недоступной точке можно определить как:
. (2)
Основная предпосылка, положенная в основу решения, основана на том, что деформации оболочки, получаемые на поздних стадиях изготовления, имеют общий характер и практически не влияют на взаимное расположение близко расположенных точек. Такой подход позволяет получать удовлетворительные результаты и в случае, если недоступных точек две, и они расположены рядом. При этом значения отклонений в пропущенных точках и 
определяются по аналогии с формулами (1) и (2):
; (3)
; (4)
(5)
. (6)
Для количественной оценки погрешности методики, основанной на замене значений отклонений в недоступных точках средним смежных значений, были использованы результаты натурных измерений цилиндрических оболочек на двух стадиях изготовления. При этом все точки поперечного сечения были доступны для контроля, а «недоступность» на более поздней стадии создавалась условно.
Результаты численного моделирования показывают, что метод линейного интерполирования существенно влияет не только на значение отклонения в «пропущенной точке», но и на значения в ближайших точках. Величина погрешности при этом соизмерима с допуском на отклонения формы и существенно возрастает при увеличении количества недоступных точек.
Аналогичное моделирование выполнялось и с использованием предложенной методики. При этом рассматривались те же варианты недоступности одной, двух и четырех несмежных точек.
Многократные численные эксперименты подтверждает эффективность предложенной методики.
Необходимо также отметить, что решения (3) – (6) методики позволяют получить достаточно корректные результаты в случае, если недоступны для обмера две смежные точки. Решение нетрудно обобщить и на случай неравномерного расположения точек по периметру. При использовании других баз отсчета отклонений данная методика позволяет дополнить круглограмму, представленную в виде ряда чисел, восстановленными значениями отклонений в «пропущенных точках».
СПИСОК ЛИТЕРАТУРЫ:
- ГОСТ 24642-81. Основные нормы взаимозаменяемости. Допуски формы и расположения поверхностей. Основные термины и определения. Взамен ГОСТ10356-63; Введ. 01.07.81.- М.: Издательство стандартов, 1990. – 68 с.
- Свид-во об офиц. регистрации программы для ЭВМ. № 2002610926 «Krug-1» / Б.А. Новиков (RU). – № 2001611517; Заяв. 5.11.01; Опубл. 26.12.01, ОБ Роспатента “Программы для ЭВМ, базы данных, топологии интегральных микросхем” №1-2002.