В качестве первого приближения в теоретическом анализе процесса размерной электрохимической обработки (ЭХО) используется модель «идеального процесса». Основные постулаты модели и их подробное обоснование приведены в работе [2]. Согласно этой модели, электрическое поле в межэлектродном промежутке можно считать потенциальным, т.е. 
, где 
- вектор напряженности электрического поля, 
- потенциал электрического поля. В идеальном процессе ЭХО электрическое поле может быть описано уравнением Лапласа
. (1)
При соблюдении необходимых условий после длительного времени обработки, обрабатываемая поверхность принимает определенную постоянную во времени форму, которую называют установившейся или стационарной. В этом случае линейная скорость анодного растворения 
по нормали к поверхности анода в любой точке анода будет равна:
, (2)
где 
- выход по току для реакций анодного растворения металла, 
– плотность тока, 
- электрохимический эквивалент металла, 
- плотность материала анода, 
- угол между вектором 
скорости подачи катода и вектором 
внешней нормали к аноду [2]. Тогда установившееся распределение плотности тока 
на стационарной анодной границе определяется следующим равенством:
. (3)
В работе [3] установлена важная гидродинамическая аналогия задачи стационарного электрохимического формообразования и показана возможность применения теории обратных краевых задач для аналитических функций при исследовании плоскопараллельных задач теории электрохимического формообразования.
Рассмотрим плоскую задачу теории электрохимической размерной обработки металлов, состоящую в нахождении формы установившейся анодной границы, образующейся при обработке катодом-инструментом с криволинейным участком границы.
Используя гидродинамическую интерпретацию задачи [3], перейдем к исследованию соответствующего фиктивного течения идеальной несжимаемой жидкости. Рассмотрим плоское установившееся течение идеальной несжимаемой жидкости в части плоскости 
, ограниченной кривой 
, где 
, 
- полигоны, 
- криволинейная дуга, 
- свободная граница, скорость на которой определяется соотношением (2). Точкам полигонов 
, 
, в которых скачком меняется направление вектора скорости, соответствуют точки 
.
Введем вспомогательное комплексное переменное 
, изменяющееся в области 
- прямоугольнике со сторонами 
и 
. Пусть границам 
течения соответствуют границы 
прямоугольника и 
- вертикальные стороны, а 
- горизонтальные стороны прямоугольника.
Для решения задачи будем искать функцию 
, конформно отображающую прямоугольник 
на область течения. Чтобы построить , достаточно найти производную комплексного потенциала 
в плоскости переменной и функцию Жуковского [1]
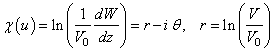, (4)
где 
- модуль скорости, 
- угол наклона вектора скорости к оси абсцисс, 
- значение скорости в точке 
. Затем с помощью параметрической зависимости
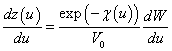. (5)
можно найти все необходимые геометрические характеристики течения, в частности, координаты точек свободной границы.
Функцию можно определить с помощью конформного отображения [4] области на область изменения комплексного потенциала , которая представляет полосу, полуполосу или прямоугольник в зависимости от наличия электроизолированных участков, линий симметрии. Если область изменения функции представляет полосу, производная 
легко определяется с помощью метода Чаплыгина [1].
Будем искать функцию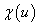 
в виде:
, (6)
где 
- функция Жуковского для фиктивного течения.
Функция 
удовлетворяет на границе области 
следующим условиям:
, 
,
, 
,
, 
,
, 
и легко находится [1].
Неизвестные функции 
находятся из решения краевой задачи, полученной при сравнении граничных условий для функций 
и . Далее используется методика, предложенная в работе [5].
В качестве примера решены две задачи обработки катодом – инструментом с криволинейным участком границы, в одной из которых катод имеет периодическую структуру.
СПИСОК ЛИТЕРАТУРЫ:
- Гуревич М.И. Теория струй идеальной жидкости. - Москва, 1961. – 536 с.
- Давыдов А.Д., Козак Е. Высокоскоростное электрохимическое формообразование. – Москва: Наука, 1990.- 272 с.
- Клоков В.В., Костерин А.В., Нужин М.Т. О применении обратных краевых задач в теории электрохимической размерной обработки.// Труды семинара по краевым задачам. Казань: изд-во КазГУ.-1972. - Вып. 9., С. 132-140.
- Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. - Москва: Наука, 1987. - 355 с.
- Котляр Л.М. Об одном случае струйного течения идеальной жидкости / Котляр Л.М.// Известия вузов. Математика. – 1976.- №2.