В строительстве, машиностроении, горном деле, а также в других отраслях материального производства зачастую применяются стержневые ажурные конструкции – фермы.
Они различаются большим многообразием геометрических размеров и схем, в том числе и по очертанию поясов, и по структуре стержневой решетки (взаимное расположение стоек и раскосов).
В процессе проектирования подобных конструкций имеется необходимость в изучении их напряженно-деформированного состояния – вычисление перемещений узлов и значений осевых усилий в стержнях.
В данной работе для решения таких задач использован метод конечных элементов для стержневых систем [1–8].
Экспериментальная часть
В качестве базового конечного элемента принят стержневой элемент фермы, произвольно ориентированный на плоскости (рис. 1).
Связь между величинами ui, zi имеет вид
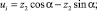
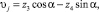(1)
или в матричной форме
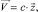(2)
где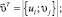 
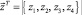; («Т» – индекс трансформирования);
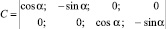(3)
– матрицы преобразований.
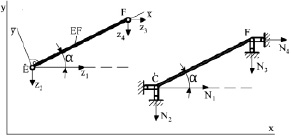
а б
Рис. 1. Конечный элемент стержневой системы: zi (i = 1, 2, 3, 4) – узловые перемещения в глобальной системе координат xy; Ni (i = 1, 2, 3, 4) – узловые силы; ui; νj (i = 1, 2; j = 3, 4) – узловые перемещения в локальной системе координат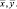 
На основе известных процедур метода конечных элементов (МКЭ) имеем
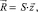(4)
где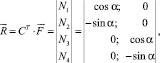 
или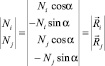 
(5)
– вектор узловых реакций в глобальной системе координат;
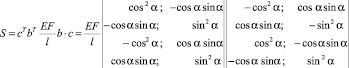(6)
– матрица жесткости стержневого конечного элемента в глобальной системе координат;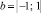 
– матрица деформации конечного элемента; «Т» – индекс трансформирования соответствующих матриц.
Представим выражение (5) в блочном виде
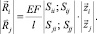(7)
Здесь: первый индекс элементов блока указывает на узел, в котором возникает соответствующая узловая реакция, второй индекс – номер узла, единичное смещение которого вызывает эти реакции.
По вектору 
продольная (осевая) сила в стержнях фермы определяется так:
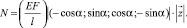(8)
Разрешающая система линейных алгебраических уравнений (СЛАУ) метода конечных элементов имеет стандартную форму
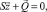(9)
где Sa·а – матрица реакций элементов, вызванных единичными перемещениями (матрица жесткости системы);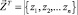 
– вектор неизвестных узловых перемещений заданной фермы; 
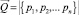– вектор узловых реакций, вызванных заданными внешними силами, при в узлах фермы (как в горизонтальном, так и в вертикальном направлении).
Учет опорных устройств (закреплений) заданной системы производится добавлением к диагональным элементам матрицы «S» значений жесткостных коэффициентов опор (их значения находятся в пределах 0–∞), т.е.
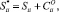(10)
где
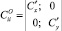(11)
– матрица коэффициентов жесткостей. При наличии жестких опор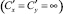 
при их отсутствии 
.
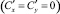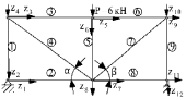
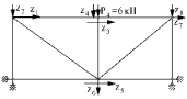
В качестве примера, иллюстрирующего предложенную выше методику расчета «МКЭ», рассмотрена плоская двухпанельная ферма с параллельными поясами (рис. 2) с шарнирными соединениями стержней в узлах фермы.
Далее приняты обозначения (рис. 2):
сβ = cos β; cα = cos α; sβ = sin β; sα = sin α;
сβ•sβ = cos β•sin β; сα•sα = cos α•sin α;
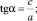
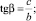
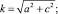
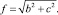(12)
Для рассматриваемой фермы (рис. 2) на основе уравнения (9) получена матрица жесткости системы.
Решение СЛАУ (9) дает значения искомых узловых перемещений zi (i = 1, 2, ..., 12)
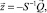(13)
где S–1 – обратная матрица.
Далее приведены результаты расчета фермы (рис. 2) при следующих конкретных значениях: a = b = c = 3,0 м; α = 45°; сα = Sα = cβ = Sβ = 0,71; k = f = 4,24.
В таблице даны значения узловых перемещений для ферм с различными схемами загружения.
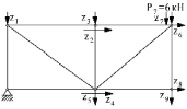
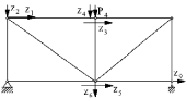
Для фермы № 4 (таблица) проведено исследование изменения величин узловых прогибов zi (i = 1, 2, 3). При Ра = 10 кН в зависимости от следующих факторов:
Рис. 3: при (а = b = 3 м = const); с = 2, 4, 6, 8, 10 м.
Рис. 4: при (с = 3 м = const); a = b = 2, 3, 4, 5 м (переменно).
Рис. 5: при (а = b = 3 м = const); p = 2, 4, 6, 8, 10 кН (переменно).
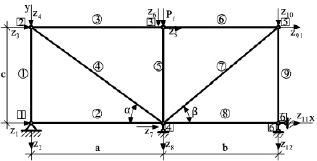
Рис. 2. Расчетная схема МКЭ: zi (i = 1, 2, ..., 12) – неизвестные узловые перемещения; Nj (j = 1, 2, ..., 9) – осевые усилия в стержнях фермы
Заключение
1. В данной работе доказана эффективность расчета стержневых конструкций методом конечных элементов. В качестве иллюстрационного примера рассмотрена плоская ферма с узловым нагружением.
2. Выполнено сравнение результатов численного расчета с классическим методом аналитического расчета ферм (определение усилий способом моментной точки, способом проекций, способом вырезания узлов). При этом установлено, что эти результаты совпадают без каких-либо погрешностей, т.е. решения будут точными.
3. Установлено, что разрешающие уравнения, представляющие собой матрицы различного порядка, эффективно реализуются на ЭВМ.
Результаты расчета различных ферм «МКЭ»
|
№ п/п |
Схема фермы с загружением узлов |
Расчетные величины |
|
|
Статически определимая ферма |
1 |
|
EFzi |
|
Ni, кН |
|||
|
2 |
|
||
|
Статически неопределимая ферма |
3 |
|
EFzi, (Р4 = 6кН) |
|
Статически определимая ферма |
4 |
|
Результаты исследований даны на рис. 3–5 |
Окончание таблицы
|
Номера расчетных величин (узлов или стержней) |
||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
1 |
0 |
0 |
9,091 |
9,091 |
0 |
61,364 |
0 |
43,182 |
–9,091 |
9,091 |
0 |
0 |
|
–3,03 |
0 |
–3,03 |
4,19 |
–6,06 |
–3,03 |
4,23 |
0 |
–3,03 |
– |
– |
– |
|
|
2 |
1,914 |
1,914 |
7,177 |
0 |
7,177 |
3,828 |
16,268 |
3,828 |
3,828 |
– |
– |
– |
|
3 |
4,396 |
2,198 |
2,198 |
17,417 |
0,382 |
12,257 |
–0,765 |
2,963 |
– |
– |
– |
|
|
4 |
Результаты исследований даны на рис. 3–5 |
|||||||||||
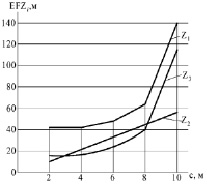
Рис. 3
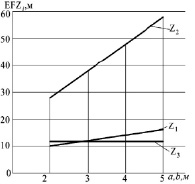
Рис. 4
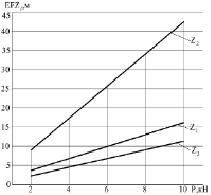
Рис. 5
4. Изменение размеров панелей a, b при постоянной высоте фермы «с» приводит к незначительному изменению значений перемещений z1, z3 (рис. 4).
5. Возрастание узловой нагрузки Р4 приводит к линейному изменению перемещений узлов фермы (рис. 5).
6. Изменение высоты фермы «с» при (a, b = const) линейно увеличивает значения z2, и нелинейно – z1, z3 (рис. 4).