Численное решение нелинейной двухточечной граничной задачи актуально для разделов оптимального управления, вариационных задач, астрофизики, биологии [5]. К основным методам решения относится сведение двухточечных задач к одноточечным задачам Коши с помощью конечно-разностных схем [6]. Излагаемый ниже метод отличается от известных по построению и тем, что дает непрерывное и непрерывно дифференцируемое компьютерное приближение решения двухточечной задачи. Метод основан на варьируемом кусочно-интерполяционном приближении решения задачи Коши для обыкновенных дифференциальных уравнений (ОДУ) с итерационным уточнением [9, 10]. Теоретические аналоги содержатся в [1, 2, 4], сходные эксперименты описаны в [11, 12]. В отличие от аналогов, предлагаемое итерационное уточнение строится на каждом подынтервале с помощью первообразной от интерполяционного полинома Ньютона, аппроксимирующего функцию правой части. Интерполяционный полином на подынтервале преобразуется к виду алгебраического полинома с числовыми коэффициентами, что обеспечивает табличную первообразную и позволяет программировать последовательность интегральных приближений Пикара. Для решения двухточечной задачи данный метод строится одновременно от начальной точки по направлению конечной и от конечной – к начальной. В окрестности точки пересечения встречные приближения интерполируются с применением итерационного уточнения. В результате в один проход получается непрерывное и непрерывно дифференцируемое кусочно-интерполяционное решение двухточечной задачи с точными значениями в начале и в конце промежутка.
Пусть вначале рассматривается задача Коши для ОДУ,
y′= f(x, y); y(x0) = y0, (1)
предполагается, что в области
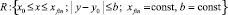
функция f(x, y) определена, непрерывна, непрерывно дифференцируема (в точках x0 – справа, xfin – слева), удовлетворяет условию Липшица: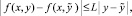 
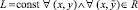. Предполагается также, что решение задачи (1) существует и единственно во всей R.
Варьируемое кусочно-интерполяционное приближение
Пусть F(x) – действительная функция одной действительной переменной, x ∈ [α, β], ε > 0 – априори заданная граница абсолютной погрешности. Строится объединение подынтервалов равной длины:
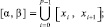P = 2k, k = 0, 1, ... (2)
На каждом подынтервале строится интерполирующий F(x) полином Ньютона Ψin(t) степени n с отстоящими на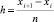 
узлами, n выбирается одинаковым для всех подынтервалов и минимальным при условии
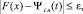x ∈ [xri, xri+1],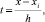 
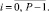(3)
Интерполяционный полином
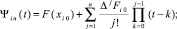
(4)
где xij = xi + jh – узлы интерполяции,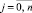 
; ΔjFi0 – конечная разность j-го порядка, преобразуется к виду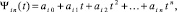 
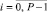. Для этого вычисляются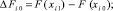 
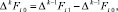
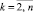, полагается bij = ΔjFi0, 
. Полином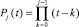 
разложен по корням k = 0, 1, ..., j – 1, находятся его коэффициенты:
(5)
Пусть zl = l,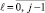 
. Для любых корней zl коэффициенты (5) дает формула [7, 8]
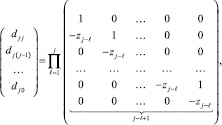
где k-й шаг умножения матриц справа налево записывается в виде
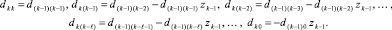(6)
Здесь
,
, 
.
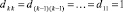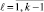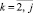При k = j левые части (6) совпадут с коэффициентами (5). После преобразований интерполяционный полином примет вид
(7)
где ai0 = F(xi0),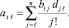 
Проверка точности приближения (3) полиномом (7) выполняется на каждом подынтервале в точках, равноотстоящих на h/γ, γ ≥ 3 – параметр. Для x ∈ [xi, x i+1) адрес выборки соответственных коэффициентов (7) даст i = [(x – α)/ρ], ρ = x i+1 – xi, 
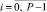. Построение полинома начинается от n = 1 при k = 0 для каждого i из (2), P = 2k, с проверкой (3) во всех проверочных точках. При нарушении (3) хоть в одной из них значение k увеличивается на единицу, так продолжается до априори заданной границы k ≤ k0. Если в результате искомая точность приближения не достигнута, то полагается k = 0, при этом n увеличивается на единицу, и так – до априори заданной границы n ≤ n0. Фиксируется наименьшее n, при котором (3) верно во всех проверочных точках всех подынтервалов, в соответствии с этим фиксируется k [7, 9].
Подобным способом аппроксимируется f(x, φ(x)) из (1), где y ≈ φ(x). Вначале в правую часть вместо y подставляется y0. Функция f(x, y0) приближается полиномами вида (7) по изложенной схеме так, как если бы F(x) равнялась f(x, y0). При фиксированных на выходе алгоритма n и k на подынтервале [xi–1, xi], i = 1, аналогично, при i = 2, 3, ..., выполняется итерационное уточнение. Первообразная
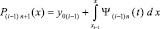
в виде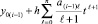 
принимается за приближение решения на данном подынтервале: 
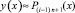. Полагается 
, при той же степени n на том же подынтервале строится аппроксимирующий полином (4) в форме (7):
.
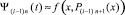Снова берется первообразная с тем же значением константы
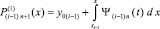
в виде 
, подставляется в правую часть,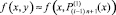 
, которая аппроксимируется аналогично:
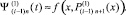
Итерации
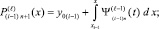
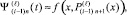l = 1, 2, ...,
где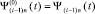 
, продолжаются до достижения заданной малости невязки, при реализации l ≤ q = const, t из (3).
Весь отрезок решения задачи (1) разбивается на отрезки равной длины:
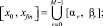
α r+1 = βr,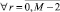 
, (8)
каждый отрезок [αr, βr] обрабатывается как [α, β] из (2), аналогично (2) рассматривается
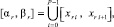
r = 0, 1, ..., M – 1, P = 2k, k ∈ {0, 1, ...}. (9)
За начальное значение на левой границе подынтервала [xri, xri+1] всегда принимается конечное значение на правой границе предыдущего подынтервала [xri–1, xri]: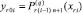 
, i = 1, 2, ..., P – 1, аналогично, при переходе от [αr, βr] к [α r+1, βr+1].
Пусть произвольно выбрано n, 1 ≤ n ≤ n0, n0 = const. Предполагается, что f(x, y(x)) имеет n + 1 непрерывную производную в R. Обозначим 
, где 
– приближение y(x) с помощью полинома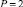 
. При P = 1, i = 0, [xr0, xr1] = [αr, βr], погрешность приближения полиномом (4), обозначаемым Ψr0n(t), оценивается из неравенства [3]:
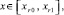(10)
где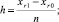 
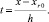Оценка соответствует k = 0 в (9), что интерпретируется как 0-й этап разбиения αr, βr]. Из (10) следует [9, 10]:
P = 1, [αr, βr] = [xr0, xr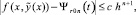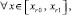1], 
(11)
где 1 ≤ n ≤ n0,
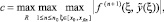c = const. (12)
Если P = 2, и на каждом из подынтервалов [xr0, xr1], [xr1, xr2] разбиения (9) выполняется интерполяция полиномом (4) с тем же значением n, то с учетом равенства числа узлов, отстоящих друг от друга на каждом подынтервале на h/2, получится аналог соотношения (11) с вдвое меньшим h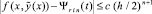 
, i = 0, 1. В общем случае [9] –
P = 2k; 
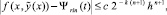
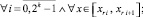
h – шаг интерполирования полинома Ψr0n(t) на [αr, βr] при k = 0. В предположении h < 1,
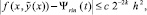
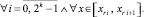
Пусть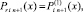 
x ∈ [xri, x ri+1]. Для приближения y(x) показано [10], что
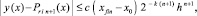
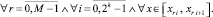(13)
Равномерная по n оценка получится, если учесть, что 1 ≤ n, и выбрать h < 1:
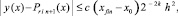
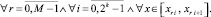(14)
В рассматриваемых условиях имеет место теорема 1.
Теорема 1 [9, 10]. При любом n, 1 ≤ n ≤ n0, n0 = const, последовательность полиномов Prin+1(x), где i из (9), r из (8), равномерно на [x0, xfin] сходится к решению y(x) задачи (1) при k → ∞. Скорость сходимости оценивается из (13), где c из (12), h – расстояние между узлами полинома Ψr0n(t), интерполирующего правую часть (1) на [αr, βr]. Значение h не зависит от r и не меняется с ростом k при разбиении данного отрезка на 2k подынтервалов. При h < 1 скорость сходимости оценивается как из (13), так и из (14).
В частности, теорема верна в случае двукратной непрерывной дифференцируемости правой части (1).
Следствие 1 [10]. В тех же условиях последовательность полиномов Ψrin(t) равномерно на [x0, xfin] приближает производную y′(x) при k → ∞ с оценками:
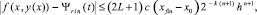
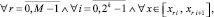
и если h < 1, то, в частности,
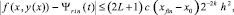
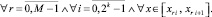
На практике вариации n, 1 ≤ n ≤ n0, и k, 1 ≤ k ≤ k0, реализуются по минимуму невязки так, чтобы дробь 2–k(n+1) оказалась наименьшей за счет произведения k(n+1).
Итерационное уточнение
Вначале на отрезке [αr, βr] выполняются вариации, на основе которых выбираются и фиксируются степень полиномов n, а также количество подынтервалов 2k. Затем на каждом подынтервале [xri, xri+1], i = 0, 1, ..., 2k – 1, выполняется итерационное уточнение:
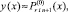
где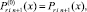 
x ∈ [xri, x ri+1];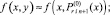 
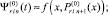
(15)
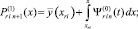
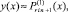
где q – конечный номер итераций на подынтервале
[xri–1, xri],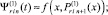 
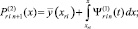
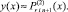
При l ≥ 2:
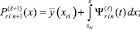
(16)
Обозначение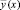 
вводится для отличия от 
, относительно которого итерационное уточнение не предполагалось. Итерации (15), (16) продолжаются до некоторой фиксированной границы l = q. Абстрактно допускается l → ∞. Показано [10], что если
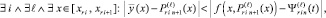(17)
то
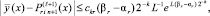
(18)
где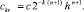 
Если же
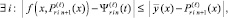
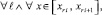(19)
то на этом подынтервале
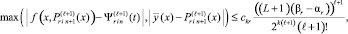
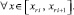
В условиях (19) итерационное уточнение снижает погрешность кусочно-интерполяционного приближения к решению и его производной пропорционально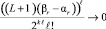 
при l → ∞, где L – константа Липшица. При условии (17) уменьшение погрешности ckr в (18) имеет коэффициент меньший единицы, если 
.
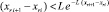Структура невязки
На отрезке [xj, x] фиксированной длины, x – xj << βr – αr, невязку можно представить в виде
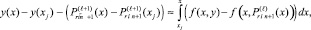
где 
и i – переменные значения индекса подынтервала, включающего x. Определяется разность аналогичных приближений для текущего и предшествующего количества подынтервалов:
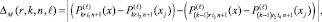(20)
где M из (8); i1, i2 – индексы соответственно конечного и начального подынтервалов, которым принадлежат x и xj в случае 2k подынтервалов в (9). По определению,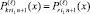 
для 2k подынтервалов, аналогично для – i2, 
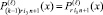для 2 k–1 подынтервалов, аналогично – для i4; для случая 2k–1 подынтервалов i3, i4 – номера конечного и начального подынтервалов, соответственно включающих x и xj на отрезке [αr, βr]. Отрезки [xj, x] покрывают [αr, βr]. Для начальной пары фиксированных n и k на объединении (9) находится и запоминается наибольшее ΔM(r, k, n, l), обозначаемое ∇M(r, k, n, l). Поиск ∇M(r, k, n, l) возобновляется при том же n и возрастании k на единицу в пределах 
, затем при увеличении n на единицу от начального k,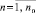 
, и т.д. Среди таких максимумов определяется минимальный по всем k и n:
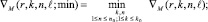
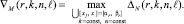(21)
В соответствии со значением ∇M(r, k, n, l; min) фиксируется 2k и n в границах [αr, βr]. В программной реализации минимум (21) определяется с итерационным уточнением полиномов в (20) при некотором l = const. Для соответственно зафиксированных k и n заново выполняется окончательное итерационное уточнение. Наибольшая точность и устойчивость метода относительно вида задачи достигается со следующей невязкой [10]:
.
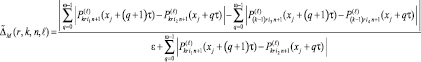Здесь ω – постоянное целое, выбранное экспериментально: ω = 5; ωτ – фиксированная часть длины [αr, βr], в случае 1 << βr – αr экспериментально выбранная как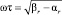 
. В случае жестких задач βr – αr < 1, и 
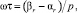p ≥ 2. Знаменатель нормирует невязку, ε > 0 – наименьшее число для исключения деления на ноль. С 
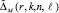выполняется то же, что с ΔM(r, k, n, l), для выбора 
, определяемого аналогично ∇M(r, k, n, l; min).
Случай системы ОДУ
Рассматривается задача
Y′ = F(x, Y); Y(x0) = Y0, (22)
где F(x, Y) = (f1(x, Y), f2(x, Y), ..., fN(x, Y)); Y = (y1(x), y2(x), ..., yN(x)); Y0 = (y01, y02, ..., y0N). Здесь и ниже F обозначает вектор-функцию N + 1 переменных в отличие от обозначения функции одной переменной в (3), (4). Используется 
Предполагается, что в области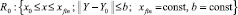 
выполнены условия существования и единственности, функция F(x, Y) определена, непрерывна и непрерывно дифференцируема, удовлетворяет условию Липшица:
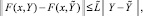
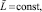
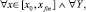
Кусочно-интерполяционное приближение и итерационное уточнение строятся для каждого уравнения системы (22) в полной аналогии случаю одной переменной. Здесь и ниже приближения всех компонентов на шаге рассматриваются при одних и тех же значениях l, k, n одновременно во всех уравнениях системы. Если правая часть (22) (n + 1)-кратно непрерывно дифференцируема в R0, то при каждом 
выполнено [10]:
x ∈ [xr0, xr1],
где Ψjr0n(t) – интерполяционный полином Ньютона в форме с числовыми коэффициентами, построенный для аппроксимации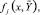 
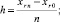
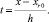Отсюда следует
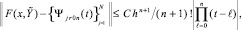x ∈ [xr0, xr1], (23)
где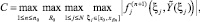 
C = const,
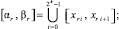
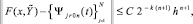
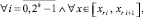(24)
h – шаг интерполирования полинома Ψjr0n(t) на [αr, βr] при k = 0, одинаковый для всех k = 1, 2, ... и для всех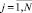 
. В предположении h < 1, –
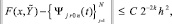
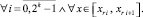(25)
На основе (23)–(25) получаются следующие оценки [10]:
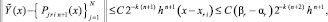
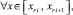
где P jrin+1(x) – первообразная от Ψjr0n(t), приближающая j-ю компоненту решения, при ограничении n ≤ n0, n0 = const,
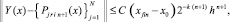
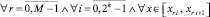
и, в предположении h < 1, –
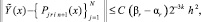
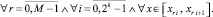
Отсюда следует равномерная сходимость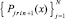 
к Y(x) на [x0, xfin]. С данными оценками формулируется аналог теоремы 1 для системы (22). Доказывается [10], что 
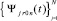равномерно на [x0, xfin] приближает производную Y′(x) при k →∞ с оценками:
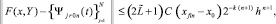
и, при h < 1,
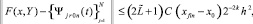
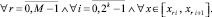
Итерационное уточнение
На [αr, βr] выполняются вариации, на основе которых выбираются и фиксируются степень полиномов n и количество подынтервалов 2k, затем на каждом подынтервале [xri, x ri+1], i = 0, 1, ..., 2k – 1, выполняется итерационное уточнение:
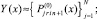
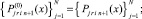
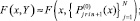
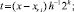
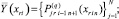
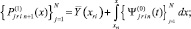
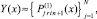
где q – конечный номер итераций на предыдущем подынтервале [xri–1, xri]. Далее,
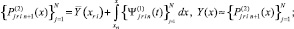
Если
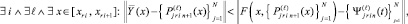
то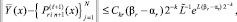 
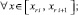
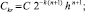(26)
если же
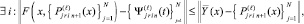
l = 0, 1, ...,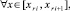 
то [10]
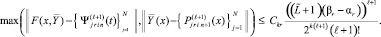(27)
Согласно (26), (27) итерационное уточнение уменьшает погрешность кусочно-интерполяционных приближений решения задачи (22) аналогично одномерному случаю.
Варьируемое кусочно-интерполяционное приближение решения двухточечной задачи Коши для системы ОДУ
Двухточечная задача Коши для системы (22) на отрезке [x0, xfin] ставится в виде
Y′ = F(x, Y); Y(x0) = Y0; Y(xfin) = Yfin,
где Y, F(x, Y) – те же, что в (22), Y0 = (y01, y02, ..., y0N); Yfin = (yfin1, yfin2, ..., yfinN). Для ее решения отрезок [x0, xfin] делится на две части, примерно, возле середины:
.
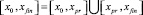На отрезке [x0, xpr] задача решается в точности описанным выше способом (движение вдоль этого отрезка обозначается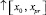 
). На отрезке [xpr, xfin] решение задачи выполняется в полной аналогии с предыдущим, однако за вектор начальных значений принимается (Y(xfin) = Yfin, и от точки xfin движение решения идет в обратном направлении – к xpr (движение в обратном направлении обозначается 
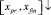). Обратное направление реализуется отрицательным значением шага –h во всех конечных разностях, построенных от xfin как от начальной точки, в каждом интерполяционном полиноме Ньютона на каждом подынтервале. Итерационное уточнение также строится в обратном направлении и имеет вид
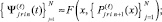
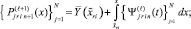
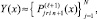
где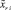 
– правый конец подынтервала и 
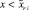. Этих изменений достаточно для получения кусочно-интерполяционного приближения на 
с теми же свойствами и с той же точностью, как в прямом направлении [10]. Приближения решения и его производной склеиваются на 
и на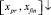 
в точке xpr с помощью интерполяционного полинома Ньютона той степени, которая получена на правой границе xpr по направлению вдоль 
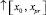. При этом часть узловых значений заимствуется слева от xpr, часть – справа от этой точки на 
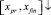. Полученный полином подвергается итерационному уточнению. Метод реализует программа [10], результат работы которой ниже приводится для задачи
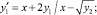
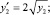y1(1) = 2; y2(1) = 4, .... y1(512) = 262656; y2(512) = 263169:
|
1.00, 6.12, … , 26.60, 31.72, 36,84, … , 509.44, 5.12 |
|
0.00, 0.00, , … , 0.00, 1.11×10–16, 0.00, …, 0.00, 0.00 |
В первой строке – значения независимой переменной, во второй – соответственная норма абсолютной погрешности приближенного решения. Точность приближения сравнима с точностью изложенного метода для соответствующих одноточечных задач Коши. Программы, эксперименты, доказательства приведенных утверждений приведены в [10].
Заключение
Компьютерный метод приближенного решения одноточечной и двухточечной задач Коши для ОДУ дает аналитическое приближение решения и его производной на основе кусочной интерполяции путем соединения узлов на смежных границах подынтервалов и задания в них равных узловых значений. С ростом числа подынтервалов метод равномерно сходится к решению, одновременно равномерно приближается производная. Скорость сходимости обратно пропорциональна числу подынтервалов. На основе преобразования интерполирующих решение и производную полиномов к алгебраическому виду с числовыми коэффициентами выполняется итерационное уточнение по типу последовательных приближений Пикара. Достигается сравнительно высокая точность приближения решения и производной для жестких и нежестких задач [10].