Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Математическая теория банков и банковской деятельности к настоящему времени приобрела вполне законченный вид, а инструментарий моделей и методов управления банковским портфелем весьма разнообразен. Однако большинство моделей относятся к «частным» моделям, ориентированным на решение конкретной задачи планирования и управления портфелями активов и пассивов. Решение комплексной задачи оптимизации этих портфелей с учётом фактора ликвидности и приоритетов кредитной политики банка в сфере ценообразования и отношения к риску требует использования «полных» моделей.

Предложенная ниже модель в полной мере может быть отнесена к «полным», т.к. отражает основные закономерности финансовых потоков банка по активно-пассивным операциям: первый уровень – мониторинг денежных потоков, генерируемых портфелем; второй уровень – взаимодействие портфеля активов с портфелем банка в целом.

Перейдём к описанию структуры и элементного состава экономико-математической модели мониторинга кредитного портфеля коммерческого банка (модель первого уровня).

Модели динамики банковских ресурсов, базирующиеся на непрерывном времени, весьма неудобны с позиции практической реализации. Во-первых, они предъявляют высокие требования к массивам данных, необходимых для их тестирования и адаптации, а во-вторых, «физическое» время, как правило, не соответствует внутренним ритмам «жизненного цикла» субъектов социально-экономических отношений.

Для перехода от непрерывного времени к дискретному, адекватно учитывающему условия деятельности финансово-экономических институтов, может быть использована интертемпоральная модель Дж. Хикса [5], в которой конечный отрезок времени [tн, tк] наблюдения исследуемой системы разбивается на равные интервалы длиной Δ:

[tн, tн + Δ), [tн + Δ, tн + 2Δ), …, [tн + (N – 1)•Δ, tк],

где 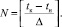Заметим, что все интервалы, кроме последнего, являются открытыми справа.

Данное разбиение предполагает, что внутри интервала [tн + (k–1)•Δ, tн + k•Δ) все параметры состояния банка, внешние и внутренние условия его функционирования являются постоянными и изменяются лишь при переходе через границы очередного временного промежутка.

Отрезки Δ одинаковой длины, на которые разделён временной интервал, назовём модельными периодами (месяц, день или часть дня). Выражение «момент времени» будет означать (если не оговорено иное) номер модельного периода. В тех случаях, когда двоякое толкование исключено, модельный период будем называть «периодом».

Сделаем следующие допущения: банк не оказывает существенного влияния на финансовый рынок (не относится к крупнейшим, системообразующим банкам); банк при проведении кредитно-депозитарной деятельности зависит только от решений собственников; на протяжении рассматриваемого интервала функционирования банк сохраняет статус и состав операций [1, 7].

В качестве типовых денежных потоков (притоков и оттоков) в модели кредитного портфеля присутствуют потоки от операций по поступлению денежных средств от размещённых кредитов, размещению денежных средств в кредиты, погашению обязательств.

Исходя из сделанных допущений, в модели среднерыночные процентные ставки и доходность определяются совокупным спросом и предложением всех банков, поэтому банк принимает сложившиеся на рынке процентные ставки и доходность и, отталкиваясь от них, определяет процентную политику операций [2].

Модель мониторинга кредитного портфеля банка учитывает следующие параметры потока средств банка, генерируемых активно-пассивными операциями, и особенности его регулирования: объём размещённых средств, объём процентных поступлений, своевременность и полнота возврата основного долга по кредитам, объём привлечённых средств, процентные расходы по привлечённым средствам, ликвидность портфеля, выполнение внешних и внутренних нормативов.

Введём следующие переменные:

t, τ – индексы модельных периодов на рассматриваемом интервале [0, T];

N(t) – количество выданных и незакрытых кредитов на период t (n – индекс кредита);

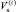– объём кредита с индексом n на период t;

V^(t) – объём кредитного портфеля банка на период t;

Y^(t) – объём погашений (поток платежей) по ранее размещённым кредитам на период t;

υ^(t) – доля плановых платежей на период t;

ρ^(t) – доля от суммы просроченных платежей по ранее размещённым кредитам, уплаченная на период t;

α^(t) – доля от суммы просроченных платежей по выданным кредитам, списанная в течение периода t (ввиду бесперспективности взыскания);

P^(t) – сумма просроченных платежей по выданным кредитам на период t;

β^(t) – доля основного долга по кредитам, погашенного в периоде t;

O^(t) – стоимость обеспечения выданных кредитов на период t;

k^(t) – коэффициент коррекции стоимости обеспечения в соответствии с реализованным обеспечением по неисполненным кредитам в периоде t;

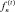– процентная ставка по текущему кредиту на период t.

Модель мониторинга и оценки активов банка для периода t включает следующие уравнения баланса в терминах введённых выше переменных:

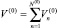(1)

(объём кредитного портфеля на нулевой период);

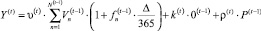(2)

(поток платежей по выданным кредитам, включающий средства, возвращённые в соответствии с графиком платежей, компенсацию за невозвращённые средства за счёт реализации залога и просроченные платежи, поступившие в текущий период);

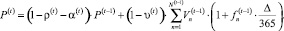(3)

Контроль качества кредитного портфеля банка на модельном интервале t предлагается осуществлять с применением коэффициентов k1 – k7, основным из которых на этапе мониторинга портфеля является коэффициент k2 просроченных ссуд – невозврата основной суммы долга – отношение просроченной задолженности к величине кредитного портфеля:

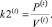(4)

Допустимой считается доля просроченной задолженности в кредитном портфеле менее 5 %, критической – 15 % [4]. В банковской практике пороговое значение 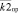коэффициента устанавливается на основе внутренних нормативов банка.

С учётом порогового значения 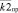коэффициента невозврата основной суммы долга получим следующее актуальное для периода tего превышение:

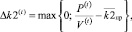(5)

которое следует учесть при формировании кредитного портфеля на следующем модельном интервале.

Модель второго уровня предназначена для выбора параметров кредитного портфеля банка на следующем интервале планирования (в первую очередь инвестируемых в кредиты средств банка) на основе обеспечения ликвидности временной структуры активов-пассивов.

Пусть M^(τ) – число вновь возникших обязательств банка в периоде τ; m = 1, …, M^(τ) – индекс депозита; 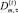– объём обязательств по депозиту с индексом m (проценты (в каждом текущем периоде) и основная сумма (в конечном периоде)), заключённому в период τ, на модельный период t. Тогда требуемая ликвидность L(t) портфеля депозитов банка на период t₀ может быть оценена величиной

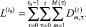(6)

Ограничениями модели взаимодействия портфелей активов и депозитов банка выступают требования по погашению обязательств полностью и в срок (требования ликвидности). Однако согласовать потоки погашений обязательств и потоки платежей по выданным кредитам «без зазоров» не представляется возможным. Напротив, реально согласовать эти потоки, обеспечив опережающий возврат средств от кредитов.

Исходя из этой предпосылки, рассмотрим стратегию кредитования, ориентированную на рост согласованности временной структуры активов-пассивов. В рамках этой стратегии резервы ликвидности между возвратами активов и погашением обязательств целесообразно использовать для получения дохода в коротких межбанковских кредитах (под процент r).

Так как выполнение ограничений по объёмам ликвидности актуально для моментов погашения обязательств τ, то определим агрегированный поток Y^(τ) платежей для периода Δτ между последовательными погашениями обязательств (τ – 1; τ):

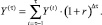(7)

Ограничение по ликвидности совокупного портфеля банка:

Y^(τ) ≥ L(t), τ ∈ [t – 1; t] (8)

является «узловым» с позиции согласованности временной структуры активов-пассивов.

В случае полной согласованности временной структуры неравенство (8) выполняется для всех t = 1, …, Т, в противном случае – только для части временных интервалов.

В модели взаимодействия портфелей активов и депозитов банка следует учитывать то обстоятельство, что кредитный портфель банка является составной частью банковского портфеля в целом: денежные потоки кредитного портфеля формируются не только за счёт средств, поступающих от ранее размещённых кредитов. По этой причине потенциальный объём средств PV(t), которыми располагает кредитный менеджер для формирования кредитного портфеля на момент времени t, может быть представлен соотношением

PV(t) = Y(τ) – L(t) + X(t); τ ∈ [t – 1; t], (9)

где X(t) – случайная величина, представляющая собой свободный остаток денежных средств банка (со знаком «+» или «–») после исполнения всех обязательств на момент времени t, которые можно направить на кредиты.

X(t) определяется из платёжного баланса банка на период t:

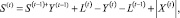(10)

где S(t) – сальдо денежного потока банка в момент времени t.

Альтернативный расчёт X(t) можно провести по остаткам денежных средств по корреспондентскому счёту банка с использованием вероятностно-статистических и эконометрических методов. Представление остатка денежных средств на корреспондентском счёте банка в виде временного ряда позволяет применять соответствующие методы анализа и моделирования [3, 8]:

– с использованием моделей авторегрессии (autoregressive – AR), скользящего среднего (moving average – MA) и смешанных моделей авторегрессии –скользящего среднего (ARMA) – для стационарных процессов и интегрированных моделей авторегрессии – скользящего среднего (ARIMA) – для нестационарных процессов;

– с использованием количественных характеристик рассматриваемого временного ряда – математического ожидания и среднеквадратического отклонения.

Анализ данных в соответствии с методологией ARIMA предполагает следующие этапы:

1. Идентификация процесса. Используются тесты, позволяющие выявить закономерности исследуемого временного ряда. В частности проводится тест на определение типа нестационарности ряда – тест Дикки– Фуллера (DF-test), и в случае необходимости исходный ряд преобразуют к стационарному виду.

2. Оценка ряда. На основе идентификации определяются характеристики модели ARMA (p, q) или ARIMA (p, d, q). Методом Бокса – Дженкинса производится оценка параметров предполагаемых моделей и определяется конечный вид наиболее приемлемой из них. На этом этапе используются информационные критерии Акаике – Шварца, а также осуществляется тест на «белый шум» остатков модели.

3. Прогноз. После проведения оценки строится прогноз исследуемого показателя путём экстраполяции по модели. В нашем случае приемлемая дальность прогноза – один модельный период. Данный подход связан с тем, что при увеличении количества прогнозных периодов растет ошибка модели, что ведёт к ухудшению качества прогноза.

Согласно подходу с использованием количественных характеристик временного ряда остатков на корреспондентском счёте банка, исходя из справедливости гипотезы о логнормальном распределении ряда 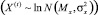, оценка X(t) осуществляется в соответствии со следующей процедурой.

В силу неотрицательности остатка на корсчёте банка будем использовать логарифмическое преобразование исходного ряда абсолютных значений Xt = (x1, x2, …, xn), t = 1, …, n (n – число наблюдений):

yt = lnxt. (11)

Тогда

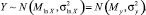
Найдём параметры распределения My и :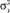

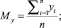(12)

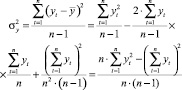(13)

(при расчете дисперсии используем несмещенную оценку).

В соответствии с ЦПТ (центральной предельной теоремой) величина 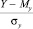распределена по нормальному закону с параметрами (0,1).

Определим минимально возможный потенциальный остаток денежных средств на корреспондентском счёте банка как нижнюю границу 99 % доверительного интервала путём обратного преобразования по формуле [3, 8]:

X(t) = exp(My – 2,33•σ_y), (14)

где 2,33 – квантиль стандартного нормального распределения, соответствующий вероятности 99 %. Поскольку минимальный уровень резервирования на возможные потери по ссудам наиболее распространенной 2-й категории качества в соответствии с требованиями регулятора составляет 1 %, выбор вероятности 99 % оправдан.

Представленные подход и численный метод дают различную оценку остатка денежных средств на корреспондентском счёте банка X(t) на следующий модельный период. Согласно подходу с использованием количественных характеристик временного ряда получим минимальный остаток денежных средств, с использованием ARIMA моделей – средний. Выбор прогнозной величины X(t) для дальнейшего расчета потенциального объёма PV(t) кредитного портфеля зависит от склонности к риску лица, принимающего решения: в случае несклонности ЛПР к риску выбирается минимальный остаток, в противном случае – средний.

Отметим, что при проведении модельных расчётов аналитик может столкнуться с рядом трудностей, связанных с низким качеством банковской статистики, в частности данных по остаткам на корреспондентском счёте банка. В нашем случае расчёт потенциального остатка денежных средств на корреспондентском счёте был проведён для выбранного коммерческого банка ХХХ. В качестве исходных данных использовался временной ряд дневных значений остатков на корреспондентском счёте банка ХХХ с 01.01.2013 по 01.01.2016 (рис. 1). Будем полагать, что модельным интервалом является месяц, таким образом, для дальнейших расчетов агрегируем исходный ряд дневных значений в месячные.

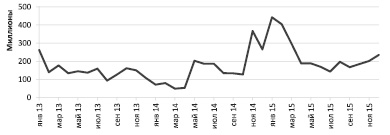
Рис. 1. Графическое представление ряда (Yt) месячных значений остатков на корреспондентском счёте банка

Очевидно, что ряд имеет непостоянные математическое ожидание и дисперсию, что объясняется нестабильностью экономической конъюнктуры в последний период (2014–2015 гг.) [6]. В данной ситуации, несмотря на плохое качество исходных данных, проведём дальнейшее эконометрическое моделирование, а адекватность результата оценим позже.

Протестируем представленный ряд на стационарность. Расчётное значение статистики Дикки – Фуллера больше критического для всех α = 0,05, т.е. можно отвергнуть гипотезу о наличии единичного корня (табл. 1).

Таблица 1

Результаты теста Дикки – Фуллера на единичный корень для ряда месячных значений Yt

Таблица 2

Результаты теста Дикки – Фуллера на единичный корень для Yt–Tt

Исходный ряд не является стационарным. Попробуем привести его к стационарному виду, исключив детерминированную составляющую. Коэффициент детерминации линейного тренда для ряда месячных значений остатков на корреспондентском счёте банка имеет низкую детерминацию (12 %), однако его исключение приводит ряд остатков к стационарному виду (табл. 2).

На пятипроцентном и десятипроцентном уровнях мы можем отвергнуть гипотезу о наличии единичного корня, а значит, на этих уровнях процесс является стационарным.

Проведём дальнейший анализ ряда Yt–Tt для определения вида модели с помощью автокорреляционной и частной автокорреляционной функции (рис. 2, 3).

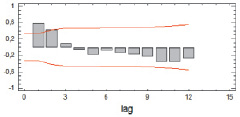
Рис. 2. График автокорреляционной функции для ряда Yt–Tt

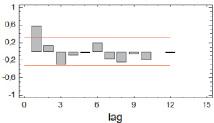
Рис. 3. График частной автокорреляционной функции для ряда Yt–Tt

Таблица 3

Исходные параметры модели AR(1)

Таблица 4

Скорректированные параметры модели AR(1)

Ряд Yt–Tt принадлежит процессу AR(1):

(yt – Tt) = α₀ + α₁•(y _t–1 – T _t–1) + ε_t. (15)

Параметры модели (15) приведены в табл. 3.

Исключим незначимую константу и оценим параметры модели (табл. 4).

Отметим, что несмотря на низкую детерминацию, модель в целом значима по критерию Фишера, следовательно, её можно использовать для прогноза.

α₁ = 0,5957 и удовлетворяет ограничению |α| < 1, что позволяет построить итоговую модель (рис. 4):

yt = Tt + 0,596•(y _t–1 – T _t–1). (16)

Проверим ошибку модели на соответствие белому шуму (рис. 5).

Прогнозное значение остатков денежных средств на корреспондентском счёте банка ХХХ составляет 226 854 531 руб.

Проведём альтернативный расчёт минимального остатка с использованием количественных характеристик рассматриваемого временного ряда – математического ожидания и среднеквадратического отклонения. Для преобразованного ряда lnyt математическое ожидание составляет 18,89, СКО – 0,49. В этом случае для 99 %-го доверительного интервала минимальный остаток денежных средств на корреспондентском счёте банка составит 51 344 104 руб.

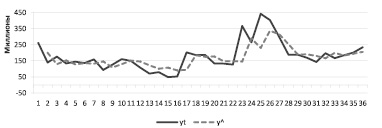
Рис. 4. Графическое представление итоговой модели и исходного ряда

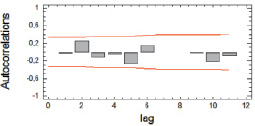
Рис. 5. График автокорреляционной функции ошибок модели AR(1) для Yt–Tt

Зная величину РV(t) (формула (9)) и долю α^(t) средств, направляемых для размещения в кредиты (выбираемую в соответствии со стратегией и кредитной политикой банка), определим величину α^(t) •РV^(t) , задающую верхнюю границу свободного остатка денежных средств для размещения в кредиты для периода времени t.

Выбор управлений по кредитному портфелю ЛПР осуществляет в зависимости от состояния ликвидности и денежных потоков Z(t) = {S(t), Y(t), L(t)}, наблюдаемых на временном интервале t.

Альтернативный алгоритм определения верхней границы свободных денежных средств банка для размещения в кредиты – с учетом нормативов ликвидности Н2, Н3, Н4 и Н5, установленных регулятором. Пусть HV(t) – величина свободных средств, рассчитанная на основе этого алгоритма.

Определим W(t) – верхний предел приращения кредитного портфеля для периода t:

W(t) = min{α^(t)•РV^(t) ; HV^(t) }. (17)

Определив фонд W(t) кредитного портфеля на момент времени t, решаем задачу формирования кредитного портфеля для периода t.

Принципиальный алгоритм решения этой задачи соответствует алгоритму выбора портфеля финансовых активов с критерием доходности и ограничениями на совокупный риск и ликвидность временной структуры. Ограничение на ликвидность требует коррекции объёма W(t) прироста кредитного портфеля с учётом необходимости резервирования части средств для покрытия дефицита ликвидности.

В случае полной согласованности временной структуры активов-пассивов на модельном интервале t (точного совпадения активов и пассивов в каждом временном промежутке τинтервала t) объём Ω^(t) свободных средств банка для размещения в кредиты в конце интервала t совпадает с определённой формулой (17) величиной W^(t) .

В случае неполной согласованности временной структуры активов-пассивов на модельном интервале t общий объём Ω^(t) планируемых кредитов не должен превосходить величины A^(t) – П^(t) , где П^(t) , A^(t) – величины соответственно пассивов и активов банка в конце модельного интервала t. В этом случае удаётся повысить согласованность срочной структуры активов-пассивов на интервале [t – 1, t] за счёт повышения ликвидности портфеля банка на промежутках ? с «разрывами» ликвидности.

Таким образом, в этом случае объём Ω^(t), направляемый на кредитование определяется выражением

Ω^(t) = min{A(t) – П(t); W(t)}. (18)

Отметим, что если П(t) – A(t) > 0 (дефицит ликвидности), кредитование возможно в исключительных случаях на величину остатка свободных средств банка за вычетом депозитов «до востребования» и приравненных к ним пассивов.

В заключение отметим, что представленная модель не является законченной: возможен учёт дополнительных ограничений на лимиты по отдельным активным операциям. Менеджеры в конкретных условиях могут дополнять и корректировать модель в соответствии с выбранной стратегией кредитования частных и корпоративных заемщиков.