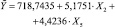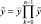Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Цель данного исследования – построение математической модели, которая учитывала бы факторы, влияющие на стоимость бывших в употреблении автомобилей в целом.

Задачи исследования:

1. Отобрать достаточные факторы для построения модели стоимости б.у. автомобилей.

2. Построить многофакторное регрессионное уравнение.

3. Оценить модель на адекватность.

4. Произвести оценку влияния факторов на стоимость б.у. автомобиля.

В процессе исследования учитывались основные параметры автомобиля, влияющие на его стоимость на вторичном рынке.

Были отобраны такие факторы, как, пробег, тип кузова, год выпуска, мощность, количество владельцев, коробка передач, тип двигателя, привод, наличие кондиционера, наличие усилителя руля, наличие зимней резины, наличие автомагнитолы, наличие стеклоподъемников, наличие сигнализации, обогрев сидений, обогрев стекол, наличие ковриков, наличие литых дисков. Была построена матрица парных коэффициентов для устранения мультиколлинеарности, если таковая имеется и проведен ее анализ Для проверки значимости коэффициентов корреляции используем t-критерий Стьюдента. Фактическое значение этого критерия определяем по формулам:

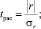
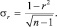(1)

Затем в несколько этапов был проведен pегрессионный анализ – заключающийся в исследовании влияния независимых переменных X1, X2, ..., Xp на зависимую переменную Y [5]. Зависимые переменные называют критериальными, а независимые переменные – регрессорами. Терминология этих переменных отражает только математическую зависимость переменных. Уравнение регрессии было применено для построения линии регрессии. Последнее позволило определить среднюю величину Y, при изменении величин Х. Итак было построено следующее регрессионное уравнение:

Y = 417564,5489817 – 0,859745052•x1 + + 20825,306•x2 + 1799,611•x3 + + 235839,626•x4, (2)

где x1 – пробег автомобиля в км; x2 – год выпуска; x3 – мощность, л.с.; x4 – количество владельцев (1 – один владелец, 0 – больше одного).

Таблица 1

Критическое значение t-статистики Стьюдента при уровне значимости 0,05 и числе степеней свободы 100: t_кр ≈ 1,984.

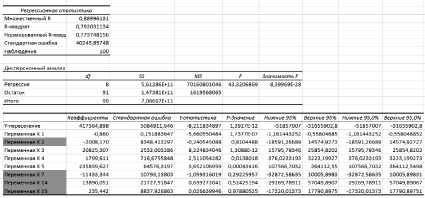
Результаты регрессионного анализа модели Y

Затем уравнение (2) было оценено при помощи математических критериев, что доказало, адекватность его построения. Оценка значимости уравнения множественной регрессии осуществлялась путем проверки гипотезы о равенстве нулю коэффициента детерминации. Коэффициент (индекс) детерминации показывает качества регрессионной модели. По-другому коэффициент детерминации дает понять, какая доля общей вариации выходной переменной Y определена зависимостью ее от входной переменной [1]. Коэффициент (индекс) детерминации был рассчитан по данным генеральной совокупности: R2 или b1 = b2 = ... = bm = 0 (гипотеза о незначимости уравнения регрессии, рассчитанного по данным основной совокупности) [2]. Для ее проверки использовался F-критерий Фишера. При этом было вычислено фактическое (наблюдаемое) значение F-критерия, через коэффициент детерминации R2, рассчитанный по данным конкретного наблюдения. По таблицам распределения Фишера – Снедоккора было найдено критическое значение F-критерия (Fкр). Для этого был задан уровень значимости α = 0,05 и два числа степеней свободы k1 = m и k2 = n – m – 1. Так как значения некоторых исходных данных больше 1 000, то можно данные либо разделить на 1 000, либо использовать решение MS Excel. Чем ближе этот параметр к единице, тем больше уравнение регрессии объясняет поведение Y [3].

Добавление в модель новых объясняющих переменных осуществилось до тех пор, пока рос скорректированный коэффициент детерминации. Так как фактическое значение оказалось F > Fkp, то коэффициент (индекс) детерминации статистически значим и уравнение регрессии статистически надежно [4]. Так же проведена проверка гипотезы об общей значимости – гипотеза об одновременном равенстве нулю всех коэффициентов регрессии при объясняющих переменных:

H0: R2 = 0; β1 = β2 = ... = βm = 0.

H1: R2 ≠ 0.

Проверка этой гипотезы осуществлялась с помощью F-статистики распределения Фишера (правосторонняя проверка). Затем был проведен статистический анализ полученного уравнения регрессии: проверка значимости уравнения и его коэффициентов, исследование относительных и абсолютных ошибок аппроксимации. Статистический анализ подтвердил правильность вычислений.

Модель (1) позволяет оценить степень влияния отдельных факторов на конечную стоимость б.у. автомобиля в числовом эквиваленте. Таким образом, пробег автомобиля в км влияет на стоимость б.у. автомобиля с отрицательным коэффициентом 0,85. Это значит, что при увеличении пробега его стоимость будет уменьшаться, но не значительно. Год выпуска также уменьшает стоимость б.у. автомобиля, при этом он имеет положительный коэффициент 20825,3, что адекватно, более ранний выпуск автомобиля снижает его стоимость с каждым годом. Коэффициент при факторе «мощность автомобиля», равный 1799,611, показывает положительную связь между ростом стоимости б.у. автомобиля и уровнем мощности автомобиля. Последний фактор «наличие одного или более владельцев» показывает, что влияние данного фактора на стоимость б.у. автомобиля велико и составляет 235839,62. Стоит учесть, что данная модель не отражает, какое именно количество владельцев и как в количественном виде влияет на стоимость б.у. автомобиля, она показывает общее влияние от наличия более одного владельца автомобиля.

Построенная в ходе исследования модель позволяет оценить и спрогнозировать стоимость б.у. автомобилей с учетом основных критериев: год выпуска, пробег, мощность и количество владельцев автомобиля, на основе реальных статистических данных, что делает модель экономически адекватным инструментом в оценки стоимости автомобиля.

Метод Брандона

Отбор и анализ факторных признаков, включаемых в модель множественной регрессии для Y.

Отбор факторных признаков проводится с помощью частных коэффициентов корреляции, необходимо, чтобы коэффициент корреляции r зависимости между результирующим показателем Y и каждым j-м фактором xj должен быть отличен от нуля, и факторы x1, x2, …, xn должны быть попарно независимыми.

На Y оказывают умеренное влияние – X1 (r _{yx1/x3,х4,х5} = 0,570255969061171), сильное влияние – X3 (r _{yx3/x1,x4,х5} = 0,801680915508622), причем связь между X1 и X4 слабая (r _{x1x4/y,х3,х5} = –0,390562532906476); связь между X1 и X5 слабая (r _{x1x5/y,х3,х4} = –0,189562532906476). Таким образом, для построения множественной регрессии выбираем пару факторов Х1Х3

• пробег, в км – X1;
• мощность, л. с. – X3.

Множественная нелинейная регрессия (Y)

Для построения уравнения множественной нелинейной регрессии был использован метод Брандона.

1. Было вычислено среднее значение:

2.

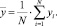
3. Каждое i-е наблюдение yi было преобразовано по формуле

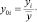
4. Для пары переменных y_0i и x_i1 так же, как и при парной регрессии, был выбран вид зависимости с максимальным уровнем спецификации по критерию Дарбина – Уотсона и по величине корреляционного отношения η:

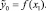
Таблица 2

Уравнения парной регрессии для YX1

Учитывая значимость коэффициентов регрессии, значимость уравнения в целом, величину корреляционного отношения и коэффициента корреляции (для линейной модели), точность аппроксимации и отсутствие автокорреляции, в качестве модели выбираем параболическую модель второго порядка:

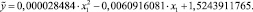
1. Вычислили значения 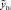и .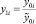

2. Для пары переменных y1i и xi3 выбрали вид зависимости с максимальным уровнем спецификации: .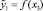

Составим аналогичную таблицу уравнения парной регрессии для YX5 (табл. 2).

Учитывая значимость коэффициентов регрессии, значимость уравнения в целом, величину корреляционного отношения и коэффициента корреляции (для линейной модели), точность аппроксимации, и отсутствие автокорреляции, в качестве модели выбираем параболическую модель третьего порядка:

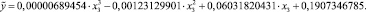
После определения 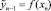строится общая формула множественной регрессии:

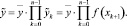
Она имеет вид

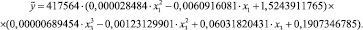
На основе проделанной работы выбрали модель с наивысшим уровнем спецификации. Спецификация моделей представлена в табл. 3:

Таблица 3

Множественные регрессии для YX1X3. Спецификации

Экономическая интерпретация уравнения регрессии

Учитывая значимость коэффициентов регрессии, значимость уравнения в целом, величину корреляционного отношения, коэффициента корреляции (для линейной модели) и автокорреляцию остатков, видно, что наиболее целесообразно выбрать параболическую зависимость. Коэффициенты нелинейной модели, построенной методом Брандона, значимы (значит, эти коэффициенты формируются под воздействием неслучайных факторов), корреляционное отношение η = 0,98543 достаточно большое (тесная связь между рассматриваемыми признаками), точность аппроксимации высокая (всего 0,43 %), автокорреляция остатков отсутствует, значит, именно эта зависимость лучше описывает исходный Y – стоимость автомобиля, (в руб.).

Уравнение нелинейной зависимости выглядит следующим образом:

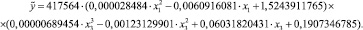
Уравнение в целом значимо, так как коэффициент детерминации очень высок R² = 0,98201, а чем больше его величина, тем больше влияние данных признаков на величину результативного. Таким образом, на повышение стоимости автомобиля будут влиять мощность и пробег (чем меньше, тем дороже).