В последние годы решение современных задач, связанных с разработкой высоконадежных регулируемых электроприводов с частотным управлением, определяется применением электрических машин переменного тока с заранее заданными свойствами. Для разработки и проектирования таких машин требуется проведение точных вычислений, позволяющих определить электромагнитные параметры [7, 5].
В системах автоматического управления повышенной точности с широким диапазоном изменения скорости вращения в настоящее время большое применение получают синхронные реактивные электродвигатели (СРД).
Следует отметить, что, несмотря на заметные успехи в исследовании синхронных реактивных электрических машин, традиционная система изучения, расчета и проектирования таких электродвигателей была построена на упрощенных цепных математических моделях. Поэтому точное построение картины магнитного поля усовершенствованных синхронных реактивных двигателей практически не представлялось возможным [4].
Так как электромеханическое преобразование энергии в любой электрической машине осуществляется через магнитное поле, то непосредственное использование его для расчета, определения параметров и интегральных характеристик СРД является наиболее перспективным и актуальным.
Целью данной статьи является представление предложенных авторами выражений, позволяющих по результатам расчета электромагнитных полей СРД получить их электромагнитные параметры.
Постановка задачи расчета магнитного поля СРД
Основные электромагнитные процессы, связанные с электромеханическим преобразованием энергии в электрических машинах, протекают в их активной зоне, поэтому первоначальные расчеты магнитного поля обычно ограничивают плоскопараллельной постановкой задачи, рассматривая лишь поперечное сечение магнитной системы машины. При этом предполагается, что геометрия расчетных областей, свойства сред и параметры, характеризующие источники поля, неизменны в направлении оси z, как показано на рис. 1. Вследствие этого описание геометрии, задание свойств, граничных условий и источников, а также обработка результатов проводится в плоскости xy, которую можно называть плоскостью геометрической модели.
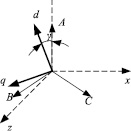
Рис. 1. Расположение координатных осей
При этом принято, что ось x направлена слева направо, а ось y – снизу вверх и эти оси неподвижны в пространстве машины. Магнитопровод ротора симметричен относительно продольной d и поперечной q осей ротора.
В этом случае вектор магнитной индукции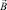 
имеет две составляющие Bx, By, а векторный магнитный потенциал 
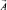, использующийся при решении таких задач, имеет единственную осевую составляющую 
.
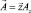Магнитное поле в поперечном сечении СРД описывается дифференциальным уравнением
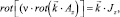(1)
где Az, Jz – аксиальные составляющие векторного магнитного потенциала (ВМП) и плотности тока; ν – удельное магнитное сопротивление (УМС); 
– орт.
В прямоугольной системе координат это уравнение преобразуется к виду
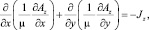(2)
где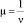 
– составляющие магнитной проницаемости по осям x, y которые задаются зависимостью B = f(H) с учетом изотропных свойств материалов при формировании модели.
Пространственное распределение тока можно описать распределением плотности этого тока. При расчете магнитных полей СРД методом конечных элементов использован прикладной программный пакет ELCUT.
При моделировании СРД в ELCUT были приняты следующие допущения:
- частота токов в обмотке статора невысока, так как статор СРД – это статор асинхронного двигателя;
- ротор СРД явнополюсный без обмотки возбуждения и постоянных магнитов, поэтому токов в роторе нет;
- магнитное поле обмотки статора и магнитное поле ротора СРД рассматриваются в координатах d и q, жестко связанных с вращающимся ротором;
- ферромагнитные материалы изотропны и кривые намагничивания этих материалов однозначны;
- источником поля является распределенный токовый слой обмотки статора и плотность тока по всему поперечному сечению обмотки одинакова.
Расчет магнитного поля проводится по поперечному сечению СРД. На внешних границах за пределами сердечника ротора и статора принимаются условия Дирихле Az = 0 [4].
Типичная картина распределения магнитного поля четырехполюсного СРД, полученная в результате расчета, представлена на рис. 2.
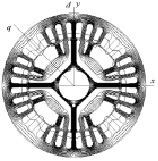
Рис. 2. Магнитное поле четырехполюсного синхронного реактивного двигателя
Вычисление электромагнитных параметров по результатам расчета магнитного поля
При анализе результатов расчета магнитного поля с помощью ELCUT можно оперировать со следующими локальными и интегральными физическими величинами:
- Локальные величины – это векторный магнитный потенциал A; вектор магнитной индукции B = rot A; вектор напряженности магнитного поля H = μ–1 B, где μ – тензор магнитной проницаемости.
- Интегральные величины – суммарная магнитостатическая сила, действующая на тела, заключенные в заданном объеме, и определяющая электромагнитный момент СРД:
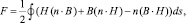
где интегрирование ведется по поверхности, окружающей заданный объем, а n – единичный вектор внешней нормали к поверхности; энергия магнитного поля в данном случае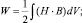 
потокосцепление на один виток обмотки в плоскопараллельном случае 
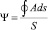, где интегрирование ведется по поперечному сечению обмотки, а S обозначает площадь этого поперечного сечения.
Для плоских задач все интегральные величины рассматриваются на 1 метр длины в осевом направлении, область расчета которых задается в плоскости модели в виде контура интегрирования.
При равномерно распределенной плотности тока потокосцепления в поперечных сечениях CРД на один усредненный виток обмотки статора определяются в виде [6]:
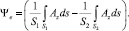(3)
Для всей обмотки статора СРД с учетом всех ее витков и активной длины полное потокосцепление можно представить следующим образом:
ψ = Wψel, (4)
где l – активная длина магнитопровода синхронного реактивного двигателя; W – число витков обмотки статора.
Для численного расчета собственной индуктивности фазы обмотки статора задаются током, протекающим в ней при отсутствии токов в остальных фазах. Тогда собственную индуктивность можно определить через векторный магнитный потенциал по выражению
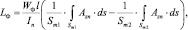(5)
где Azn – векторный магнитный потенциал поля, возбужденного током In фазы; Sm1 и Sm2 – площади поперечного сечения сторон фазы; WФ – число витков фазы.
Взаимная индуктивность между фазами может быть найдена аналогичным образом, но ток должен быть задан в одной из двух фаз, а потокосцепление можно вычислить для другой фазы.
К числу индуктивных параметров СРД, которые определяют особенности его работы и протекающие в нем процессы, относятся индуктивности La, Lb, Lc и взаимоиндуктивности Mab, Mac, Mbc фазных обмоток статора. Индуктивности и взаимоиндуктивности статорных обмоток вследствие явнополюсности ротора являются периодическими функциями угла γ между осью фазы А и продольной осью d ротора, определяющего его положение в пространстве (рис. 1).
При расчете результирующего магнитного поля СРД возможно определить также значения синхронных индуктивных параметров обмоток статора по продольной xd и поперечной xq осям. Синхронные индуктивные сопротивления СРД, как известно [3], равны
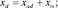
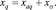(6)
где xad, xaq – сопротивления взаимоиндуктивности обмотки статора по осям d и q соответственно; xσ – сопротивление рассеяния обмотки статора.
В научно-технической литературе, например [3, 1], описано множество методов экспериментального исследования реактивных параметров электрических машин переменного тока. Наиболее часто для синхронных машин определение индуктивных сопротивлений осуществляют при питании обмоток переменным током.
Например, для определения сопротивлений xd и xq для синхронных машин наименьшее значение тока в цепи обмотки статора получают в момент совпадения оси намагничивающей силы (н. с.) статора с продольной осью ротора. Этому моменту соответствует максимальное напряжение на зажимах обмотки статора и, следовательно, индуктивное сопротивление по оси d можно определить по выражению
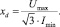(7)
При совпадении оси н. с. статора с поперечной осью ротора ток в обмотке статора имеет наибольшее значение, а напряжение на зажимах обмотки – наименьшее, и, следовательно, индуктивное сопротивление по оси q можно представить в виде
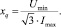(8)
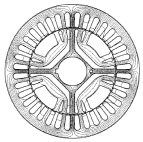
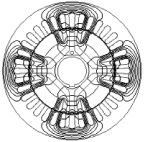
а б
Рис. 3. Картина распределения магнитного поля фазы А: а – для первой модели; б – для второй модели
Кроме того, индуктивные сопротивления рассеяния определяются для СРД методом вынутого ротора [3]. Поэтому одну из задач определения данных сопротивлений можно решить с помощью анализа картины магнитного поля СРД.
Для этого в соответствии с методикой классического эксперимента по определению синхронных индуктивных сопротивлений по продольной и поперечной осям, создаются две геометрические модели [3], картины распределения магнитного поля которых приведены на рис. 3.
Из рис. 3 следует, что в первой модели подается напряжение на фазу А, при этом ось ротора d совпадает с направлением оси намагничивающей силы этой фазы. Во второй модели ось намагничивающей силы фазы А статора совпадает с осью q ротора.
Для определения индуктивности рассеяния обмотки статора СРД без ротора была разработана модель, распределение магнитного поля в которой представлено на рис. 4. В этом случае взаимоиндукция между обмотками статора и ротора отсутствует.
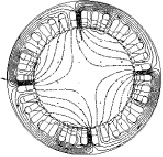
Рис. 4. Картина распределения магнитного поля фазы А без ротора
При классическом определении параметров рассеяния СРД [1] активным сопротивлением обмотки можно пренебречь, поэтому уравнение равновесия напряжения для статорной цепи можно записать в виде
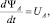(9)
где ψA – потокосцепление фазы А.
Таким образом, замерив магнитный поток, сцепленный с фазой А, в первом и во втором случаях, и используя мастер пакета ELCUT для вычисления индуктивностей, можно определить индуктивности фазы по продольной Ld и поперечной Lq осям, в соответствии с выражением L = ψ/I [8].
В этом случае индуктивные сопротивления определяются в виде
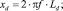
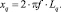(10)
Аналогично определяется индуктивность рассеяния обмотки статора xσ.
Индуктивные параметры СРД, вычисленные в результате расчета магнитных полей, приведены в таблице.
Основные результаты расчета магнитных полей
|
Ф, Вб |
I, А |
X, Ом |
|
|
Ось d |
0,6672 |
7,5 |
55,67 |
|
Ось q |
0,1309 |
7,5 |
10,95 |
|
Рассеяние |
0,003861 |
7,5 |
2, 3975 |
Зная значения xd, xq, xσ, можно определить сопротивления взаимоиндукции xad и xaq СРД по следующим выражениям:
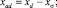
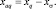
Общее потокосцепление фазы А можно определить, зная продольное и поперечное потокосцепления ψd и ψq, полученные с помощью моделей 1 и 2 [7]:
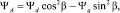(11)
где β – угол поворота ротора.
Тогда главное индуктивное сопротивление фазы А СРД определяется следующим образом:
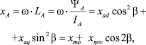(12)
где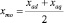 
– среднее значение индуктивного сопротивления фазы; 
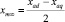– амплитуда переменной составляющей индуктивного сопротивления фазы.
Взаимные индуктивные сопротивления между фазами [2]:
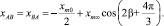(13)
Заключение
Результаты, полученные при моделировании электромагнитных полей синхронного реактивного двигателя, подтверждают возможность использования расчета полей СРД для определения их электромагнитных параметров.
Модели магнитных полей СРД, разработанные авторами, позволяют проводить расчеты электромагнитных параметров в электрических двигателях переменного тока любой конструкции.