Решения некоторых задач определения выносливости оболочек и пластин приведены в работах [1, 2, 3], где рассмотрены статистически определимые элементы конструкций. В данной работе приведена методика решения аналогичных задач для статически неопределимых элементов конструкций. Подобная методика описана в [4], где рассмотрен случай действия на элемент конструкции кратковременной статической нагрузки.
Для определения предельного равновесия статически неопределимых конструкций часто используют так называемые кинематический и статический методы теории предельного равновесия, которые базируются на соответствующих теоремах, в общем виде сформулированных и доказанных А.А. Гвоздевым [5]. При этом применяют понятия о виртуальных полях перемещений и напряжений. Классическая теория предельного равновесия разработана для тех случаев, когда полностью в пластическое состояние одновременно переходят столько сечений конструкции, что она в итоге превращается в механизм хотя бы с одной степенью свободы. Для упрощения расчётной модели часто используют диаграмму деформирования «жёсткопластического» тела [6].
При разрушении от многоцикловой нагрузки не наблюдаются, как правило, заметные пластические деформации. Это разрушение внешне выглядит как хрупкое. Однако микропластические деформации имеют при этом место, о чём свидетельствует, в частности, повышение температуры испытуемых на многоцикловое нагружение образцов.
Чтобы обосновать использование теории предельного равновесия на случай многоциклового нагружения, нами было введено понятие о виртуальных диаграммах деформирования [3]. При многоцикловом нагружении процесс разрушения материала конструкций начинается задолго до потери ими несущей способности. В результате действия нагрузок идёт процесс накопления повреждений. В момент, непосредственно предшествующий потере несущей способности конструкции, материал в зоне разрушения приобретает совсем другие свойства, чем они были до приложения нагрузок.
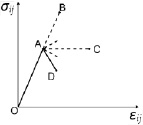
Рис. 1. Диаграммы связи между напряжениями σij и деформациями εij
На рис. 1 изображена условная диаграмма связи между напряжениями σij и деформациями εij (i, j = 1, 2, z). Участок ОА соответствует устойчивому состоянию, а участок AD – неустойчивому состоянию материала. Допустим, что переход от устойчивого состояния в неустойчивое происходит непрерывным образом, за время Δt. Тогда материал за этот промежуток времени испытывает целый спектр состояний, виртуальные диаграммы σij – εij, соответствующие этим состояниям, располагаются в пределах угла BAD (рис. 1, штриховые линии).
Виртуальной диаграммой σij–εij будем называть такую, которая имела бы место, если бы удалось стабилизировать свойства материала, которые он имеет в рассматриваемый момент времени внутри промежутка Δt. Среди виртуальных диаграмм есть и такая, которая параллельна оси σij (линия AC на рис. 1). Состояние материала, соответствующее виртуальной диаграмме AC, примем за предельное. Если в предельном состоянии упругие деформации малы, и ими можно пренебречь, то в итоге приходим к жёсткопластической модели деформируемого твёрдого тела.
Полагаем, что до мгновения катастрофического разрушения конструкции напряжения в ней претерпевают целое число циклов. Допустим, что предельная поверхность прочности в пространстве амплитудных значений напряжений σij,a может быть описана следующим уравнением:
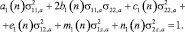(1)
Здесь n – число циклов до разрушения; коэффициенты a1(n), …, n1(n) подлежат экспериментальному определению. Правая система декартовых координат связана с поверхностью приведения S0 оболочки или пластины, ось z ортогональна поверхности S0, оси α1 и α2 являются касательными к соответствующим линиям главных кривизне оболочки. При записи (1) принято допущение, что σ zz,a ≈ 0.
Используя ассоциированный с (1) закон деформирования [6], гипотезы кинематического характера и следуя работе [1], можно получить следующие параметрические уравнения предельной поверхности прочности в пространстве амплитудных значений внутренних сил и моментов:
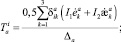
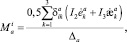
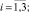(2)
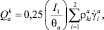
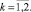
Здесь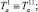 
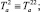
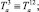
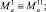
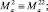
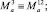
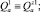
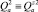– обобщённые силы;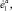 
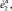
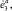
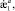
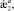
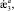
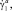
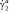– соответствующие обобщённые перемещения; 
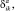Δa, θa – определители, элементами которых являются коэффициенты уравнения (1); интегралы Ij определяются формулой
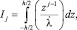
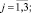(3)
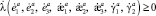– скалярная функция; h – толщина оболочки или пластины.
Предлагаемая нами методика решения рассматриваемых здесь задач ориентирована на использование численных методов и ЭВМ. Дискретизация объекта расчёта осуществляется с использованием абсолютно жёстких конечных элементов, каждый из которых в трёхмерном пространстве имеет шесть степеней свободы (опорные абсолютно жёсткие конечные элементы неподвижны, или их перемещения заданы). Диссипация энергии деформации учитывается только вдоль обобщённых шарниров разрушения, расположенных между соседними абсолютно жёсткими конечными элементами. Используется вариант кинематического метода теории предельного равновесия, который формально совпадает с тем, что описано в работе [4]. Аппроксимируя предельную поверхность (2) вписанным многогранником и используя принцип максимума Мизеса [6], задачу сводим к задаче линейного программирования, решение которой позволяет определить min μ+ , где μ+ – монотонно возрастающий кинематически возможный параметр внешней нагрузки.
Уравнение баланса мощностей имеет следующий вид [6]:
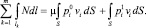(4)
Здесь lk – длина k-й линии разрушения; m – число линий разрушения; S – площадь поверхности приведения сил; N – мощность внутренних обобщенных сил, приходящаяся на единицу длины линии разрушения; vi – компоненты вектора скорости движения точки оболочки, где приложена сила pi; μ – параметр, пропорционально которому растут внешние нагрузки. По повторяющемуся индексу i(i = 1, 2, 3) производится суммирование.
Предельную поверхность аппроксимируем выпуклым многогранником, i-я вершина которого определяется вектором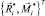 
, 
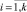, k – число вершин аппроксимирующего многогранника. Здесь Ri, Mi – погонные силы и моменты, приложенные к сечению поверхности S0.
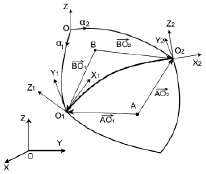
Рис. 2. Схема расположения линии разрушения O1O2 на границе абсолютно жёстких конечных элементов
На рис. 2 линия O1O2 является обобщённым шарниром разрушения между двумя абсолютно жёсткими конечными элементами. Точка A является полюсом одного конечного элемента, точка B – другого. На мощности погонных внутренних сил и моментов на концах линий разрушения O1O2 (рис. 2), развиваемые ими на разрывах скоростей соответствующих перемещений и поворотов, согласно постулату Друккера [6], можно наложить следующие ограничения [7]:
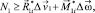
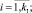
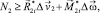
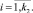(5)
Здесь k1, k2 – количество вершин предельных многогранников, соответствующих точкам О1 и О2 соответственно.
Вдоль линий разрушения используем линейную аппроксимацию функции N. В итоге получаем следующую задачу линейного программирования: найти min m+, где
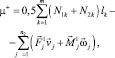(6)
при условии
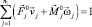(7)
и при соблюдении ограничений вида (5). Здесь j – номер жесткого элемента; n1 – число жестких элементов, на которые действуют нагрузки, зависящие от параметра m; n2 – число жестких элементов, на которые действуют нагрузки, не зависящие от параметра m. Здесь внешние силы, действующие в пределах отдельного жесткого диска, приведены к его полюсу. Результатом этого являются сосредоточенные силы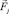 
и сосредоточенные моменты 
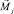, приложенные к соответствующим полюсам.
В качестве примера рассмотрим расчёт прямоугольной стальной плиты, жёстко заделанной по контуру, на которую действуют две сосредоточенные вертикальные силы в точках A и B, изменяющиеся по гармоническому закону синхронно и синфазно (рис. 3). Размеры плиты 6×3×0,01 (м). Предел выносливости для материала плиты принят σ–1 = σT/2 = 120 МПа. Уравнение (1) для рассматриваемого случая имеет вид
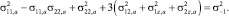(8)
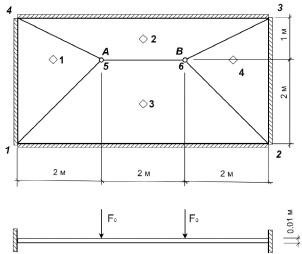
Рис. 3. Схема абсолютно жёстких конечных элементов и многоцикловой нагрузки для прямоугольной стальной плиты
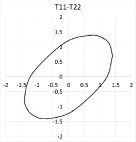
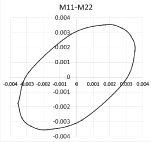
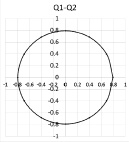
а б в
Рис. 4. Сечения предельной гиперповерхности плоскостями а – Т11–Т22 (МН/м); б – М11–М22 (МН·м/м); в – Q1–Q2 (МН/м)
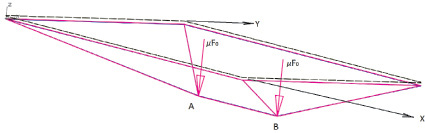
Рис. 5. Схема разрушения плиты, смоделированная по вычисленным скоростям перемещений абсолютно жёстких конечных элементов
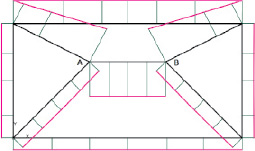
Рис. 6. Эпюры скоростей диссипации
Скорости перемещений полюсов абсолютно жёстких конечных элементов и поворотов вокруг полюсов
|
Номер диска |
vX |
vY |
vZ |
ωX |
ωY |
ωZ |
|
1 |
0,000628114 |
0,000382195 |
–0,249864047 |
0 |
0,248752446 |
0 |
|
2 |
0,002215713 |
–0,001171394 |
–0,249449905 |
0,494492644 |
–5,91971E–08 |
2,46157E–05 |
|
3 |
–0,000312883 |
0,000626765 |
–0,250554607 |
–0,249445393 |
0 |
0 |
|
4 |
7,76925E–05 |
–0,000613673 |
–0,249744786 |
–0,000245912 |
–0,248869753 |
2,42546E–05 |
Здесь напряжения в МПа, нагрузки – в МН.
На рис. 4 приведены некоторые сечения предельной поверхности, построенные с использованием уравнений (4), (2).
На рис. 5 приведена схема разрушения рассматриваемой плиты, определённая из условия достижения min μ+ ; на рис. 6 приведена соответствующая эпюра скоростей диссипации энергии деформации N. В таблице приведены скорости перемещений полюсов абсолютно жёстких конечных элементов, указанных на рис. 3 ромбиками, и повороты жёстких элементов вокруг этих полюсов. Соответствующее значение min μ+ = 0,04. Здесь XYZ – глобальная система координат, неподвижно связанная с пластиной до деформации.
В заключение отметим, что полный переход в пространства виртуальных величин позволил нам использовать теорию предельного равновесия для определения предельной несущей способности конструкций в случае их многоциклового нагружения. Изложенная выше методика позволяет определять минимальную верхнюю оценку амплитуды разрушающей нагрузки Fразр = min μ+·F0.