Инвариантные системы представляют собой новый класс систем управления, имеющих высокие показатели качества и точности управления. В инвариантной системе влияние внешних возмущающих воздействий в процессе регулировки должно быть сведено к минимуму.
В работе [4] рассматриваются инвариантные системы модального управления с идентификатором на базе следящей системы при наличии возмущающих воздействий. Под возмущениями, нарушающими состояние равновесия, понимается влияние воздействий, выводящих систему из заданного положения.
Целью данной статьи является синтез инвариантной системы адаптивного модального управления с идентификатором на базе следящей системы, которая имеет несколько входов, в том числе с управляющим входом и входами возмущающих воздействий.
Следящие системы находят широкое применение в различных отраслях техники. Они используются при автоматизации производственных процессов и в вычислительной технике.
В простейшем случае рассмотрим для стандартной MISO-системы варианты подхода с двумя входами к проблеме обеспечения инвариантности (рис. 1), на рис. 2 показана структурная схема системы с компенсацией Wk.
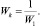(1)
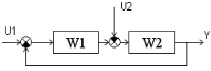
Рис. 1. Схема стандартной MISO-системы, где U1 - вход системы; U2 - вход возмущающего воздействия
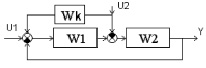
Рис. 2. Структурная схема системы с компенсацией, где U1 - вход системы; U2 - вход возмущающего воздействия
В случае, когда неизвестны параметры объекта, но получена дискретная модель идентификации системы в пространстве состояний, передаточная функция имеет вид
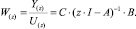(2)
Получено Y(z) = W11U1 – W21U2, где W11, W21 – передаточные функции по первому и второму входам.
В общем виде передаточные функции замкнутой системы относительно первого и второго входа имеют вид
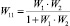и 
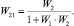(3)
Соответственно, если известны передаточные функции W11 и W21, путем деления W11 на W21, получим неизвестную передаточную функцию W1.
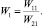(4)
После компенсации возмущения могут быть использованы любые методы модального управления, чтобы рассчитать параметры модального регулятора. Для получения векторов обратных связей P согласно уравнению
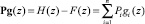(5)
была построена система уравнений, при решении которой были найдены векторы обратных связей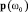 
, согласно методике, изложенной в [2].
Общую структуру синтеза инвариантной системы модального управления при неизвестных параметры объекта можно свести к следующим этапам:
– Проведение структурной и параметрической идентификации объекта. Получение модели идентификации в пространстве состояний.
– Синтез компенсации в соответствии с формулами (1), (4).
– Синтез модального регулятора по методике, изложенной в [2].
– Моделирование полученного регулятора и объекта.
Для идентификации использовался System Identification Toolbox в среде MATLAB [3]. Для проверки метода рассмотрим следящую систему, которую реализуем в среде MATLAB/Simulink.
При синтезе инвариантной системы адаптивного модального управления для следящих систем задача может быть решена с помощью следующих этапов:
– Моделирование основных объектов в среде MATLAB/Simulink.
– Построение объектов с изменяющимися параметрами в среде MATLAB/Simulink.
– Построение блока «Компенсации» в среде MATLAB/Simulink.
– Построение блока «Возмущающее воздействие» в среде MATLAB/Simulink.
– Построение блока «Адаптивный модальный регулятор» в среде MATLAB/Simulink.
– Моделирование полученной системы управления.
В соответствии с принципиальной схемой исследования проводились на структурной схеме следящей системы (рис. 3), смоделированной в MATLAB.
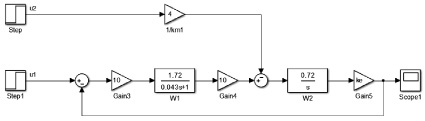
Рис. 3. Смоделированная структурная схема следящей системы
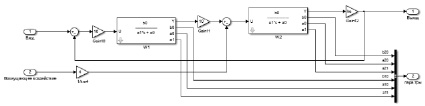
Рис. 4. Блок следящей системы с изменяющимися параметрами
Для проверки работоспособности разработанного адаптивного регулятора в этом приложении проектируется блок следящей системы с изменяющимися параметрами в среде Matlab/Simulink. Изменения параметров W1 и W2 и схема блока следящей системы представлены на рис. 4.
При этом блоки W1, W2 являются masked block, вновь созданным в среде Simulink. Отметим, что W1 и W2 являются передаточными функциями первого порядка и процедура построения этих блоков указана в [1].
Для нашей системы требуется только передаточная функция первого порядка. Однако будут небольшие изменения в самонастройке моделирующих коэффициентов.
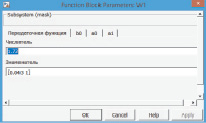
Рис. 5. Моделирующие коэффициенты для передаточной функции W1
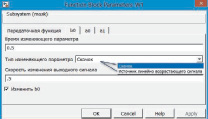
Рис. 6. Самонастройка для передаточной функции W1 – коэффициент b0
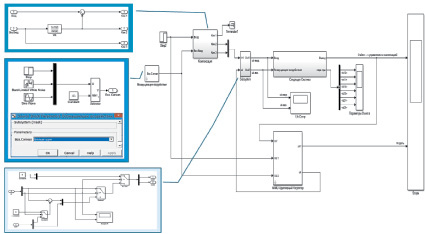
Рис. 7. Схема инвариантной адаптивной модальной системы
В этом блоке самонастройки передаточной функции параметрами для ввода являются числитель и знаменатель передаточной функции. При этом ввод проводится только для передаточной функции первого порядка.
Далее вводятся параметры b0, a0 и a1. На рис. 6 можем выбирать:
– Время начала изменения параметров.
– Способ изменения параметров: скачком или источником линейно возрастающего сигнала.
– Скорость изменения выходного сигнала (slope): это зависит от выбора способа изменения параметров.
– Последним является самонастраивание с разрешением или нет изменения этого параметра в процессе моделирования. При желании его изменения можно оперировать со знаком произведения, и наоборот.
Самонастройка для коэффициентов a0 и a1 проводится аналогичным образом, как для b0.
После построения блока следящей системы с изменяющимися параметрами проводится сопряжение с созданным в предыдущих этапах регулятором. В результате получена схема инвариантной адаптивной модальной системы (рис. 7).
Здесь:
– Блок «Возмущающее воздействие» позволяет выбирать тип помехового сигнала. Этот блок позволяет выбирать один из трех типов помехового сигнала: скачок, белый шум или синусоидальный (Sin).
– Блок «Компенсация»: формирует сигнал компенсации помех для подачи на объект управления. Этот блок получает параметры из блока «Адаптивный модальный регулятор» для создания параметра компенсации системы.
– Блок «Subsystem»: предназначен для коммутации режима идентификации объекта управления или режима управления в процессе моделирования системы.
– Блок «Адаптивный модальный регулятор»: осуществляет идентификацию объекта управления, расчет параметров компенсации и регулятора, обнаруживает изменения параметров объекта управления и вводит новые параметры объекта управления, набора параметров компенсации и регулятора. Этот блок построен по программам m-code в среде Matlab/Simulink. Его задачи: идентифицирует начальный объект управления в любой момент времени при наличии изменения параметров объекта управления; расчет параметров компенсации по методике в [4]; вычисляет параметры регулятора по алгоритмам модального управления в [2]; обнаруживает изменение параметров объекта управления; формирует импульс идентификации для объекта управления в виде импульса PRBS (псевдослучайного двоичного сигнала).
Алгоритм управления системы показан на рис. 8.
Рис. 8. Процесс управления системы, где e – ошибка рассогласования между выходами объекта управления и модели [5]
.
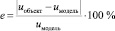Полученные результаты моделирования системы при T = 0,001s, q1 = 1, w0 = 35. При этом помеховые сигналы соответствуют одному из трех типов: белый шум, сигнал со скачком и синусоидальный (Sin).
Параметры объекта управления изменяются скачком при Db0/b0 = 0,5, Da0/a0 = 0,5, Da1/a1 = 0,1 (рис. 9).
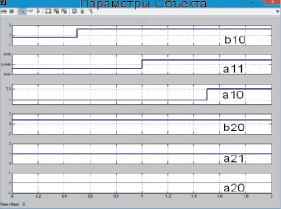
Рис. 9. Параметры объекта управления, изменяющиеся скачками
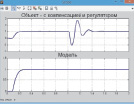
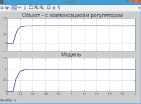
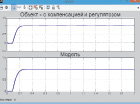
а б в
Рис. 10. График переходного процесса в системе при подаче на вход возмущающего воздействия любых сигналов: а – белый шум; б – скачок; в – синусоида
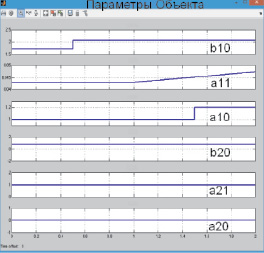
Рис. 11. Параметры объекта управления по скачкам и по закону ramp
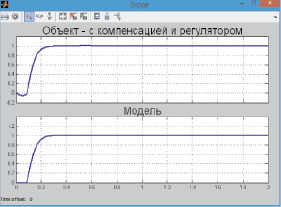
Рис. 12. График переходного процесса – возмущающего воздействия – Белый шум
Соответствующие выходные сигналы системы и модели получены на рис. 10.
Для помехового сигнала в виде сигнала со скачком и сигнала синусоидального (Sin) получены аналогичные результаты.
Параметры объекта управления изменяются скачком при Db0/b0 = 0,2, Da0/a0 = 0,2, а коэффициент a1 изменяется по закону ramp со значением Da1/a1 = 0,1 (рис. 11), а полученный результат на рис. 12.
Выводы
При моделировании системы по разным значениям параметров T, q1 и w0 для разных типов помехового сигнала получены следующие результаты:
– Система управления остается асимптотически устойчивой с небольшим изменением значений коэффициентов b10, a10, b20, a20. При большом изменении (до 50 %) значений начальных коэффициентов система остается управляемой с небольшим перерегулированием. Система управления остается асимптотически устойчивой при медленном изменении параметров объекта управления.
– Изменение параметров a11 и a21 влияет наиболее существенно на качество управления системы. При изменении скачком в 1,5 раза значений коэффициентов a11 или a21 система управления выдает достаточно большое перерегулирование для помехи типа белый шум. Однако системе удается восстановить устойчивое состояние. Помеховый сигнал в виде белого шума на входе U2 влияет больше всего на систему управления. Для устранения этого недостатка можно заменить алгоритм идентификации многомерного объекта управления в замкнутой системе рекуррентным алгоритмом.
– Система управления является устойчивой для помеховых сигналов в виде сигнала со скачком и синусоидального (Sin).