При взаимодействии композитов с агрессивными средами могут наблюдаться несколько типичных кинетических режимов (рис. 1), связанных с одновременным проявлением набухания и растворения [2, 4, 5, 11, 15]. Проницаемость для агрессивных сред дисперсно-наполненных композитных материалов, сопровождающаяся набуханием и растворением, является одним из важнейших эксплуатационных показателей [1]. Механизм набухания не поддается всестороннему анализу с позиции простых соображений. В общем случае он включает адсорбацию молекул среды на поверхности композита, диффузию среды в объем материала, физико-химические воздействия среды с матрицей и наполнителем, отвод продукции реакции от поверхности взаимодействия, образование из продуктов реакции слоя, препятствующего конвективному транспорту среды в объем композита [1, 6–9, 13, 14, 16–19, 21, 22].
К первому из кинетических режимов (рис. 1, а) относится режим монотонного приближения параметра к стационарному значению gm, связанному с ограниченным набуханием композитного материала, при котором преимущественно осуществляется физическое взаимодействие среды с материалом.
В начальный период ограниченного набухания среда интенсивно проникает в композит через поверхностные трещины, поры и другие дефекты. В этом случае количество массы g, продиффундировавшей в композит среды, асимптотически стабилизируется на некотором значении gm. С течением времени величина gm остается неизменной. Рассматриваемый кинетический режим в общем случае описывается следующим уравнением:
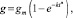 (1)
(1)
где п – постоянный эмпирический коэффициент.
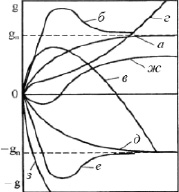
Рис. 1. Кинетические режимы взаимодействия композитных материалов с агрессивными средами (пояснения в тексте)
Для характерной кинетической кривой, проиллюстрированной на рис. 2, а, эмпирический коэффициент имеет значения n > 1, тогда как для кривой, изображенной на рис. 2, б, – n < 1.
Данные экспериментов часто приводят к зависимостям типа «прямой овершут» (рис. 1, б) с кинетикой, отображаемой зависимостью
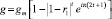 , (2)
, (2)
где 2 > r1 > 1 – параметр роста процесса.
Здесь механизм процесса непосредственно определяется последовательностью проявления эффектов набухания и растворения. В начальный период экспозиции композита в среде за малый промежуток времени прирост массы g, обусловленный диффузионным проникновением среды в материал, резко увеличивается и превышает асимптотический предел gm. Затем происходит последовательное снижение ее величины до стационарного значения gm. Отличительной особенностью таких процессов является то обстоятельство, что приближение к асимптоте gm осуществляется «сверху», в результате понижения параметра g (рис. 3).
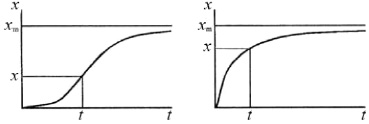
а б
Рис. 2. Типичные кинетические закономерности изменения физико-механических характеристик
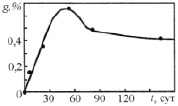
Рис. 3. Режим набухания «прямой овершут» эпоксидного композита (отвердитель 3-диметиламинопропанол) в 30 % растворе едкого натра [12]
Снижение g в процессе набухания определяется ограниченной деструкцией и вымыванием дефектных поверхностных слоев материала, что обусловлено физико-химическим взаимодействием со средой. Подобный режим с высоким параметром роста – r1 > 1 свидетельствует о малой пригодности материалов и конструкций на их основе для эксплуатации в подобных условиях.
Набухание с растворением («неограниченное набухание») определяется последовательностью процессов ограниченного набухания и неограниченного растворения (рис. 1, в и 4). Режим считается неприемлемым для технических материалов.
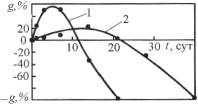
Рис. 4. Режим неограниченного набухания эпоксидного композита (отвердитель ПО-ЗОО) в концентрированных кислотах [20]: 1 – серная; 2 – азотная
Разгонное набухание (рис. 1, г и 5) наблюдается в том случае, когда диффузия среды в объеме композитного материала доминирует и не ограничена, а процессы растворения и деструкций активизируются с запозданием.
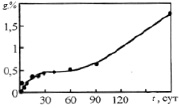
Рис. 5. Режим разгонного набухания эпоксидного композита (отвердитель ПЭПА) в 20 % растворе едкого натра [20]
Кинетика массопоглощения при разгонном набухании композитного материала выражается уравнением (2) при r1 > 2, а сам режим не соответствует условиям длительной эксплуатации композитного материала.
Режим ограниченного растворения (рис. 1, б и 6, а) противоположен режиму ограниченного набухания (см. рис. 1, а) и описывается зависимостью
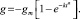 (3)
(3)
При поверхностном растворении, когда величина стационарного значения – gm незначительна, режим может быть принят за рабочий.
Режим разгонного растворения (рис. 1, ж и 6, б) характеризует композитный материал как абсолютно нестойкий в условиях действия среды.
Проявление режима «обратный овершут» (рис. 1, е и 7, а) связано с быстрым поверхностным растворением и последующим ограниченным набуханием. При этом первый процесс преобладает над вторым и поэтому параметр g остается в области отрицательных значений. Такой режим определяется кинетикой
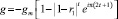 (4)
(4)
и также может быть использован в качестве рабочего.
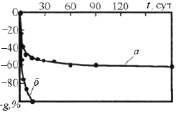
Рис. 6. Режимы ограниченного растворения (отвердитель ПЭПА) (а) и разгонного растворения (отвердитель 3-диметиламинопропанол) (б) эпоксидного композита в концентрированной серной кислоте [12]
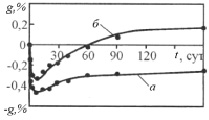
Рис. 7. Режимы «обратный овершут» (а) и «ложный старт» (б) для эпоксидного композита (отвердитель АФ-2) [20]. Композиты экспонировались в воде (а) и в концентрированной соляной кислоте (б)
Наиболее предпочтителен в условиях эксплуатации режим «ложного старта» (рис. 1, з и 7, б), который является результатом сращивания асимптотик растворения и набухания, протекающих одновременно. Здесь подрастворение наружных дефектных слоев способствует кальматированию поверхностных пор и микротрещин продуктами деструкций, тем самым создавая барьер для дальнейшего диффузионного проникновения среды в массив материала. В результате эффективное набухание может значительно снижаться в сравнении с монотонной кинетикой (см. рис. 1, а).
Рассмотрим кинетические зависимости, которые имеют вид кривых (рис. 8, с). В этом случае параметр х в начале процесса принимает отрицательные значения, но в дальнейшем монотонно увеличивается. Процесс вновь проходит через стартовое значение параметра х = 0 (при t = t2), после чего следует приближение к аттрактору xm. В данной ситуации реализуется сценарий «ложного старта», когда начало роста параметра х > 0 смещается по временной оси в точку t = t2, х = 0 (рис. 8, с).
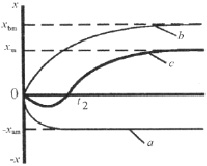
Рис. 8. Кинетические зависимости режима «ложный старт»
Подобный эффект имеет непротиворечивую интерпретацию при использовании модели сращивания асимптотик [15].
Пусть в системе одновременно наблюдается протекание двух конкурирующих процессов, один из которых дает асимптотику (рис. 8, а) в области отрицательных значений параметра х:
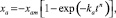 (5)
(5)
другой связан с монотонным изменением х в области положительных величин (рис. 8, в):
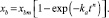 (6)
(6)
Очевидно, что эффективный процесс описывается зависимостью [1]:
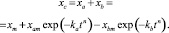 (7)
(7)
Если в начале процесса
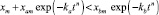 ,
,
что определяется условием ka >> kb, то эффективная кинетика будет развиваться по сценарию «ложного старта» (рис. 8, с). В данном аспекте интерес представляет время t2 «ложного старта». Поскольку ka >> kb, процесс xa = f(t) с соответствующей зависимостью (7) протекает гораздо интенсивнее и быстро заканчивается, когда exp(–katn) > 0. «Ложный старт» определяется условием хс = 0. С учетом этого (6) принимает вид
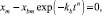
откуда окончательно получим
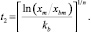 (8)
(8)
Когда параметр роста начинает превышать величину rt = 2, происходит бифуркационная смена кинетических режимов, схематически изображенная на рис. 9. В результате режим сходимости к аттрактору хт сменяется на режимы сходимости к бесконечности.
Произведем анализ возможных кинетических режимов для условия (r > 2) расходимости решений параметрического равенства:
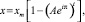 (9)
(9)
где 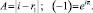
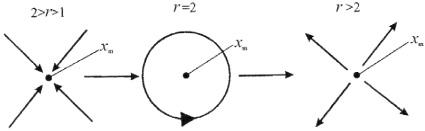
а б в
Рис. 9. Схематическое изображение бифуркационной смены кинетических режимов [12]: а – сходимость решений; б – предельный цикл; в – расходимость решений
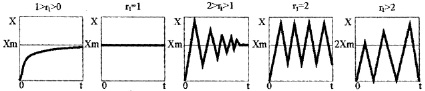
а б в г д
Рис. 10. Зависимости, соответствующие решению уравнения 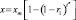 [3]
[3]
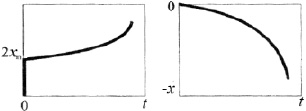
а б
Рис. 11. Стробоскопические отображения эволюционной кривой
Поскольку в практике преимущественно реализуются процессы с плавным изменением изучаемого параметра х, рассмотрим лишь стробоскопические отображения эволюционной зависимости (рис. 10, б), которые описываются параметрическими выражениями
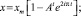 (10)
(10)
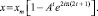 (11)
(11)
В подобном рассмотрении выделяются два стробоскопических отображения в виде верхней (с нечетными временными интервалами) и нижней (с четными временными интервалами) огибающими [8], характерный вид которых изображен на рис. 11.
Следует отметить, что оба типа зависимостей характеризуют поведение неустойчивых (разгонных) процессов с аттрактором в бесконечности. Так, кривая рис. 11, б отражает процесс активного растворения композита в агрессивной среде, вплоть до полного перехода матричного материала в раствор, когда относительное изменение массы образца непрерывно снижается. Такой процесс, протекающий в режиме стробоскопического отображения с четными временными интервалами (рис. 10, б), является типично разгонным с аттрактором в бесконечности. Для данного примера аттракторным проявлением служит полная деструкция материала композита в результате растворения матричного связующего. Аналитическое описание кинетики растворения дается уравнением (10) с модулем А > 1.
Отдельного рассмотрения заслуживает стробоскопическое отображение с нечетными временными интервалами (рис. 10, б и 11, а), типичное для неограниченной ползучести, протекающей в разгонном режиме. Аттракторное проявление при неограниченной ползучести реализуется в виде разрушения. Здесь параметр х представляется деформацией ползучести е. В этой связи согласно (11) эволюция ползучести описывается зависимостью
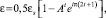 (12)
(12)
где εs – сумма мгновенной упругой деформации и деформации неустановившейся стадии ползучести; А > 1 – модуль параметра (1 – r1) при r1 > 2. Поскольку излагаемые результаты относятся к изучению кинетических процессов с особенностями, ограничимся лишь записью уравнения (12).
В отличие от режима «ложного старта» с первичным ограниченным растворением и последующим ограниченным набуханием, существуют процессы, когда изначально доминирующим является ограниченное набухание, переходящее в разгонное неограниченное растворение. Подобным образом протекает процесс набухания полимерных композитов в особо агрессивных средах, способных растворять полимерную матрицу.
Вначале, в результате осмотического процесса диффузии среды в массив композита происходит набухание матричного материала, что сопровождается ростом массопоглощения (рис. 12, а). По мере набухания постепенно развивается процесс растворения полимера, который при длительной экспозиции композитного материала в агрессивной среде становится доминирующим (рис. 12, b). При этом масса композита неуклонно понижается. Примечательно, что итоговая стадия процесса является разгонной и заканчивается полной деструкцией материала.
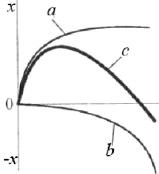
Рис. 12. Кинетика набухания с переходом в растворение
В соответствии с выражениями
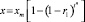
и
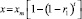 (13)
(13)
кинетика процесса набухания с последующим растворением (рис. 12 с) представляется в виде аддитивного эффекта [6]:
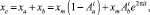 (14)
(14)
где Aa = (1 – ra) < 1; ra < 1 – параметр роста ограниченного набухания; Ab = |1 – rb| > 1, rb > 2 – параметр роста неограниченного растворения.
Проведенное обсуждение линейной модели эволюционных процессов прежде всего обусловлено возможностью рассмотрения тех режимов динамических систем, которые невозможно интерпретировать классическим представлением:
x = xm(1 – e–kt). (15)
Особенности, связанные с проявлением стробоскопических отображений, чаще рассматриваются не с позиции единой кинетической модели, а как отдельные эффекты либо наслоения процессов, что в целом затрудняет понимание механизма кинетических трансформаций. В этой связи параметр роста r1 является независимым показателем в оценке сложного поведения систем. Ограниченность уравнения (14) непосредственно связана с узким диапазоном (1 > r1 > 0) изменения величины управляющего параметра r1. В свою очередь предложенные параметрические кинетические уравнения (13), включающие параметр роста r1 как динамическую характеристику, позволяют расширить применимость теоретических решений для класса процессов, у которых r1 > 1, что существенно повышает эффективность кинетических прогнозов в оценке стационарных показателей структуры и свойств материалов и конструкций.
Таким образом, в результате проведенных исследований кинетических режимов набухания и растворения композитов в агрессивных средах представлен общий механизм набухания композитных материалов, рассмотрены различные режимы их взаимодействия с агрессивными средами. Описаны типичные кинетические процессы, протекающие при эксплуатации композитных материалов. Представлены графические зависимости, подробно описанные методами математического моделирования с получением функциональных зависимостей, с высокой точностью описывающих изменение исследуемых параметров. Выявлены экстремальные значения функций кинетических режимов в зависимости от исследуемого материала и действия среды от времени.



