Помехи, обусловленные рассеянием излученной энергии на неоднородностях электронной концентрации области E ионосферы (авроральных неоднородностях (АН) северных широт и магнитно-ориентированных неоднородностях (МОН) Е-слоя среднеширотной ионосферы), оказывают существенное влияние на качество функционирования РЛС дальнего обнаружения (РЛС ДО) диапазона УКВ. Наличие помех приводит к перегрузке системы первичной обработки сигналов, формированию ложных траекторий и снижению удельной доли энергии, идущей на обслуживание реальных объектов.
В статье представлен подход к моделированию функционирования РЛС ДО при воздействии естественных пассивных помех, обусловленных влиянием ионосферы.
Наблюдаемые РЛС ДО АН северных широт и МОН Е-слоя среднеширотной ионосферы, как правило, находятся в диапазоне высот 95–125 км, при этом толщина слоя неоднородностей составляет 0,5–20 км, а их продольный и поперечный размеры могут иметь величину до нескольких сотен километров [8, 10].
Результаты экспериментальных исследований авроральных помех и радиоотражений от МОН Е-слоя среднеширотной ионосферы показали, что даже в сравнительно небольших рассеивающих объемах (не более одного кубического километра) содержится ансамбль «псевдонезависимых» отражателей, движущихся относительно друг друга [2]. Соответственно, амплитуда результирующего отраженного сигнала является суперпозицией большого набора составляющих, соответствующих элементарным волнам со своими рассеивающими центрами (случайными амплитудами и фазами).
Все неоднородности ионосферы, расположенные в пределах общего объема и облучаемые передающей антенной, становятся источниками рассеянного излучения, которое воздействует на приемную антенну. Мощность сигнала на входе приемной антенны, создаваемая объемом рассеяния, определяется формулой [2]:
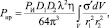(1)
где PИ – излучаемая мощность, Вт; D1 и D2 – коэффициенты направленности передающей и приемной антенн; λ – длина волны, м; η – коэффициент потерь из-за среды распространения, неидеальности трактов обработки сигналов и др., 0 ≤ η ≤ 1; r1 и r2 – расстояния от передатчика и приемника до центра элемента dV рассеивающей области, км; σ′ – удельная ЭПР, представляет собой отношение полной наблюдаемой ЭПР к величине импульсного объема, освещаемого РЛС (размерность м2/м3 = 1/м).
При расчетах обычно пользуются не мощностью принятого сигнала, а ее отношением к мощности шумов Pш на входе РЛС – отношением сигнал/шум (ОСШ) q = Pпр/Pш.
Объединяя все параметры, относящиеся к РЛС, в один множитель, который называют потенциалом РЛС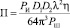 
, учитывая, что для РЛС ДО r1 ≈ r2, получим
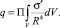
На практике потенциал РЛС определяется по результатам натурных экспериментов путем измерения q при известных характеристиках РЛС и цели. При наличии оценки потенциала, для расчета ОСШ от объектов наблюдения, находящихся на произвольной дальности, удобно использовать следующую формулу:
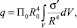(2)
где П0 – оценка потенциала РЛС (величина, численно равная ОСШ от цели с σэфф = 1 м2, находящейся на нормали к антенному полотну, на дальности R0); R – дальность, для которой рассчитывается ОСШ, км.
Выражение (2) с учетом отклонения луча фазированной антенной решетки в азимутальной и угломестной плоскостях от нормали антенны, а также с учетом положения рассеивающего объема относительно максимумов диаграмм направленности антенн принимает вид
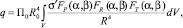(3)
где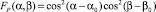 
– функция, учитывающая изменение потенциала в зависимости от отклонения диаграммы направленности от нормали [4]; α0, β0 – значение азимута и угла места, соответствующие максимуму потенциала; α, β – текущие значения азимута и угла места источника сигнала.
Функции, учитывающие изменение величины сигнала в зависимости от положения центра рассеивающего объема относительно максимума диаграммы направленности передающей (приемной) антенн для РЛС с ФАР [6]
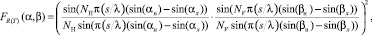
где NH, NV – число излучателей в пределах антенны по горизонтали и вертикали; s – шаг решетки, м; λ – длина волны РЛС, м; αн, βн – углы отклонения центра элементарного объема от нормали; αx, βx – углы отклонения максимума ДН по азимуту и углу места от нормали.
Удельная ЭПР области ионизации [1]
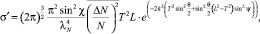
где k = 2π/λ (λ – длина волны РЛС); χ – угол между электрическим вектором падающей волны и волновым вектором рассеянной волны; T – поперечный радиус корреляции (относительно осей x и y), м; L – продольный (относительно оси z) радиус корреляции, м;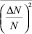 
– средний квадрат флуктуаций электронной концентрации в рассеивающей области; λN – плазменная длина волны, м; θ – угол между волновым вектором падающей и рассеянной волн; ψ – угол между волновым вектором падающей волны и плоскостью, нормальной к оси z (ракурсный угол).
Ракурсный угол ψ определяется по соотношению
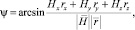
где Hx, Hy, Hz – составляющие геомагнитного поля в точке отражения, соответственно, по осям x, y, z, направленным на север, восток и к центру Земли. Значения Hx, Hy, Hz вычисляются в соответствии с выбранной моделью геомагнитного поля Земли, например IGRF (международное геомагнитное аналитическое поле);
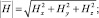
rx, ry, rz – соответствующие составляющие волнового вектора (рассчитываются исходя из координат дислокации РЛС);
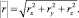
Учитывая, что РЛС ДО регистрируют обратное рассеяние, т.е. χ = 90°, и θ = 180°, имеем
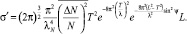(4)
Как видно из (3) и (4), первообразная подынтегральной функции в (3) не выражается через аналитические функции и значения ОСШ могут быть получены численным интегрированием.
Полагая, что величины L, T,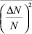 
, λN в пределах объема рассеяния в течение времени облучения имеют постоянное значение, получим
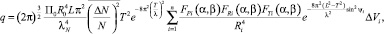(5)
где n – количество элементарных объемов ΔVi, на которые разбивается общий объем рассеяния области ионизации V.
Для оценки сверху величины рассеивающего объема МОН Е-слоя ионосферы можно использовать выражение для разрешенного объема РЛС:
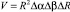, (6)
где R – дальность до центра рассеивающего объема; Δα, Δβ, ΔR – разрешающая способность РЛС по азимуту, углу места, дальности.
Анализ множителя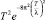 
в (5) показывает, что он вносит существенный вклад лишь для тех значений T2, которые близки к 
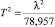, при этом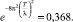 
С учетом сделанного допущения
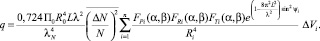(7)
Рассмотрим порядок моделирования функционирования РЛС ДО при воздействии ЕПП, обусловленных МОН Е-слоя ионосферы.
Положение и размеры области рассеяния (АН, МОН Е-слоя среднеширотной ионосферы) в зоне обзора РЛС ДО задаются: географическими координатами центра; продольным и поперечным размерами; высотой и толщиной слоя.
По каждому обнаруженному сигналу в РЛС ДО формируется отметка. Под отметкой понимается набор числовых дискретных характеристик, получаемых обработкой принятых эхо-сигналов. Конкретный набор характеристик, составляющих отметку, зависит от типа РЛС. Как правило, отметка включает оценки дальности, азимута, угла места, амплитуды (мощности) сигнала, а также радиальной скорости для РЛС, производящих измерение доплеровского сдвига частоты принятого сигнала.
При просмотре одного углового направления для каждого измерительного луча по формуле (7) осуществляется расчет ОСШ. Расчеты проводятся с учетом следующих рассуждений.
Размеры элементарных объемов должны выбираться так, чтобы в их пределах ракурсный угол практически не изменялся. Для получения удовлетворительной точности ОСШ угловые размеры ΔVi (по азимуту Δεэ и углу места Δβэ) не должны превышать 0,1°. Исходя из этого в каждом разрешенном элементе по дальности производится разбиение луча на элементарные объемы. Для каждого центра ΔVi осуществляется расчет географических координат и высоты (φ, λ, h). Суммирование в формуле (7) осуществляется по элементарным объемам, у которых центр (φ, λ, h) принадлежит области рассеяния. Величина ΔVi рассчитывается аналогично (6).
Значения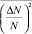 
, λN и L, входящие в формулу (7), могут быть получены в результате обобщения экспериментальных исследований, опубликованных в [3, 5, 8–10].
Плотность распределения вероятностей амплитуды отраженного от АН и МОН среднеширотной ионосферы сигнала описывается законом Рэлея, а мощность экспоненциальным законом [7]. Доплеровское смещение частоты отраженного сигнала (для РЛС ДО, производящих соответствующее измерение), моделируется случайной величиной, имеющей нормальное распределение с нулевым математическим ожиданием и СКО, равным 1 кГц.
Получение оценок азимута и угла места осуществляется в соответствии с алгоритмами работы конкретной РЛС ДО.
На рис. 1 и 2 показаны результаты моделирования отметок в различных плоскостях, при нахождении в зоне действия РЛС ДО двух различных МОН Е-слоя.
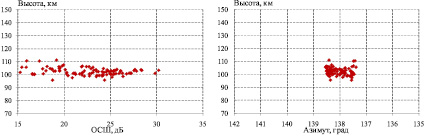
Рис. 1. Результаты моделирования (неоднородность № 1)
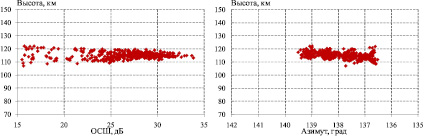
Рис. 2. Результаты моделирования (неоднородность № 2)
Исходные данные по РЛС: координаты точки стояния: 47° с.ш., 47° в.д.; азимут биссектрисы зоны действия 110°; ширина зоны действия по азимуту 120°, по углу места 16°; ширина диаграммы направленности по азимуту 1,5°, по углу места 1,5°; ΔR = 300 м; потенциал РЛС 40 дБ; порог обнаружения 15 дБ; рабочая длина волны РЛС 0,8 м. Для оценки угловых координат в каждой координатной плоскости формируются две перекрещивающиеся диаграммы направленности, разнесенные на одинаковую величину от равносигнального направления – точки пересечения диаграмм (лучей). Величина разнесения лучей равна половине ширины ДН по уровню половинной мощности. Моделировалось 15 циклов просмотра зоны действия.
Параметры ионосферной неоднородности № 1: центр находится в точке с координатами 50,4° с.ш., 58,7 °в.д.; высота 105 км; толщина по высоте 3 км; продольный размер 5 км; поперечный размер 5 км;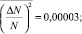 
L = 10 м; λN = 75 м.
Параметры ионосферной неоднородности № 2: центр находится в точке с координатами 50,4 °с.ш., 58,7 °в.д.; высота 117 км; толщина по высоте 3 км; продольный размер 5 км; поперечный размер 25 км;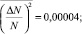 
L = 10 м; λN = 75 м.
Анализ полученных результатов показал, что, варьируя параметрами ионосферных неоднородностей, удается получить параметры отметок, схожие с параметрами, полученными экспериментально в ходе эксплуатации РЛС ДО в условиях воздействия ионосферных помех.
Выводы
Предложенная модель функционирования РЛС ДО в условиях воздействия естественных пассивных помех, обусловленных отражениями от ионосферы, учитывает особенности физических процессов, определяющих специфику их возникновения.
Модель позволяет проводить оценивание алгоритмов работы РЛС ДО в условиях воздействия пассивных помех, обусловленных влиянием ионосферы, и может быть использована при разработке программного обеспечения, предназначенного для проведения испытаний РЛС ДО.