Термин «интерфейс мозг-компьютер» впервые был использован Jacques Vidal [13] для определения любой системы, содержащей компьютер и позволяющей получать информацию о функционировании мозга. На текущий момент можно дать более узкое определение данному понятию. В1999году на первой международной встрече по ИМК сформулировали, что ИМК не должен зависеть от состояния периферийных нервов, доставляющих информацию в мозг или несущих управляющие сигналы от него, а также мышц, управляющих движениями [15].
Спектр задач, на решение которых нацелен интерфейс мозг-компьютер, очень широк. Впервую очередь можно выделить обеспечение альтернативных каналов коммуникации для людей с ограниченными возможностями. Например, написание слов по-средством анализа электроэнцефалографической активности [4], выбор команд на экране монитора из нескольких альтернатив [13], управление протезом на основе интерпретации электроэнцефалографии (ЭЭГ) [11]. Также возможно применение ИМК для общего управления компьютером, что может быть полезно широкой аудитории пользователей, но пока существенных успехов в данной области достичь не удалось, так как для решения этой задачи требуется высокое выходное качество системы. Также в области ИМК можно выделить особую подзадачу – это управление в видеоиграх. Это направление в последнее время получило достаточное широкое распространение, обзор по этой теме может быть найден в [10]. Последней задачей по счету, но не по важности является задача управления техническими системами, например управление роботами и беспилотными летательными аппаратами [9] или создание умного дома [5].
Данная работа посвящена созданию систем для ввода текста на экране монитора на основе компонента P300, а именно различным подходам к классификации сигнала для выявления присутствия/отсутствия компонента в сигнале. Существует множество работ, посвященных задаче классификации компонента P300 для ИМК. Первой из них является работа Donchin и Farwell [6] в 1988году, затем в 2000году авторы улучшили скорость работы системы [4]. С2000г. было проведено множество исследований по классификации компонента P300 для создания систем ИМК для написания текста. Восновном для этой задачи используются линейные методы классификации сигнала, результаты применения которых представлены в [12]. В2003году научной группой Berlin BCI было проведено 3-есоревнование по системам ИМК, одним из наборов данных для соревнования являлся набор с данными для классификации компонента P300 (Data Set II). Врезультате соревнования удалось достичь точности классификации 96 % [12].
В данной работе ставится задача сравнения различных методов извлечения признаков и способов линейной классификации сигнала для выявления присутствия компонента P300 для задачи написания текста на экране монитора.
Компонент P300
Рассмотрим подробнее компонент P300. Название компонента, как и вцелом всех компонентов в нейронауках, состоит из двух частей: P означает positive, 300 означает момент во времени, в котором присутствует компонент. То есть P300 означает положительный пик в окрестности 300-ймиллисекунды (может варьироваться от 250-й до 500-ймс). Схематическое изображение компонента P300 приведено на рис.1.
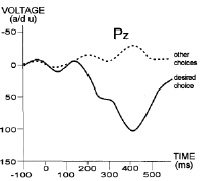
Рис. 1. Компонент P300 [15]
В целом сигнал ЭЭГ представляет собой одномерный сигнал с множества электродов (от 1 до 256), расположенных на поверхности головы. Частота дискретизации сигнала варьируется от нескольких десятков до нескольких сот герц, обычно около 100Гц. Амплитуда сигнала мозговой активности в спокойном состоянии, как правило, не превышает 100мВ.
Для обнаружения компонента P300 целесообразно рассматривать сигнал окрестности 300мс, в частности принято рассматривать сигнал в диапазоне от 0мс (момент атаки внешнего стимула) до 600–800мс, вплоть до 1с. Таким образом, сигнал при частоте дискретизации 100Гц и наличии 64электродов и интервале в 1снасчитывает 6400отсчетов по времени.
Набор данных
В данной работе мы использовали набор данных с соревнований по ИМК (BCI Competition III), организованных группой Berlin BCI. Данные для соревнования были предоставлены научной группой по ИМК университета г.Грац (Австрия).
Набор данных представляет собой сигналы ЭЭГ, записанные с применением системы BCI 2000 [2] и использованием 64электродов при частоте дискретизации 240Гц. Данные были предобработаны частотным фильтром с пропускающим диапазоном 0,1–60Гц.
Набор данных был записан в ходе эксперимента по вводу текста на основе парадигмы P300 от двух пользователей. Рассмотрим подробнее процедуру эксперимента. Пользователю предъявлялась матрица символов размером 6×6 (рис.2). Пользователь должен был фокусироваться на желаемой букве. Все строки и колонки матрицы поочередно вспыхивали в случайном порядке. Двум из 12вспышек соответствовал желаемый символ (строка и колонка). Вмомент вспышки желаемых символов в электроэнцефалограмме пользователя регистрировался компонент P300.
Рис. 2. Матрица символов для набора текста с использованием ИМК на основе P300
Подсветка строк и колонок производилась согласно следующей процедуре. Вначальный момент времени матрица отображалась без подсветки символов в течение 2,5секунд. Затем каждая строка и колонка подсвечивалась в течение 100мс. Интервал между вспышками – 75мс. Такая процедура повторялась 15раз для каждого символа. Пауза между символами – 2,5секунды.
Набор данных содержит две выборки – обучающую и тестовую. Обучающая выборка состоит из 100букв, тестовая – из 85. Таким образом, для каждого участника эксперимента было записано 185букв.
Методы извлечения признаков
Использование исходного сигнала
Наиболее простым и очевидным методом анализа сигнала является использование его в исходном виде, но данный подход обладает рядом недостатков. Во-первых, если использовать исходный сигнал без предварительного извлечения признаков, то размерность пространства данных будет очень высока, что ухудшает работу классификаторов. Во-вторых, исходный сигнал содержит избыточную информацию, которая также ухудшает качество классификации. Избыточная информация содержится как во временном измерении, так и впространстве электродов. В-третьих, часть исходного сигнала практически не содержит дискриминативной информации, что также приводит к ухудшению точности классификации. Это актуально как для временного пространства, так и для пространства электродов. Например, сигнал с 0–50мс и с 800–1000мс содержит меньше всего дискриминативной информации.
Усреднение сигнала
Альтернативой использования исходного сигнала является усреднение сигнала, то есть замена нескольких последовательных значений амплитуд сигнала их средним значением. Это позволяет сохранить форму сигнала, при этом устранив высокочастотные колебания и уменьшив количество значений амплитуд сигнала. Внекоторых случаях, например при классификации представляемых движений, такой подход неприменим, так как в высокочастотных колебаниях содержится значимая для этой задачи информация. Вслучае компонента P300 для детекции пика в районе 300мс важна именно форма сигнала, поэтому усреднение дает положительные результаты.
Для усреднения сигнала применяется оконная функция, в рамках которой происходит нахождение среднего значения сигнала, затем исходный сигнал заменяется вычисленными средними значениями. Оконная функция может применяться как с шагом равным размеру окна, так и с произвольным шагом, например равным половине окна. Во втором случае окна перекрываются между собой, что позволяет сохранить больше информации в сигнале, добавив таким образом некоторую избыточность. Также возможен вариант не прямоугольной оконной функции, а взвешенной, например треугольной.
Метод главных компонент
Метод главных компонент (Principle Component Analysis, PCA) позволяет снизить размерность исходного вектора данных на основе проекции исходного пространства данных в пространство, составленное из собственных векторов, упорядоченных по соответствующим собственным числам. Первые n проекций представляют собой наиболее значимые компоненты, имеющие наибольшую дисперсию. Соответственно, снизить размерность исходного пространства можно используя первые n компонент. Математически это можно выразить следующим образом [7]:
Пусть X – входной сигнал в виде матрицы размерности n×m, где n – число измерений сигнала, m – число отсчетов по времени в каждом измерении. Пусть R – ковариационная матрица размерности m×m, определяемая выражением
R=E[XTX], (1)
где E – математическое ожидание.
Пусть λ – вектор размерности m, состоящий из собственных чисел матрицы R, а Q – матрица размерности m×m, состоящая из собственных векторов матрицы R, соответствующих собственным числам λ. Собственные вектора являются ортогональными, поэтому, выполнив проекцию исходных данных на пространство собственных векторов, получаем матрицу данных, компоненты которой являются некоррелированными:
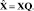(2)
Тем самым мы осуществили переход в новое пространство собственных векторов матрицы R, собственные же значения матрицы R выражают дисперсии данных по соответствующим собственным векторам. Чем больше дисперсия, тем более значимым является собственный вектор. Упорядочив собственные значения λ по убыванию, так чтобы λ1> λ2>...> λn и переупорядочив соответственно собственные вектора qi матрицы Q, можно снизить размерность исходного пространства, выбрав первые l векторов, которые будут отражать наиболее значимые компоненты данных. Это можно записать в виде
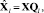(3)
где Ql – матрица из l собственных векторов (l<n), которые упорядочены по убыванию соответствующих собственных значений;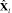 
– l главных компонент исходных данных X.
Более подробное описание метода главных компонент приведено в [7].
Выбор электродов
Как известно, головной мозг делится на несколько зон в зависимости от функционального назначения. Поэтому целесообразно производить отбор электродов для регистрации данных при выполнении той или иной задачи. Вчастности, обработке визуальной информации соответствует затылочная часть коры головного мозга.
В данной работе мы используем именно визуальные стимулы, поэтому представляется целесообразным использование Fz, Pz, Cz, Oz, P3, C3, P4, C4, PO7 и PO8 электродов по классификации 10–20 [8].
Также уменьшение числа используемых электродов приводит к снижению размерности исходного пространства данных, что положительно сказывается на результатах классификации при условии сохранения значимой информации. Так как сигналы соседних электродов сильно коррелированы, то значительных потерь информации можно избежать при правильном выборе электродов.
Методы классификации сигнала
Машина опорных векторов
Машина опорных векторов – метод классификации, который разделяет классы посредством максимизации расстояния между разделяющей классы гиперплоскостью и объектами этих классов, с помощью построения так называемых линейных векторов, при этом образуется зазор между классами максимально возможной ширины. Метод был предложен Вапником и Червоненкисом [3].
Пусть имеются два линейно разделимых класса. Необходимо найти гиперплоскость, которая разделит эти два класса оптимально. Оптимальной гиперплоскостью будем считать ту гиперплоскость, которая максимизирует расстояние от нее до ближайшей точки обучающей выборки.
Разделяющая гиперплоскость имеет вид
wx – b=0, (4)
где w – перпендикуляр к разделяющей гиперплоскости.
Параметр 
равен расстоянию от гиперплоскости до начала координат [3]. Положим единичный зазор по обе стороны от разделяющей гиперплоскости, эти гиперплоскости будут параллельны разделяющей и иметь вид
wx – b=1, (5)
wx – b= –1. (6)
Расстояние между ними будет равняться 
, такие гиперплоскости называются опорными. Ближайшие точки к опорным гиперплоскостям (или лежащие на них) называются опорными векторами.
Построение классификатора состоит в отыскании разделяющей гиперплоскости с учетом выполнения требования, чтобы все точки лежали по разные стороны опорных гиперплоскостей. Это может быть записано в виде
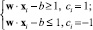(7)
или
ci(w•xi – b) ≥ 1; 1<i<n, (8)
где n – число объектов обучающей выборки.
Проблема построения разделяющей гиперплоскости сводится к минимизации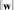 
при условии (8):
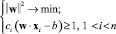. (9)
Решение данной задачи может быть найдено при помощи методов квадратичной оптимизации. Более подробное описание изложенного метода приведено в [3].
Линейный дискриминантный анализ
Дискриминантный анализ проецирует пространство данных в пространство более низкой размерности с учетом минимизации дисперсии классов и максимизации межклассовых расстояний.
Математически это можно выразить следующим образом:
Пусть x – вектор объектов; w – разделяющая прямая, тогда результат линейной классификации может быть выражен как [1]:
y=wTx. (10)
Пусть m1 – центр масс первого класса; m2 – центр масс второго класса. Для максимизации расстояния между классами будем проектировать классы на вектор, соединяющий центры масс:
w ∞ m2 – m1. (11)
Выразим дисперсии внутри классов:
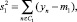(12)
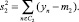(13)
И потребуем минимизации дисперсии, что может быть выражено через максимизацию целевой функции Фишера:
(14)
Числитель дроби максимизирует расстояние между классами, а знаменатель минимизирует дисперсию внутри классов. Выполнив оптимизацию J(w), получаем искомую разделяющую прямую w. Более подробное описание линейного дискриминантного анализа может быть найдено в [1].
Комитетные методы классификации
Комитетные методы классификации позволяют принимать решения о принадлежности объекта к тому или иному классу на основе использования нескольких классификаторов. Два основных способа построения таких комитетов (или ансамблей) классификаторов: бэггинг (bagging) и бустинг (boosting) [1].
Бэггинг заключается в обучении классификаторов на различных наборах данных, разбивая исходную обучающую выборку на несколько непересекающихся частей. Окончательное решение принимается путем усреднения ответов классификаторов, входящих в состав ансамбля.
В методе бустинга классификаторы обучаются последовательно. Обучение m-гоклас-сификатора зависит от результатов обучения m – 1 классификаторов. При обучении классификатора наибольшее внимание уделяется тем объектам в обучающей выборке, на которых предыдущие классификаторы допускали ошибки. После обучения ансамбля классификаторов окончательное решение принимается путем взвешенного голосования, причем вес классификаторов определяется на основе результатов обучения, то есть на основе степени доверия к классификатору.
Анализ результатов численных экспериментов
Исходный сигнал
В таблице представлены результаты классификации с использованием исходного сигнала для полного и частичного набора электродов. Для получения более отчетливого отклика P300 при тестировании результатов производилось усреднение сигнала по 15попыткам для каждой буквы (см. описание набора данных). При обучении классификатора усреднение сигнала не производилось. Такой подход использовался для всех полученных результатов. Все последующие результаты представлены для первого субъекта в исходном наборе данных.
Как можно видеть, наилучшая точность 71 % была получена при использовании LDA в качестве классификатора и 10электродов.
Результат классификации исходного сигнала (точность, %)
|
Классификатор Кол-во электродов |
LDA |
SVM |
|
64 |
41 |
68 |
|
10 |
71 |
13 |
Метод главных компонент
На рис.3 приведены результаты тестирования с использованием метода главных компонент для двух классификаторов и двух наборов электродов. Наилучший результат 89 % был получен при использовании 300главных компонент, полного набора электродов и LDA классификатора.
Усреднение сигнала
На рис.4 приведена зависимость точности распознавания от количества диапазонов, в рамках которых производилось усреднение сигнала. Из рисунка видно, что LDA значительно превосходит SVM, наилучшая точность 90 % была получена при использовании LDA классификатора и 14диапазонов усреднения. Результаты представлены только для набора из 10электродов, по причине низкой производительности классификаторов на большом числе признаков.
Комитетные методы классификации
Далее представлены результаты с использованием комитетных методов классификации и усреднения сигнала. На рис.5 изображена зависимость точности распознавания от числа классификаторов в ансамбле. Входе экспериментов было проанализировано использование различного числа диапазонов усреднения, на рис.6 отражены лучшие результаты. Для LDA использовалось 20диапазонов, SVM-14. Данные представлены для набора из 10электродов.
Для построения ансамбля классификаторов мы использовали метод бэггинг. Так как тестовая выборка состояла из 85букв, то все данные были разбиты на части по 1, 3, 5, 10, 15, 20, 25, 40букв в каждой. Были получены ансамбли, состоящие из 85, 29, 17, 9, 6, 5, 4, 3 классификаторов соответственно, каждый из них обучался на своей подвыборке, затем результат классификаторов усреднялся. Вслучае если общее число букв не делится на число классификаторов нацело, то последний классификатор обучался на подвыборке меньшего размера, полученной как остаток от деления. Наилучшая точность 93 % была получена при построении ансамбля из 9-ти LDA классификаторов.
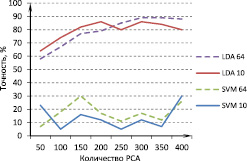
Рис. 3. Зависимость точности распознавания от количества главных компонент
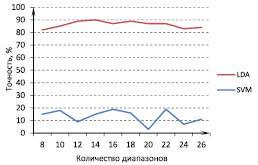
Рис. 4. Зависимость точности распознавания с применением усреднения сигнала (10электродов)
Рис. 5. Зависимость точности распознавания от размера комитета
По результатам экспериментов наилучшая точность и устойчивость была получена при использовании комбинации методов предобработки. Метод главных компонент был применен к пространству 64электродов, тем самым снижая размерность исходного пространства, затем мы применили усреднение сигнала во времени с использованием 20диапазонов и шагом перекрытия3. Также мы использовали комитетный метод с 9классификаторами. Лучшая точность 100 % была получена при использовании LDA и 40главных компонент. На рис.4 представлена зависимость точности классификации от количества используемых главных компонент. Для сравнения показаны результаты с использованием SVM.
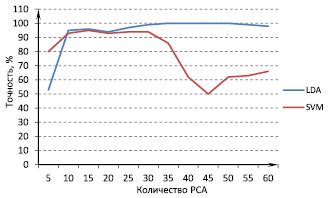
Рис. 6. Зависимость точности распознавания от количества PCAс применением усреднения сигнала
Разработанный метод с данными параметрами был применен также и для второго субъекта в наборе данных, для него была достигнута точность распознавания 98 %.
Выводы
В данной статье была рассмотрена задача обнаружения компонента P300 в ЭЭГ сигнале. Были проанализированы различные способы извлечения признаков сигнала, возможность выбора электродов и применения разных классификаторов. По итогам проведенных экспериментов можно сделать следующие выводы:
Во-первых, из полученных результатов видно, что использование исходного сигнала без снижения размерности дает невысокую точность. Лучшая точность равная 71 % достигается при использовании LDA и 10электродов.
Во-вторых, использование методов снижения размерности, таких как метод главных компонент или усреднение сигнала, повышает точность, в лучшем случае до 90 %.
В-третьих, использование LDA классификатора позволяет получить более высокую точность в сравнении с SVM. Также LDA лучше справляется с пространствами более высокой размерности в данной задаче, нежели SVM.
В-четвертых, использование комитетных методов классификации также повышает точность распознавания. Влучшем случае удалось достичь точности 93 % при использовании 9-ти LDA классификаторов, 20диапазонов усреднения и 10 электродов.
По итогам экспериментов наилучшая точность была достигнута на 64электродах при использовании комбинации методов: главных компонент (примененного к пространству электродов), усреднения с перекрытием диапазонов и комитета из LDA классификаторов. Точность классификации составила 100 и 98 % для первого и для второго субъекта соответ-ственно.