На сегодняшний день использование термина «хаос» в научных исследованиях связано с необходимостью описания таких систем, которые характеризуются совершенно случайной, на первый взгляд, динамикой и в то же время присутствием в них скрытого порядка.
Достаточно актуальная научная проблема управления хаотической динамикой не решена и в настоящее время. Из большого количества имеющихся аспектов ее решения в качестве чрезвычайно важного можно выделить исследование разнообразных методов и законов, подавляющих нерегулярные колебания в нелинейных системах, которые характеризуются наличием хаотической динамики [1, 4–5].
Проблематика управления нелинейными системами с хаотической динамикой имеет важное прикладное значение. Стоит отметить, что дело здесь не только в борьбе с хаосом, который зачастую нарушает качество функционирования сложных систем, но и в целесообразной для ряда технологических процессов идее возникновения так называемого «порядка из хаоса» [2].
Проблема подавления нерегулярных колебаний относится к наиболее характерным проблемам управления моделями с хаотической динамикой и состоит в таком формировании управляющих воздействий, при котором обеспечивается стабилизация изначально хаотической модели в устойчивом стационарном состоянии. В дальнейшем полагается, что имеется возможность влияния на динамику модели с помощью некоторого внешнего управляющего воздействия, которое аддитивно входит в состав правой части одного из ее дифференциальных уравнений.
Цель исследования. В данной работе решена задача построения скалярных законов управления, которые обеспечивают подавление хаотических колебаний в типовых хаотических системах Лоренца и Ресслера, при которых происходит стабилизация нерегулярных колебаний исходных моделей в равновесном устойчивом состоянии. Задачи аналогичного типа возникают в случае необходимости устранить нежелательные вибрации конструкций, различные шумы и т.д. [1, 4].
Материалы и методы исследования
Одним из методов эффективного решения сложной задачи управления хаосом и синтеза объективных законов управления нелинейными системами с хаотической динамикой является метод аналитического конструирования агрегированных регуляторов (АКАР), предложенный профессором А.А. Колесниковым [3].
Построение скалярных регуляторов методом аналитического конструирования агрегированных регуляторов основывается на введении последовательности инвариантных многообразий понижающейся геометрической размерности и последующей поэтапной динамической декомпозиции исходной динамической системы. В таком случае изображающая точка (ИТ) системы, начав двигаться из произвольного начального состояния, последовательно перемещается от одной поверхности притяжения к другой, пока не попадет на финишную поверхность вида ψ1 = 0 → ψ2 = 0 → ... → ψm = 0. «Внутренние» многообразия топологически вкладываются во «внешние». Таким образом, в синтезируемой системе возникает внутренний процесс самоуправления. В результате происходит каскадное формирование последовательности внутренних управлений, которые сжимают фазовый объем системы по направлению от внешней области фазового пространства к совокупности вкладываемых друг в друга внутренних областей вплоть до попадания ИТ в желаемое состояние системы.
Допустим, что в пространстве состояний замкнутой системы существует притягивающее инвариантное многообразие вида ψ(x) = 0, являющееся асимптотическим пределом фазовых траекторий. Вообще, подобных многообразий может быть несколько. Как правило, количество инвариантных многообразий совпадает с количеством каналов управления. Тогда изображающая точка системы начинает стремиться к пересечению инвариантных многообразий. Необходимым условием попадания изображающей точки замкнутой системы «объект-регулятор» на инвариантное многообразие ψ(x) = 0 является, чтобы ее движение удовлетворяло некоторому устойчивому дифференциальному уравнению, записанному относительно агрегированной макропеременной ψ(x). Такое уравнение в синергетической теории управления называют функциональным или эволюционным. Обычно система функциональных уравнений задается как система обыкновенных дифференциальных уравнений первого порядка вида
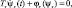s = 1, 2, ..., m, Ts > 0.
Здесь m – число заданных инвариантных многообразий; Ts – управляющий параметр, φs(ψs) – функция, которая должна удовлетворять следующей совокупности условий:
1) φs(ψs) должна быть непрерывна, однозначна и дифференцируема при всех ψs;
2) φs(0) = 0;
3) φs(ψs) > 0 при любых 0,
т.е. они обращаются в нуль только на многообразиях φs = 0, относительно которых система заданных функциональных уравнений асимптотически устойчива в целом.
Как правило, в методе АКАР используются функциональные уравнения:
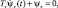
т.е. φs(ψs) = ψs0. Уравнения такого типа, как видно, характеризуются асимптотической устойчивостью относительно многообразия ψs = 0 при условии Ts > 0.
В данной ситуации задача синтеза законов стабилизирующего управления хаотическими моделями в общем случае формулируется следующим образом. Необходимо найти функцию uS(x) как некоторую совокупность обратных связей, обеспечивающих перевод изображающей точки исходной хаотической модели из произвольных начальных условий в некоторой допустимой области в заданное состояние (совокупность состояний), которое соответствует устойчивому режиму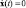 
. В самом простом случае управление входит только в одно дифференциальное уравнение исходной системы. Могут быть варианты, когда одно и то же управляющее воздействие находится в разных строках исходной системы [6].
Отличительным аспектом постановки задачи синергетического синтеза законов управления является наличие дополнительного требования к движению системы из начального состояния в конечное, которое состоит в асимптотическом притягивании фазовых траекторий системы к некоторому инвариантному многообразию (пересечению многообразий) в пространстве состояний (ПС) системы.
Введение в уравнения исходной модели стабилизирующей обратной связи приводит к целенаправленному изменению топологии ее пространства состояний. Вследствие подобной перестройки происходит исчезновение хаотического аттрактора и формирование регулярного аттрактора типа «точка», который соответствуют желаемому равновесному режиму поведения.
Результаты исследования и их обсуждение
Рассмотрим этапы реализованной процедуры синтеза стабилизирующего закона управления методом АКАР для хаотической системы Лоренца.
Модель Лоренца была первоначально получена из уравнений Навье - Стокса и теплопроводности с целью исследования возможности прогнозирования погодных условий при вариации управляющих параметров. Модель описывает движение конвективных валов в жидкости при температурном градиенте.
Модель представляет собой следующую систему трех обыкновенных дифференциальных уравнений [7]:
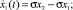
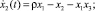(1)
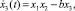
где σ – число Прандтля; ρ – нормированное число Рэлея; параметр b зависит от взаимоудаленности плоскостей и горизонтального периода.
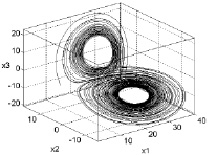
Рис. 1. Хаотический аттрактор системы Лоренца
В этой системе при определенных условиях происходит формирование хаотических колебаний. На рис. 1 показана фазовая траектория системы при значениях параметров σ = 10, ρ = 24, b = 8/3 в режиме детерминированного хаоса. В данной динамической системе впервые исследовались стохастические автоколебания. Хаотический аттрактор системы (1) принципиально отличается от хаотических аттракторов большинства моделей нелинейной динамики. Его структура полностью соответствует странному аттрактору и характеризуется наличием лишь седлового типа движения.
Предположим, что управляющее воздействие u1 входит в первое уравнение системы (1) в виде внутренней обратной связи:
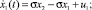
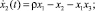(2)
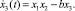
Введем одно инвариантное многообразие вида
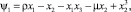(3)
где μ – некоторый управляющий параметр.
Если продифференцировать функцию ψ1 (3) по времени и подставить ее производную в функциональное уравнение
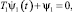(4)
мы получим искомый закон управления:
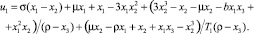(5)
Закон управления (5) обеспечивает перевод изображающей точки системы (2), замкнутой обратной связью (5), на инвариантное многообразие ψ1 = 0.
Динамика движения изображающей точки модели по данному инвариантному многообразию описывается с помощью дифференциальных уравнений декомпозированной модели, которые образуются после подстановки выражения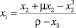 
из равенства ψ1 = 0 (3) во второе и третье уравнения системы (2):
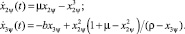(6)
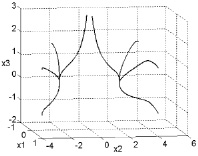
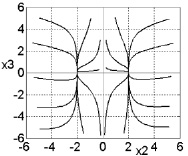
Рис. 2. Фазовые портреты систем (2), (5) и (6)
Рис. 2 иллюстрирует результаты проведенного численного моделирования системы (2), (5) при значениях управляющих параметров σ = 10, ρ = 24, b = 8/3, характерных для существования хаотического аттрактора Лоренца, и значениях параметров регулятора T1 = 0,1, μ = 4, которые подтверждают эффективность теоретических положений метода АКАР. Первое уравнение в декомпозированной системе (6) полностью идентично базовому эволюционному уравнению синергетики с бифуркацией типа «вилка».
Проведем построение стабилизирующего закона управления методом АКАР для модели Ресслера. Модель Ресслера – это нелинейная динамическая система дифференциальных уравнений третьего порядка вида [8]:
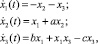(7)
где a, b, c – управляющие параметры.
Система (7) была предложена Ресслером для моделирования процессов взаимодействия ряда химических веществ. Данная система достаточно часто применяется в разнообразных научных исследованиях явлений разнообразной природы в связи с наличием характерных для них признаков появления и существования хаотической динамики. Рис. 3 демонстрирует хаотический аттрактор системы Ресслера при значениях параметров a = b = 0,2; c = 9.
Допустим, что управляющее воздействие входит во второе уравнение исходной системы (7):
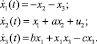(8)
Вид инвариантного многообразия
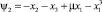(9)
и функциональное уравнение (4) позволяют получить искомый закон управления:
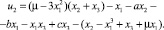(10)
Закон управления (10) гарантирует перевод изображающей точки управляемой системы (8), которая замкнута обратной связью (10), на инвариантное многообразие ψ2 = 0 (9).
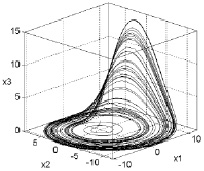
Рис. 3. Хаотический аттрактор системы Ресслера
Характер движения системы вдоль инвариантного многообразия ψ2 = 0 описывает декомпозированная модель:
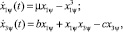(11)
где уравнение бифуркации типа «вилка» присутствует в первой строке.
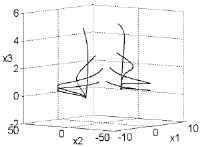
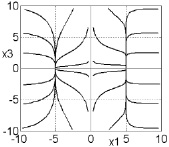
Рис. 4. Фазовые портреты систем (8), (10) и (11)
Рис. 4 иллюстрирует полученные результаты численного моделирования замкнутой системы (8), (10) для значений управляющих параметров модели a = b = 0,2; c = 9, которые характерны для возникновения аттрактора хаотического типа, а также значений параметров регулятора T2 = 0,1; μ = 25.
Выводы
В обеих полученных декомпозированных моделях (6), (11) уравнения, расположенные в первой строке, совпадают с базовым эволюционным уравнением синергетики с бифуркацией типа «вилка». В связи с этим мы можем утверждать о естественном характере синтезированных законов стабилизирующего управления исходными хаотическими системами и о имеющемся единстве и внутренней взаимосвязи универсальных эволюционных уравнений нелинейной теории самоорганизации и синергетики.
Естественный характер синтезированных управляющих законов обусловлен, прежде всего, наличием у замкнутых систем совокупности типичных бифуркационных свойств.
В результате проведенного исследования синтезирована совокупность обратных связей, при замыкании которыми исходных хаотических систем возникает изменение характера их поведения и трансформация аттрактора хаотического типа в аттрактор типа «точка». Полученные законы управления u1 (5) и u2 (10) гарантированно обеспечивают асимптотическую устойчивость во всем фазовом пространстве относительно желаемых состояний равновесия при значениях параметра μ < 0 или μ > 0 для соответствующих исходных хаотических моделей. Полученные законы u1 (5) и u2 (10) принадлежат к классу объективных законов управления, преобразовывающих системы Лоренца и Ресслера, обладающие хаотической динамикой, в базовые эволюционные уравнения теории самоорганизации и синергетики.
Синтезированные законы управления u1 (5) и u2 (10) оригинальны и универсальны. Они могут применяться при проектировании управляемых систем разнообразного назначения, значительно повышая эффективность их функционирования.