Процесс производства металлопродукции является длительным многоступенчатым процессом. Важной задачей является отслеживание движения металла по технологической цепочке с учетом изменения его параметров и фиксацией параметров обработки на отдельных агрегатах, что формирует состояние клеток итеративной сети, описывающих эти агрегаты. Движение металла по агрегатам, используемое в итеративных сетях [1–5], приведено на рис. 1.
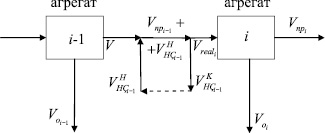
Рис. 1. Движение металла между агрегатами
Входом для каждого i-го агрегата в представленной модели является величина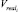 
, показывающая, какой объем продукции в состоянии обработать данное оборудование за текущий период (в данном случае месяц). Данная величина может быть получена в результате объемного планирования и распределения производственной программы по календарным периодам. Вход 
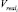является составным и складывается из суммарных значений объема годной продукции, произведенной на i – 1-м агрегате, и количества незавершенного производства, находящегося на складе, на начало текущего календарного периода. Однако не весь объем поставляемых полуфабрикатов может быть обработан на следующем переделе из-за ограничений по мощности оборудования, оставшаяся часть годного сырья поступает на склады и составляет незавершенное производство на начало следующего отрезка времени.
Выходами элементарной ячейки технологической цепи служат неотъемлемые составляющие любого производства: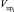 
– годная продукция, подлежащая обработке на следующем производственном агрегате; 
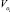– отходы производства, включающие также полуфабрикаты, забракованные отделом технического контроля и направленные в беззаказную продукцию.
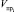– объем годного полуфабриката после i-го агрегата; 
, 
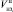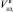– объем незавершенного производства после i-го агрегата (начало и конец месяца); 
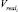– объем полуфабриката, обработанного на i-м агрегате (за исследуемый календарный период).
Описать изменение себестоимости продукции можно с помощью итеративных сетей. Наиболее удобным является использование одномерных двунаправленных итеративных сетей. Применение таких сетей позволяет учесть незавершенное производство металла от агрегата к агрегату в течение длительного времени за счет наличия временной переменной.
Итеративная сеть представляет собой цепочку клеток с памятью [1, 3]. Сигналы в такой сети зависят не только от номера клеток s, но и от времени t. Обозначим состояние клетки s в момент t через ξ(t, s). Кроме внешних входа u(t, s) и выхода y(t, s), она имеет внутренние вход x(t, s – 1) и выход x(t, s).
Величины, представленные выше, необходимо описать в терминах одномерных двунаправленных сетей.
Для каждого состояния необходимо ввести дополнительные индексы:
i – номер агрегата (i = 1, …, n), j – номер элемента сортамента (j = 1, …, m); t – календарный период.
Номер клетки s определяется индексом, соответствующим номеру агрегата технологической цепи. Таким образом, каждая s{i} клетка итеративной сети описания производства будет иметь, помимо состояний ξ(t, s{i}), внутренние входы x(t, s{i – 1}) и выход x(t, s{i}).
В итоге с помощью внутренних состояний и внутренних входов и выходов можно описать основные переменные:
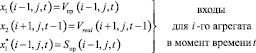
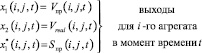
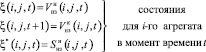
Каждый i-й агрегат за рассматриваемый календарный период t должен произвести определенный объем продукции Vпр(i, j, t), которая должна быть направлена на обработку на следующий i + 1-й агрегат либо отправлена в складские помещения в качестве незавершенного производства, добавляемого к уже хранящемуся на начало текущего месяца объему сырья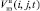 
.
Причем текущая себестоимость полуфабрикатов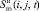 
может отличаться от себестоимости на продукцию за предыдущие отрезки рассматриваемого календарного периода.
Продукция может ожидать дальнейшей обработки продолжительное время. Если по истечении исследуемого отрезка календарного периода суммарные заказы Vreal(i + 1, j, t – 1) на полуфабрикаты от следующего в цепи агрегата уступают в размере находящемуся на хранении на начало текущего момента времени объему металлов, то на начало следующего месяца на складе останется объем полуфабрикатов, равный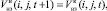 
определяемый как разность двух величин:
– количества годной продукции, поступающей напрямую с i-го агрегата, и объема хранящегося на складах незавершенного производства, т.е.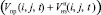 
;
– объема полуфабриката, обработанного на i + 1-м агрегате за истекший месяц Vreal(i + 1, j, t – 1).
В качестве внутреннего входа для i-го оборудования выбрана величина Vreal(i + 1, j, t – 1), которая характеризует фактическую мощность i + 1-го металлургического агрегата и показывает, какое количество полуфабрикатов агрегат действительно может обработать без увеличения текущей его загрузки при учете трудоемкости операций. Требуемый объем может рассчитываться в результате решения задачи объемно-календарного планирования по критерию минимизации суммарных издержек на хранение полуфабрикатов, длительности производственного цикла получения заданного объема готовой продукции. В результате учета величины Vreal(i + 1, j, t – 1) затраты предприятия на незавершенное производство не будут превосходить заданного уровня расходов.
Как было отмечено выше, расчет себестоимости готовой продукции происходит итеративно по всем видам оборудования. При расчете стоимости полуфабрикатов на каждом i + 1-м этапе требуется размер цены Sпр(i, j, t) годного продукта, обработанного за предыдущую операцию.
Одномерная двунаправленная итеративная сеть, описывающая движение металла с учетом стоимости полуфабриката, представлена на рис. 2, где X1, X2, Ξ, Ξ* – векторы, учитывающие обрабатываемый сортамент:
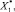
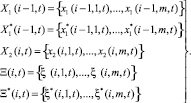
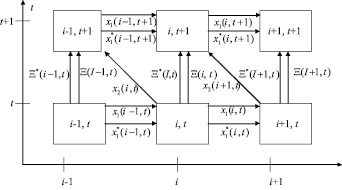
Рис. 2. Одномерная двунаправленная итеративная сеть движения металла с учетом стоимости полуфабриката
Управление данной сетью можно представить в виде
В общем виде для задачи расчета себестоимости металлопродукции на основе модели итеративных сетей уравнения состояний и внутренних входов и выходов клетки с памятью, или обычной линейной стационарной дискретно-временной динамической системы, могут быть представлены в следующей форме:
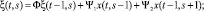
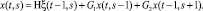
Это описание формально вполне идентично описанию двумерной полуторанаправленной цепи [1, 3]. Шаблон пространственно-временного соседства соответствует показанному на рис. 3.
Рассмотрим один из вариантов двумерных полуторанаправленных итеративных цепей, для простоты представленного только шаблоном соседства.
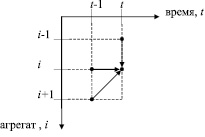
Рис. 3. Шаблон соседства двумерной полуторанаправленной цепи
Данная цепь описывается уравнением
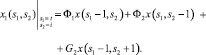
Таким образом, итеративная сеть как дискретная пространственно-временная модель, выбранная для расчета себестоимости металлопродукции, позволяет решать одну из основных проблем, возникающих при производстве продукции с появлением незавершенного производства, – необходимость учитывать в течение некоторого календарного периода разницу в затратах на обработку полуфабрикатов, хранящихся на складе, и корректно переносить ее в себестоимость готовой продукции.
Заключение
С помощью клеток с памятью итеративной сети можно описывать движение металла по переделам и агрегатам за исследуемый период времени. При этом анализ не ограничивается единичным календарным отрезком времени (например, месяцем). Итеративная сеть позволяет отслеживать информацию о производстве и себестоимости производимой продукции в динамике. Учитывается стоимость годного полуфабриката, обработанного каждым агрегатом, стоимость незавершенного производства на начало периода, объем годного полуфабриката и незавершенного производства после каждого агрегата (начало и конец месяца) в течение длительного периода времени, разбитого на единичные отрезки времени.