Создание систем вторичного подрессоривания автомобильного транспорта с заданными виброзащитными свойствами определяет необходимость разработки таких виброизоляторов, которые смогут обеспечить оптимальную виброзащиту в конкретных динамических системах. Выбор оптимальных конструктивных параметров пневматического упругого элемента с резино-кордными оболочками (РКО) тороидного типа зависит от требований, предъявляемых, прежде всего, к эффективности функционирования пневмоэлемента в системе подвешивания объекта виброзащиты. Эти требования обычно сводят к некоторому вектору качества системы и условиям работоспособности, определяемым в техническом задании на проектирование. Задачи виброзащиты требуют создания систем с наперёд заданной силовой характеристикой, которая обеспечивает требуемое снижение уровня вибрации. При использовании резино-кордных оболочек тороидного типа возможно получение желаемых законов изменения рабочих характеристик оболочки, а следовательно, и желаемой характеристики упругого элемента [6].
Одной из главных динамических характеристик, определяющих упруго-диссипативные свойства любой виброзащитной опоры, является зависимость силовой функции от его прогиба – нагрузочная характеристика. На формирование упруго-диссипативных свойств пневматических упругих элементов с РКО тороидного типа существенное влияние оказывает целый ряд конструктивных параметров, к которым относятся параметры, задающиеся при проектировании упругого элемента с РКО [7]. Огромное количество этих факторов не позволяет произвести полный анализ физического процесса при работе пневматического упругого элемента с РКО тороидного типа, поэтому возникает необходимость ограничиться наиболее существенными из них [3].
Задачей проектирования оптимальных систем вторичного подрессоривания является обеспечение реализации требуемых низких собственных частот колебаний объекта виброзащиты при минимальных перемещениях его относительно основания и других, сопряженных с объектом, узлов и агрегатов, что особенно важно для кабин транспортно-технологических комплексов, для которых проблема уменьшения допустимых перемещений по всем направлениям колебаний стоит особенно остро.
В процессе эксплуатации подрессоренная кабина транспортно-технологического комплекса совершает сложные пространственные движения. Пневматические упругие элементы с РКО тороидного типа в системе вторичного подрессоривания испытывают как осевые, так и продольные и поперечные внешние воздействия. Наряду с этим кабина транспортного средства компоновочно связана со многими агрегатами и системами машины, поэтому при разработке конструкции системы вторичного подрессоривания необходимо стремиться к уменьшению её перемещений относительно рамы, двигателя, а также перевозимых грузов и других агрегатов, чтобы создать минимально необходимые зазоры в местах возможных контактов [8, 9].
Разработанный метод расчёта геометрии направляющих поверхностей металлоарматуры упругих элементов с РКО был положен в основу при разработке конструкции пневматического виброизолятора с РКО тороидного типа для систем вторичного подрессоривания [5, 1].
Текущее значение усилия Q(x) на пневматический упругий элемент с РКО тороидного типа определяется по уравнениям
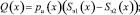(1)
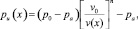(2)
где pu(x) – текущее значение давления в РКО; Sэ1(x), Sэ2(x) – текущее значение эффективных площадей верхнего и нижнего гофров РКО тороидного типа; p0 – начальное (статическое) значение давления в РКО; pa – атмосферное давление; V0 – начальный объем внутренней полости РКО; V(x) – текущее значение объема внутренней полости РКО; n – показатель политропы, зависящий от условий теплообмена между рабочим газом и окружающей средой [2].
Значение текущего объёма определяется после разбиения суммарного объёма на элементарные составляющие, объём которых вычисляется по теореме Гюльдена:
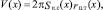(3)
где Sп.с(x) – площадь поперечного сечения фигуры вращения; rц.т(x) – координаты центра тяжести фигуры вращения.
Дифференцируя по x уравнение (1), получим формулу для определения осевой жесткости Cx пневмоамортизатора:
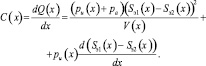
Эта формула показывает, что осевая жесткость пневмоамортизатора определяется суммой двух слагаемых, из которых первое зависит от размеров пневматического упругого элемента (т.е. от величин Sэ1(x) и Sэ2(x) и от показателя политропы воздуха, а второе зависит еще и от скорости изменения эффективного радиуса, то есть от формы направляющих поверхностей металлоарматуры [6, 7].
Геометрические параметры пневматического упругого элемента с РКО тороидного типа, влияющие на его характеристики, полностью определяются эффективными площадями Sэ1(x), Sэ2(x) и внутренним объемом резино-кордной оболочки V.
Эффективные площади для верхнего и нижнего гофров пневматического упругого элемента с РКО тороидного типа определяются из соотношений
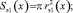
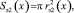
откуда
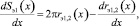
где rэ1,2(x) – эффективные радиусы верхнего и нижнего гофров пневмоэлемента с РКО тороидного типа.
Уравнения (1)–(6) позволяют выполнить расчет осевых нагрузочных характеристик пневматического упругого элемента с РКО тороидного типа для различных начальных значений избыточного давления и объема полости рабочего газа в РКО, если известны функции rэ1(x), rэ2(x).
В работе [5] исследовано влияние различных факторов: геометрии кордного каркаса, геометрических размеров и формы гофра оболочки на величину и характер изменения эффективного радиуса. При этом установлено, что в основном величина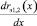 
зависит от углов наклона α(x) и β(x) нормалей, проведённых в точках сопряжения гофров оболочки с направляющими поверхностями ограничивающей металлоарматуры упругого элемента, которые определяются её конфигурацией и характеризуют степень её нелинейности.
Поэтому одной из основных задач выбора конструктивных параметров пневматических упругих элементов с РКО тороидного типа является расчет зависимости эффективных радиусов от осевого рабочего хода. Пневматические упругие элементы с РКО тороидного типа могут иметь различную конфигурацию направляющей арматуры, выбор которой определяется требованиями, предъявляемыми к пневмоэлементу, и в конечном счёте заданными нагрузочными характеристиками.
На рис. 1–3 представлены расчётные схемы для определения законов изменения эффективных радиусов пневматических упругих элементов с РКО тороидного типа для трёх различных форм линейных и сферических профилей направляющих поверхностей металлоарматуры.
В общем случае, определение законов изменения эффективных радиусов rэ1,2(x) пневматических упругих элементов с РКО тороидного типа для различных конфигураций направляющих поверхностей металлоарматуры сводится к решению системы геометрических соотношений, характеризующих произвольное положение упругого элемента, с учётом совместной работы верхнего и нижнего гофров:
ΣпрX = F1(x); ΣпрX = F2(x); l0 = const,
где l0 – длина профиля тороидной оболочки; τ – вектор, характеризующий геометрические параметры упругого элемента.
Для подавляющего большинства резино-кордных упругих элементов, в практике расчетов нагрузочных характеристик широко используется предположение о круговой форме гофра оболочки, кроме того, в последующих расчетах можно принять предположение о постоянстве длины профиля оболочки при перекатывании. Наряду с этим будем полагать резино-кордную стенку оболочки гибкой и тонкой, чтобы можно было пренебречь изгибающими моментами и поперечными силами в ней [8, 9, 11].
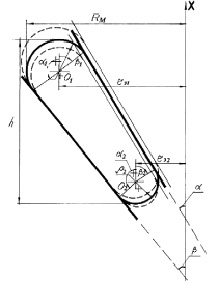
Рис. 1. Расчётная схема осевой нагрузочной характеристики пневмоэлемента с РКО тороидного типа
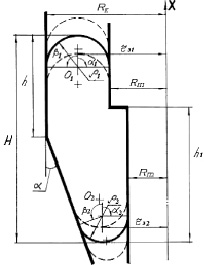
Рис. 2. Расчётная схема осевой нагрузочной характеристики пневмоэлемента с РКО тороидного типа
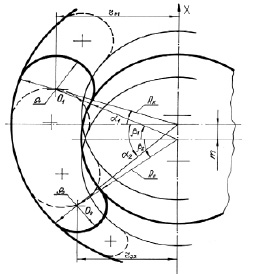
Рис. 3. Расчётная схема осевой нагрузочной характеристики пневматического упругого элемента с РКО тороидного типа
Принятые допущения значительно облегчают выбор геометрических параметров пневматического упругого элемента с РКО тороидного типа и позволяют оценить их влияние на характеристики пневмоэлемента.
Рассмотрим схемы пневматических упругих элементов с РКО тороидного типа, нагруженных осевой силой (нагрузкой) Q и внутренним (избыточным) давлением рабочего газа (рис. 1–3). Для определения геометрических параметров резино-кордной оболочки пневматического упругого элемента (эффективная площадь Sэ и внутренний объем V) необходимо рассмотреть осевую перекатку поршня относительно корпуса на величину хода X упругого элемента. Ход упругого элемента X определяется перемещением опорного элемента (поршня) относительно корпуса упругого элемента.
Для определения положения гофров РКО тороидного типа, при осевой деформации пневматического упругого элемента, имеющего конические поверхности направляющей арматуры (поршня и корпуса), была получена система уравнений следующего вида (рис. 1):
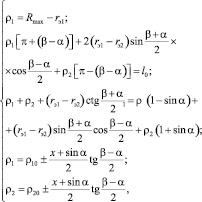
где ρ1, ρ2 – радиусы гофров РКО; α1 – угол наклона конической поверхности поршня упругого элемента; β1 – угол наклона поверхности корпуса упругого элемента; Rmax – максимальный радиус упругого элемента; l0 – длина профиля РКО.
Текущий объём РКО, в случае исполнения направляющих арматур в виде конических поверхностей (рис. 1), определяется с учётом (1) по следующим зависимостям:
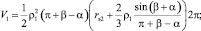
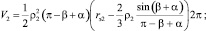
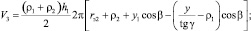
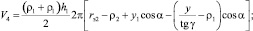
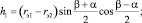
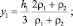
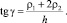
Система уравнений, описывающих профиль тороидной оболочки при осевой деформации пневматического упругого элемента, имеющего направляющие арматуры в виде конических и цилиндрических поверхностей (рис. 2), имеет следующий вид:
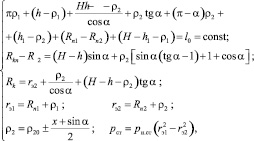
где Rn1 и Rn2 – радиусы поршня пневмоэлемента; α – угол наклона конической части корпуса упругого элемента; H – высота упругого элемента; Rл – радиус корпуса упругого элемента; ρ1 и, ρ2 и радиусы гофров PКO; ρ10 и ρ20 – радиусы гофров РКО в положении статического равновесия.
Уравнения для определения текущего значения объема РКО пневмоэлементов, имеющих поверхности направляющих арматур с такой конфигурацией (рис. 2), с учётом (3) имеют вид,
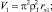
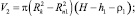
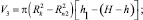
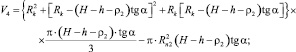
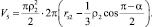
Расчетная схема для определения нагрузочной характеристики пневматического упругого элемента с РКО тороидного типа, у которого направляющая арматура (поршень и корпус) выполнены в виде двух сферических поверхностей, представлена на рис. 3.
Система геометрических соотношений, характеризующих произвольное положение РКО упругого элемента при его осевой деформации, определится из решения треугольников O1O2K, O1O2M, O1KM, O2KM и уравнения постоянства длины профиля оболочки:
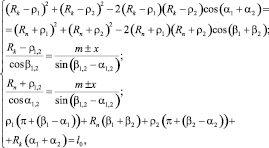
где l0 – длина профиля резино-кордной оболочки; ρ1 и ρ2 – радиусы гофров РКО; α1,2 и β1,2 – углы наклона нормалей, проведённых в точках сопряжения гофра оболочки с направляющими поверхностями ограничивающей арматуры (корпуса и поршня).
После решения приближёнными методами системы из шести нелинейных трансцендентных уравнений (2) можно получить текущие значения переменных β1, β2, α1, α2, ρ1, ρ2 в зависимости от величины хода x упругого элемента. Эффективные радиусы пневматического упругого элемента rэ1(x) и rэ1(x) определяются из соотношений
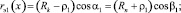
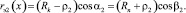
Значения текущего объёма, с учётом (1) определяются из соотношений
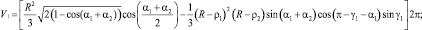
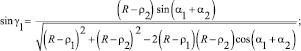
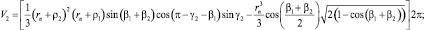
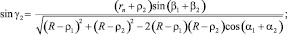
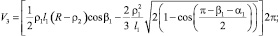
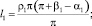
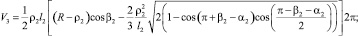
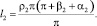
Таким образом, описанные закономерности изменения основных конструктивных параметров пневматического упругого элемента с РКО тороидного типа представляют собой математическую модель, позволяющую определять его осевые нагрузочные характеристики при различных соотношениях его геометрических параметров, которые определяют габариты и конфигурацию направляющих поверхностей металлоарматуры.