В машиностроительной практике находят применение так называемые механизмы перекатывающихся рычагов. Наиболее представительные сведения о строении и принципе действия таких механизмов приведены в справочнике [1] академика И.И. Артоболевского, где автором описаны пятнадцать их схем с одной высшей кинематической парой р4. Наличие двух подвижных кинематических пар является важной особенностью таких механизмов. Высшие пары позволяют в плоском механизме вращательное и поступательное относительные движения звеньев. Причем перекатывание одного рычага по другому может происходить как с проскальзыванием, так и без него.
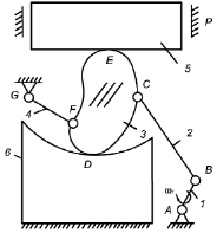
На рис. 1, a представлен механизм, перекатывающийся рычаг 3 которого входит в соединение с другими звеньями посредством двух высших кинематических пар (D и E). Механизм защищен патентом на изобретение [9].
a б
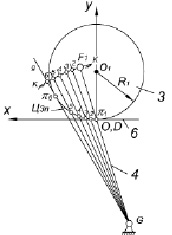
Рис. 1. К построению: a – механизма с перекатывающимся рычагом; б – центроид в абсолютном движении
Он приводится в движение от кривошипа 1, соединенного с шатуном 2 через вращательную кинематическую пару В. В свою очередь, шатун 2 входит во вращательную кинематическую пару С с перекатывающимся рычагом 3, который выполнен четырехпарным с двумя высшими кинематическими парами D и E и вращательной парой F коромысла 4. Перекатываясь со скольжением по неподвижному звену 6, рычаг 3 принуждает к поступательному движению ползун 5, воздействующий на обрабатываемый объект. Наличие трения скольжения в высших кинематических парах существенно уменьшает износостойкость звеньев и КПД механизма [6, 7]. В процессе износа падает точность воспроизведения необходимого закона движения выходного звена. Исключить трение скольжения можно путем подбора форм геометрических элементов звеньев [5], входящих в высшую пару. Согласно теореме Эйлера [8] «всякое непоступательное перемещение плоской фигуры в ее плоскости может быть осуществлено одним поворотом вокруг некоторого центра». При переходе к бесконечно близким положениям плоской фигуры, этот центр становится мгновенным центром вращения [4]. В литературе его также называют «полюсом» или «мгновенным полюсом» [10]. Так, движение плоского тела с точки зрения скоростей его точек может быть сведено к его вращению около мгновенного центра с некоторой мгновенной угловой скоростью. В процессе движения мгновенный центр перемещается от одной точки к другой как в движущемся теле, так и в неподвижном. Геометрическое место мгновенных центров в плоскости тела образует подвижную центроиду. При этом геометрическое место мгновенных центров на неподвижной плоскости образует неподвижную центроиду. Подвижная и неподвижная центроиды имеют в каждый момент общую точку (мгновенный центр вращения), то есть соприкасаются. Из равенства по величине скоростей мгновенного центра по центроидам вытекает равенство путей, проходимых им по подвижной и неподвижной центроидам за один и тот же промежуток времени, т.е. равенство элементарных дуг центроид между соответствующими друг другу смежными положениями мгновенного центра. Отсюда следует, что плоско-параллельное движение твердого тела (звена механизма) может быть воспроизведено качением без скольжения подвижной центроиды по неподвижной.
Если принять движение звена относительно неподвижного звена (стойки) за абсолютное, то соответствующий мгновенный центр будет назван мгновенным центром вращения в абсолютном движении рассматриваемого звена, а геометрическое место этих центров – центроидой в абсолютном движении [3]. В случае взаимодействия двух подвижных звеньев говорят о мгновенных центрах вращения в относительном движении. Эти центры образуют центроиды в относительном движении рассматриваемых звеньев. Таким образом, для обеспечения чистого качения необходимо, чтобы элементы звеньев, входящих в высшую кинематическую пару, представляли собой центроиды в абсолютном или относительном движении.
Поставим задачу спроектировать по представленной схеме (рис. 1, a) механизм, в высших парах (D и E) которого отсутствовало бы трение скольжения. При этом пара D должна представлять собой перекатывание центроид в абсолютном движении рычага 3, а пара E – взаимодействие центроид в относительном движении рычага 3 и ползуна 5.
Перейдем к построению центроид, основываясь на методах кинематической геометрии [2]. Начнем с построения центроидной пары D. Зададим декартову систему координат OXY (рис. 1, б), в которой построим перекатывающийся рычаг 3 с поверхностью в виде окружности радиуса R1 с центром O1. В качестве коромысла примем FG. Отметим траекторию точки F (рулетту КК), представляющую собой дугу окружности с центром G. Проведем из G касательную к окружности рычага 3 – луч Gg. Точку соприкасания обозначим π6. Полученный рабочий участок π1π6 на окружности образует подвижную центроиду Ц3п в абсолютном движении рычага 3. Разделим этот участок на интервалы. Полученные мгновенные центры вращения π1, π2, π3… соединим с G и продолжим лучи до пересечения с КК в точках F1, F2, F3… Далее строим неподвижную центроиду Ц3н – профиль стойки 6 (рис. 2). Мгновенные центры вращения, образующие неподвижную центроиду, договоримся обозначать P1, P2, P3… Для обеспечения чистого качения необходимо, чтобы соответствующие элементарные дуги центроид были равны, т.е. выполнялось условие
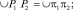
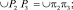
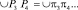 (1)
(1)
Для обеспечения зазора между центроидами должно выполняться следующее условие:
F2P2 = F1π2; F3P3 = F1π3; F4P4 = F1π4 ... (2)
Для этого из P1 проводим окружность радиуса π1π2. Из F2 проводим окружность радиуса F1π2, в точке пересечения окружностей отмечаем P2. Далее из P2 проводим окружность радиусом π2π3, а из F3 – окружность радиусом F1π3. На их пересечении отметим точку P3 и т.д. Соединив P1, P2, P3…, получим неподвижную центроиду Ц3н в абсолютном движении рычага 3. Таким образом, спроектированная высшая пара D будет обеспечивать перекатывание рычага 3 по стойке 6 без проскальзывания.
Переходим к рассмотрению вопроса о проектировании центроидной пары Е. Геометрический элемент перекатывающегося рычага 3 (центроиду в относительном движении Ц30 (рис. 3)) зададим в виде дуги окружности радиуса R2 с центром O2.
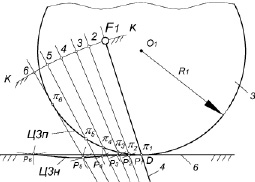
Рис. 2. Построение неподвижной центроиды
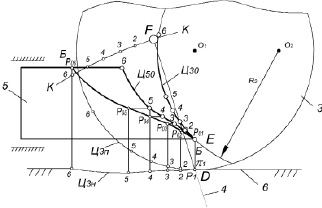
Риc. 3. Построение центроид в относительном движении
Так как центроиды должны перекатываться одна по другой без скольжения, то в точке соприкасания они должны иметь одинаковую линейную скорость, то есть
v5 = ω3PP0, (3)
где v5 – скорость ползуна 5; ω3 – угловая скорость рычага 3; Р – мгновенный центр вращения рычага 3 относительно стойки 6, а P0 – точка соприкасания рычага 3 с ползуном 5. Точки P01, P02, P03… лежат на прямых, перпендикулярных направлению поступательного движения ползуна 5. Направление движения ползуна примем горизонтальным. Для отыскания P01, P02, P03… проводим из мгновенных центров вращения P1, P2, P3… вертикальные линии. Далее, перекатывая без скольжения рычаг 3 по опоре 6, на пересечении центроиды Ц30 с вертикальными линиями отметим P01, P02, P03…. Точки пересечения отметим также на центроиде Ц30. Соединив P01, P02, P03… плавной линией, получим бицентроиду ББ – геометрическое место мгновенных центров вращения P0 в относительном движении двух звеньев, принадлежащее неподвижной плоскости. В P0 происходит соприкасание (зацепление) центроид, следовательно, бицентроида является линией зацепления центроид [3].
Из уравнения (3) следует
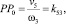
где k53 – передаточная функция между перекатывающимся рычагом 3 и ползуном 5. Таким образом, зная величины PP0 для каждого положения, можно построить график передаточной функции k53(φ3), представленный на рис. 4.
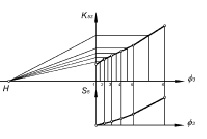
Рис. 4. Диаграммы передаточного отношения и перемещения
Переходим к построению центроиды Ц50 ползуна 5. Так как
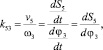
то есть
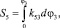
то перемещение ползуна 5 может быть определено путем графического интегрирования диаграммы k53(φ3) (рис. 4). При этом важно, чтобы масштаб диаграммы был согласован с масштабом чертежа. Из точек P0 бицентроиды (рис. 3) проводим линии, параллельные направлению движения ползуна. Откладываем на них значения перемещений S из диаграммы S5(φ3) и получаем точки, образующие центроиду в относительном движении Ц50. Таким образом, задав профиль центроиды Ц30 рычага 3 и построив профиль сопряженной центроиды Ц50 ползуна 5, мы обеспечили чистое качение в высшей кинематической паре E. Стоит отметить, что указанные построения являются приближенными. Степень точности кривых, очевидно, зависит от количества заданных точек и определяется исходя из технологического процесса, в котором участвует механизм.
Далее на перекатывающемся рычаге 3 отметим точку С. Найдем ее траекторию при перекатывании рычага в шестое положение. Зададим длину шатуна 2, после чего определим длину кривошипа АВ. Таким образом, спроектированный механизм имеет следующий вид, показанный на рис. 5.
Обратим внимание, что механизм собран в нескольких параллельных слоях. Так, кривошип 1 находится в первом слое, коромысло 4 – во втором, дуга окружности Ц3п рычага 3, перекатывающаяся по опоре 6 – в следующем слое, дуга окружности Ц30 рычага 3 и ползун 5 – в четвертом слое и шатун 2 расположен в пятом слое. Постоянное соприкосновение профилей звеньев высших пар достигается силовым замыканием, осуществляемым с помощью пружин.
Стоит отметить, что, исключив скольжение (поступательное движение) в высших кинематических парах D и E, эти пары остаются парами четвертого класса (двухподвижными). Так как при качении рычага 3 происходит поступательное движение центров кривизны центроид Ц3п и Ц30 – точек О1 и О2 (рис. 3).
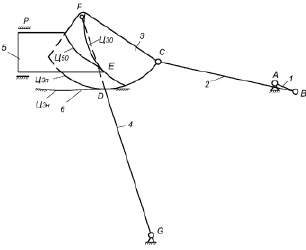
Рис. 5. Кинематическая схема спроектированного механизма
Проектируя указанный механизм, авторы задавались формой перекатывающегося рычага 3. При этом не ставили задачей отработку определенного закона движения ползуна 5. Однако с помощью изложенной в статье методики синтеза может быть воспроизведен необходимый закон движения выходного звена путем подбора профилей звеньев, входящих в высшие кинематические пары.



