Задача управления рисками является комплексной проблемой. Она включает в себя: выработку согласованного мнения об уровне приемлемого риска; оценку текущего состояния рисков от потенциально возможной реализации негативных событий (НС); синтез и реализацию мер по снижению уровня риска до заданных лицом, принимающим решения (ЛПР), значений. Вопросы, связанные с оценкой приемлемого и текущего риска неопределенностей, были рассмотрены в работах [2–3]. Возникающая при этом объективная неопределенность, источником которой являются природные или техногенные факторы, может быть формализована классическими методами теории вероятностей и математической статистики (ТВиМС) [4]. Для описания нечеткой информации субъективного характера целесообразно использование методов теории нечетких множеств и нечеткого когнитивного моделирования (НКМ). Их неоспоримыми достоинствами по сравнению с другими методами являются «возможность формализации численно неизмеримых факторов, использования неполной, нечеткой и даже противоречивой информации» [10].
В данной статье поставлена и решена задача синтеза управленческих решений по снижению рисков в нечетких условиях при ограниченных ресурсах.
Решение задачи
Числовые оценки рисков
Согласно общей схеме выбор стратегии управления уровнем рисков осуществляется на основе сравнения значений, описывающих текущее состояние системы, с приемлемыми для ЛПР значениями рисков [8]. Под приемлемым риском понимается такой риск, с которым ЛПР в данной ситуации может смириться [11]. В [2–3] было предложено приемлемый риск представлять в виде функциональной зависимости вероятности возникновения некоторого НС от величины возможного ущерба. Там же описана методика построения кривой приемлемого риска.
Для суммарной величины приемлемого риска Rпр получена формула
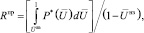(1)
где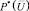 
– монотонно убывающая функция, отражающая приемлемую вероятность возникновения НС, приводящего к нормированному ущербу 
; 
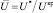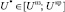; Uнз – ущерб, не являющийся значимым для ЛПР (т.е. такой, который может не приниматься им во внимание; 
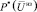может быть близка к «1»); 
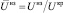– нормированное значение незначимого ущерба; Uкр – критический (максимально приемлемый для ЛПР) ущерб, вероятность возникновения которого необходимо свести к нулю:
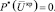
В качестве P* в [2–3] предложено использовать функцию вида
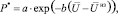(2)
где a и b – некоторые константы: a – соответствует вероятности, с которой ЛПР допускает возникновение не значимого для него нормированного ущерба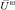 
; b – определяет скорость падения допустимой вероятности принятия ущерба по мере приближения к Uкр.
Для определения текущего уровня риска необходимо рассмотреть бизнес-процессы организации, выделить поддерживающие их активы. Затем выявить перечень возможных угроз, которым они могут быть подвергнуты. Далее для всех имеющихся активов необходимо оценить суммарный ущерб и вероятности его причинения со стороны всех возможных угроз с учетом предпринятых защитных мер.
Следует отметить, что одно НС может генерировать целую гамму точек, соответствующих определенным значениям ущерба и вероятности его возникновения. В результате получается множество точек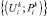 
, где i = 1...N; N – количество значений возможного ущерба; k = 1...K; K – количество НС. Если хотя бы одна из точек, описывающих текущее состояние риска, находится выше кривой приемлемого риска, необходимо принять меры по снижению рисков до приемлемых значений.
Стратегии снижения уровня риска
Риск-менеджмент предусматривает выбор одной из стратегий управления уровнем риска: сохранение риска (принятие текущего уровня риска – возможно с полным или частичным возложением ответственности за последствия реализации НС на третье лицо) или применение мер, нацеленных на снижение риска до заданных приемлемых значений [5; 8].
В свою очередь для реализации стратегии снижения риска возможно несколько тактических путей:
1) уклонение от угрозы или ликвидация источника угрозы;
2) снижение уровня уязвимостей за счет применения защитных мер;
3) снижение негативных последствий от реализации угроз.
Стратегии снижения рисков на рис. 1 соответствует перемещение точки, описывающей величину текущего риска, в зону приемлемого риска (ЗПР), которая находится под кривой приемлемого риска [3]. Выбор первых двух тактик предусматривает снижение вероятности возникновения НС, что соответствует смещению точки A0 (U0; P0) вниз по оси ординат (вариант 1 на рис. 1). Третий вариант направлен на снижение уровня ущерба от неблагоприятного воздействия: перемещение точки A0 влево по оси абсцисс (вариант 2 на рис. 1). Перечисленные тактики также могут комбинироваться с целью одновременного снижения вероятности возникновения НС и его последствий (вариант 3 на рис. 1).
При этом возникают следующие две основные задачи выбора оптимальной тактики снижения риска:
1) снижение риска при неограниченных ресурсах, выделенных для этого;
2) приведение величины риска в ЗПР при ограниченных ресурсах.
Рассмотрим пути решения сформулированных выше задач.
Введем следующие обозначения (см. рис. 2): Ai – точки, описывающие «текущий риск»;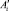 
(i = 1...n) – точки на кривой приемлемого риска, перемещение к которым от Ai будет оптимальным; 
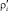– расстояние от точки Ai до точки 
; 
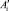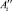– точки, соответствующие состоянию риска, которое достигается при недостаточном объеме ресурсов, выделенных на его снижение; 
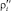– расстояние от точки Ai до точки 
.
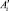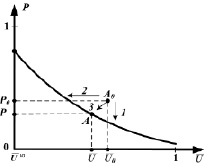
Рис. 1. Выбор тактики снижения риска
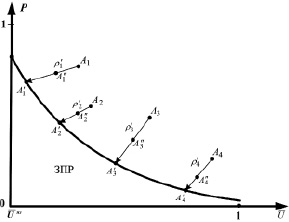
Рис. 2. Снижение риска при неограниченных и ограниченных ресурсах
«Стоимость» снижения условной единицы ущерба от реализации НС для i-й точки обозначим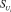 
, а «стоимость» снижения вероятности наступления НС для i-й точки – 
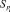. При этом в общем случае под «стоимостью» понимается совокупность дополнительных материальных, временных, человеческих и иных ресурсов, необходимых при реализации мер по снижению риска.
Для нахождения числовой характеристики «стоимости» снижения риска необходимо привести значения соответствующих ресурсов к безразмерной шкале от 0 до 1 (например, согласно шкале Харрингтона [12]), а затем найти аддитивную свертку вида
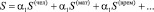(3)
где αi – «весовые» коэффициенты, определяющие «значимость» для ЛПР человеческих (S(чел)), материальных (S(мат)), временных (S(врем)) и других дополнительных ресурсов при осуществлении мер по снижению риска.
Часто при определении «весовых» коэффициентов в формуле (3) экспертам бывает затруднительно дать им четкие числовые оценки. В этом случае может быть использован предложенный в [1] метод нестрогого ранжирования, позволяющий находить искомые оценки в виде обобщенных весов Фишберна. Эффективность применения такого подхода основана на том, что «мягкие» качественные измерения типа сравнения, отнесения к классу, упорядочения гораздо более надёжны, чем назначение субъективных вероятностей, количественных оценок важности критериев, «весов» полезностей и т.п. [5, 9].
В [2] показано, что решение задачи 1 (снижение риска при неограниченных ресурсах) сводится к решению уравнения
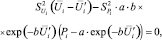(4)
где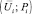 
– точка, характеризует текущий уровень риска; 
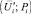– точка на кривой приемлемого риска; a, b – коэффициенты из формулы (2).
Решения данного уравнения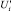 
могут быть найдены любым из известных численных методов [6] (например, методом хорд [7]).
Для вычисления значений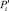 
необходимо подставить найденные значения 
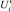в формулу (2). Отрезок, соединяющий точки (Ui; Pi) и 
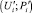, и будет искомой оптимальной траекторией снижения риска.
Для нахождения оптимальной траектории перемещения всей совокупности точек Ai необходимо минимизировать суммарную стоимость их перемещения в ЗПР:
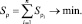(5)
При решении задачи 1 (при неограниченных ресурсах) нахождение минимума для Sρ сводится к нахождению минимума для каждого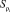 
согласно схеме, описанной в [2] и предусматривающей нахождение решения уравнения (4).
В случае с ограниченными ресурсами (задача 2) движение в ЗПР должно осуществляться по траектории, найденной при решении задачи 1 (поскольку она является оптимальной). Однако в общем случае точка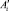 
при перемещении не достигается, поскольку сумма, выделенная на снижение риска 
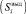, меньше суммы 
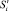, необходимой для достижения ЗПР. Перемещение заканчивается в точке 
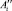. Исходя из этого, в случае ограниченных ресурсов задача поиска оптимальной тактики снижения рисков сводится к решению задачи линейного программирования:
(6)
где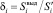 
– нормированное значение объема ресурсов, выделенных для снижения риска в i-й точке (δi ε [0; 1]); 
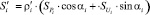– объем ресурсов, необходимый для достижения точкой Ai КПР; 
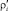– длина оптимальной траектории перемещения в ЗПР, полученная при решении задачи 1; αi = arctg(ΔUi/ΔPi); ΔUi и ΔPi определяются из решения задачи 1; Sвыд – объем выделенных ресурсов 
.
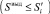Таким образом, для синтеза управленческих решений по снижению рисков может быть предложен следующий алгоритм:
1. Выделить основные бизнес-процессы, влияющие на эффективность работы организации, и определить активы, обеспечивающие их нормальное функционирование.
2. Вычислить величину приемлемого риска.
3. Оценить текущий уровень риска в организации.
4. Если хотя бы одна точка, описывающая текущее состояние, находится выше КПР, то решается задача 1: нахождение оптимальной траектории перемещения в зону приемлемого риска при неограниченных ресурсах. Рассчитывается суммарная «стоимость» затрат на снижение риска (сумма по всем опорным точкам) при перемещении по оптимальным траекториям Sρ.
5. Полученное значение сравнивается с величиной Sвыд, которую организация готова потратить на снижение рисков: ΔS = Sвыд – Sρ.
6. Если расчетная «стоимость» мер по снижению риска не выше выделяемой (ΔS ≥ 0), то мы имеем дело с задачей при неограниченных ресурсах, решение которой было найдено на шаге 4.
7. В противном случае решается задача 2 (при ограниченных ресурсах). По результатам вычислений ЛПР должно принять решение либо об увеличении величины приемлемого риска (до найденных значений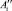 
), либо о выделении дополнительных ресурсов на осуществление мер по снижению уровня риска в размере ΔS.
Заключение
Таким образом, введение метрических характеристик для оценки приемлемого и текущего рисков, а также методик построения КПР и определения значений текущего риска позволило поставить и решить задачу выбора оптимальной тактики снижения текущего уровня рисков до заданного ЛПР приемлемого уровня при ограниченных ресурсах. Она учитывает наличие субъективной неопределенности при постановке задачи и оценке параметров, входящих в ее формализацию.