Простейшие методы анализа маркетинговых коммуникаций
С точки зрения маркетинговых коммуникаций целевым оптимизируемым показателем является конверсия. Конверсия понимается, как отношение числа участников маркетинговой коммуникации, выполнивших целевое действие, к их общему числу [7]:
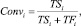
где Convi – конверсия в группе, обладающей i-м признаком; TSi – количество успешных попыток коммуникации по группе; TFi – количество безуспешных попыток коммуникации по группе.
Отображение значимости признаков с точки зрения конверсии можно представить графически с использованием системы простых показателей.
Количество клиентов, обладающих данным признаком, или их доля:
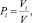
где Pi – доля клиентов, обладающих признаком i; Vi – количество клиентов, обладающих признаком i; V – общее количество клиентов в группе.
Распространённость признака в целевой группе – доля целевых клиентов, обладающих данным признаком:
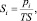
где Si – доля клиентов, обладающих признаком i, в целевой группе; pi – количество клиентов в целевой группе, обладающих признаком i; TS – количество клиентов в целевой группе (успешных попыток коммуникации).
Таким образом, можно вывести коэффициент характерности признака, показывающий, насколько этот признак более или менее характерен для целевого клиента, чем для группы в целом:
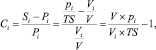
где Сi – коэффициент характерности признака i для целевой группы, показывает ценность обладания информацией о факте присутствия признака i.
По результатам проведения маркетинговой кампании был составлен портрет потенциального лизингополучателя, который был описан при помощи полученных выше метрик (рис. 1).
Помимо основных признаков были выявлены синтетические признаки, состоящие из совокупности условий (рис. 2).
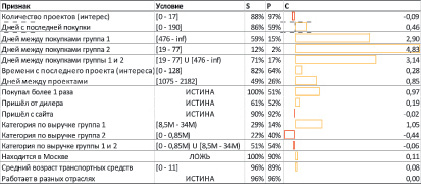
Рис. 1. Анализ основных характеристик клиента
Рис. 2. Анализ синтетических характеристик клиента
Таким образом, самая ценная информация о клиенте с точки зрения отклика на маркетинговые коммуникации звучит следующим образом «клиент совершает покупки в среднем раз в 19–77 дней», однако таких клиентов всего 2 %.
Информация о том, что выручка клиента составляет менее 850 000 рублей, говорит о том, что, скорее всего, клиент не склонен к покупке, причём данная информация имеется о 40 % респондентов, что является относительно хорошим показателем.
Итоговый портрет целевого клиента будет звучать следующим образом «клиент часто совершает покупки, недавно что-либо покупал или интересовался покупкой, пришёл от дилера и имеет выручку от 8,5 до 34 млн руб.». Очевидно, что таких клиентов либо крайне мало, либо не существует вовсе. Однако такой портрет позволяет дать ориентиры в стратегическом планировании и при подготовке очередных маркетинговых кампаний.
Использование нелинейных методов отображения данных в анализе маркетинговых коммуникаций
Целесообразно рассмотреть методы, которые в настоящее время позволяют визуально представить сразу всю структуру многомерного набора данных.
Под визуализацией данных в таком случае будет пониматься способ отображения многомерного массива данных на двумерной плоскости, где по меньшей мере качественно выражены основные закономерности исходного распределения. Это могут быть такие закономерности, как кластерная структура, топология, различные зависимости между признаками, расположение точек данных в пространстве и пр. [5].
Основные цели применения нелинейных методов визуализации:
– наглядное геометрическое представление данных;
– описание закономерностей в данных;
– сжатие информации;
– восстановление пропущенных значений;
– прогнозирование и построение регрессионных моделей.
Традиционными методами решения поставленных задач являются целенаправленное проецирование и многомерное шкалирование. Методы целенаправленного проецирования сводятся к поиску отображения данных из многомерного пространства на двумерную плоскость, оптимизирующему функционал от координат точек данных [1]. В задачах, решаемых методами многомерного шкалирования, отсутствуют исходные данные о координатах точек данных, известны только расстояния между ними. Задача сводится к поиску таких координат точек, которые будут сохранять матрицу расстояний [2, 4, 8].
Относительно новыми средствами визуализации данных являются самоорганизующиеся карты Кохонена [9], а также упругие карты, разработанные в Институте вычислительного моделирования г. Красноярска [6]. Методы, используемые этими средствами, основаны на поиске оптимальной ориентации вложенных поверхностей в многомерной структуре данных.
В методе самоорганизующихся карт Кохонена точки данных проецируются на сетку узлов, итеративно приближенных к сгущениям точек данных, при достижении минимума ошибки аппроксимации:
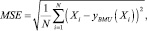
где yBMU(Xi) – ближайший узел к точке данных Xi.
Узлы сетки инициализируются и перемещаются по направлению к точкам данных по следующему правилу:
(yj)′ = yj + h(r(yj, yBMU), t)(Xi – yi), j = 1…p,
где h(x, t) – функция соседства узлов; r(y1, y2) – расстояние между узлами сетки y1 и y2; p – количество узлов сетки.
Ниже описаны часто используемые функции соседства:
Гауссова функция
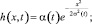
Bubble-функция:
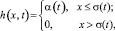
где α(t) – так называемый темп обучения; σ(t) – радиус захвата соседей [5].
Для анализа данных выполним нормализацию по формуле
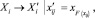
где n – объём данных, xi1, …, xin – набор уникальных значений признака Xi; 
– набор уникальных значений признака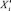 
; F(xij) – эмпирическая функция распределения признака Xi:
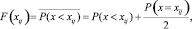
где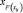 
– есть квантиль уровня F(xij) для нормального распределения
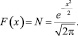
Построим карту Кохонена, по очереди отбрасывая неинформативные признаки с точки зрения конверсии (рис. 3).
Самыми информативными оказались следующие признаки: «Имеет проект, заведённый по собственной инициативе» (характерно для группы с высокой конверсией), «Дней между передачами» (низкие значения характерны для группы с низкой конверсией), «Интересовался ли разными транспортными средствами» (не характерно для группы с низкой конверсией), «Пришёл от дилера» (не характерно для группы с высокой конверсией), «Имеет упрощённую систему налогообложения» (весьма характерно для группы с низкой конверсией), «Дней прошло с последней покупки» (высокие значения не характерны для группы с низкой конверсией).
Конкретные диапазоны, соответствующие нормированным значениям, можно вывести обратным преобразованием признаков.
Метод упругих карт может служить обобщением метода главных компонент. Задача построения вложенного многообразия является оптимизационной и состоит в поиске такой нелинейной (упругой) поверхности, дисперсия проекций точек данных на которую будет минимально искажена по сравнению с дисперсией исходных точек данных. Изначально упругая сетка может располагаться в плоскости первых двух главных компонент.
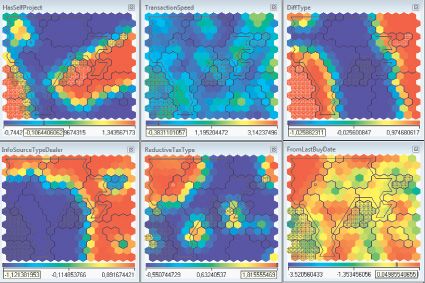
Рис. 3. Карта Кохонена: Закрашенная область – кластеры с высокой конверсией (2, 3, 4), обведённая контуром область – кластеры с низкой конверсией (0, 1, 6, 7, 9)
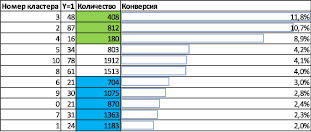
Рис. 4. Статистика по кластерам
Рис. 5. Статистика по группам кластеров
Для метода главных компонент задача формально ставится следующим образом
Старые признаки должны как можно точнее линейно восстанавливаться по новым:
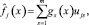= 1, …, n, ∀x ∈ X
как можно точнее на обучающей выборке x1, …, xl:
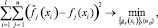
где f1(x), …, fn(x) – исходные числовые признаки; g1(x), …, gm(x) – новые числовые признаки, m ≤ n.
Исходная матрица «объекты-признаки»
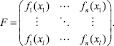
Новая матрица «объекты-признаки»
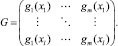
Матрица линейного преобразования признаков:
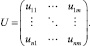
Матричная запись линейного преобразования
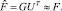
Матричная запись оптимизируемого функционала
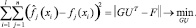
Решением задачи метода главных компонент является нахождение матрицы U. Столбцы U – это собственные векторы матрицы FTF, соответствующие максимальным собственным значениям λ1, …, λm [3].
G = FU.
Упругая сетка имеет узлы, нумеруемые индексами yij, i = 1…p, j = 1…q. Каждый узел yij ставится в соответствие подмножеству точек данных Kij (i = 1…p, j = 1…q) так, что этот узел для каждой точки из этого подмножества является ближайшим:
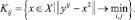
Конечное положение упругой сетки достигается оптимизацией линейной комбинации функционалов, отражающих следующий набор свойств:
1. Близость к точкам данных:
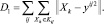
2. Упругость по отношению к растяжению:
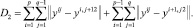
3. Упругость по отношению к изгибу:
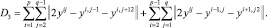
Таким образом:
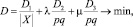
где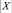 
– число точек данных; λ, μ – коэффициенты «упругости» сетки.
Построим двумерную упругую карту с параметрами λ = 0,01, μ = 2 и развернём на плоскости (рис. 6).
Рис. 6. Упругая карта. Распределение плотности данных. Белым отмечены точки данных, соответствующие успешным коммуникациям
Рис. 7. Упругая карта. Дано 6 раскрасок в разрезе информативных признаков: 1 – «Интересовался разными ТС»; 2 – «Прошло дней с последней покупки»; 3 – «Имеет самостоятельно заведённый проект»; 4 – «Имеет упрощённую систему налогообложения; 5 – «Пришёл от дилера»; 6 – «Частота покупок»
Отразим данные на карте в разрезе информативных признаков, аналогично карте Кохонена (рис. 7).
Выполним кластеризацию методом k-means с пятью кластерами (рис. 8) и составим статистику (рис. 9).
Рис. 8. Кластеризация после построения упругой карты
Рис. 9. Статистика кластеров после применения упругой карты
Кластером с наиболее высокой конверсией (8,26 %) оказался кластер № 1, содержащий 16,33 % испытаний, для которого характерны признаки: «Скорее интересуется разными ТС», «Имеет недавнюю покупку», «Имеет проект, заведённый по собственной инициативе».
Кластером с наиболее низкой конверсией (0,89 %) оказался кластер № 3, содержащий 39,31 % испытаний, для которого характерны признаки: «Скорее не интересовался разными ТС», «Не имеет недавнюю покупку», «Не имеет проект, заведённый по собственной инициативе», «Имеет низкую частоту покупок»
Заключение
Применение упругих карт позволило сделать лучшую кластеризацию, по сравнению с картами Кохонена: гораздо лучше были классифицированы клиенты с очень низкой конверсией и сравнительно неплохо были классифицированы клиенты с высокой конверсией. Были получены наглядные результаты в виде плотности распределения данных, распределения значимых признаков, а также распределения кластеров. Полученные данные могут быть применены при построении регрессионных решений и планировании маркетинговых коммуникаций.