Ряд результатов по теме данной работы представлены в [2, 4, 5, 6]. Программная реализация ряда алгоритмов по оценке качества поверхности материалов, полученных методом прямого сканирования, приводится в [3, 7, 8, 9].
В ранних программах авторов использовался MATLAB. В [3, 7, 9] применяется компилируемый язык программирования C# на платформе .NET, где существует богатая библиотека классов по обработке изображений цветовых моделей RGB. Здесь рассмотрим более подробно некоторые методы и алгоритмы по оценке качества поверхностей изделий и конструкций.
В силу выбранной цветовой модели RGB предлагается отдельное рассмотрение распределения яркости пикселей по каждой составляющей RGB, т.е. по матрицам красного, зеленого и синего цветов. Предполагается, что распределение яркости пикселей в общем случае носит произвольный характер. Поэтому можно использовать различные статистические методы и приемы для расчета характеристик, в частности, среднего арифметического, исправленной выборочной дисперсии, стандартного отклонения, множественного коэффициента корреляции, нормированной автокорреляционной функции [3]. В [9] введены такие показатели, характеризующие изображение образца, как тоновая контрастность, тоновая насыщенность, среднее абсолютное отклонение (MAD – Mean Absolute Deviation) разницы кодов RGB сравниваемых изображений. В программах [7, 9] введены такие показатели качества изображений, как треугольники яркости, треугольники стандартных отклонений яркости, относительные коэффициенты соответствия, изменяющиеся от нуля до единицы.
Среднее арифметическое значение распределения яркости пикселей изображения может быть вычислено как среднее по всем компонентам модели RGB. Но в работах [2, 4, 5, 6] приводится расчет среднего арифметического значения яркости изображения по составляющим RGB – по матрице красного, матрице зеленого и матрице синего цветов. При этом обход матриц осуществляется по высоте и по ширине отсканированного образца какого-либо материала. Это означает, что будет получен одномерный массив данных о яркости пикселей соответствующего цвета, каждая точка которого есть среднее арифметическое по высоте или по ширине изображения. В итоге можно построить кривую в декартовой системе координат, ось абсцисс которой есть размер либо высоты, либо ширины изображения, а ось ординат – это яркость кода RGB в пределах от 0 до 255. Аналогичным путем вычисляется массив исправленной выборочной дисперсии как меры отклонения от среднего. Пример изменения средних значений кода RGB конкретного материала (рис. 1, а) приведен на рис. 1, б и в. Как видно из рис. 1, коды RGB по высоте образца заметно отличаются от кодов RGB по ширине, что означает неоднородность поверхности материала исследуемого образца.

а
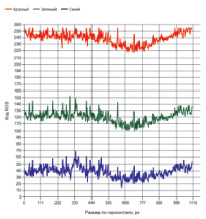
б в
Рис. 1. Изменение средних значений кода RGB: а – изображение исследуемого образца (размер 1104×1635 px); б – изменение средней яркости по ширине образца; в – изменение средней яркости по высоте образца
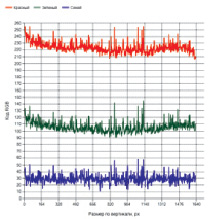
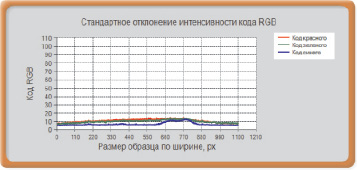
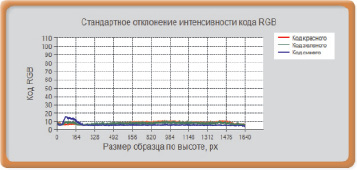
По аналогии можно найти массив значений стандартного отклонения (среднее квадратическое отклонение) по высоте и ширине образца. Стандартное отклонение – это плюс корень квадратный из дисперсии. Для неслучайных величин стандартное отклонение равно нулю. Поэтому чем больше величина стандартного отклонения, тем менее однороден образец материала, и наоборот. По характеру изменения стандартного отклонения также можно определить неравномерность окраски образца.
Примеры изменения стандартных отклонений приведены на рис. 2.
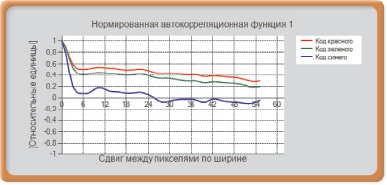
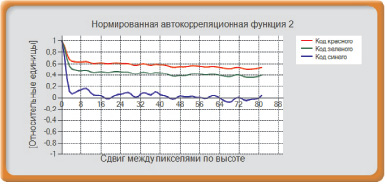
Как известно, нормированная автокорреляционная функция характеризует статистическую связь между данными. При отсутствии такой связи функция стремится к нулю. Для определения корреляционной функции по результатам опыта выбирается достаточно большой объем выборки, чтобы можно было в широком диапазоне формировать разницу между двумя соседними значениями случайных чисел. Эту разницу для непрерывного времени обычно обозначают τ, а корреляционную функцию – R(τ). Если объем выборки составляет N, то диапазон вычисления корреляционной функции будет определяться как N – τ. Величина τ задает область определения корреляционной функции. Например, τ может меняться от 0 до 6–8. При этом N должно быть много больше 6 или 8. Область суммирования принимает значения от 1 (первое случайное число выборки) до N – τ. Корреляционная функция вычисляется по следующей экспериментальной формуле [1]:
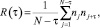
где nj – случайное число из заданной выборки случайных чисел размера N.
Нормированная корреляционная (и автокорреляционная) функция получается из корреляционной функции, деленной на дисперсию данной выборки.
а
б
Рис. 2. Изменение стандартного отклонения по ширине (а) и высоте (б) образца
а
б
Рис. 3. Изменение автокорреляционной функции по ширине (а) и высоте (б) образца
Примеры нормированных автокорреляционных функций для образца, представленного на рис. 1, показаны на рис. 3.
Анализ образца (см. рис. 1, а) выполнен на основе разработанной программы авторов [3]. Расчет среднего арифметического одномерного массива соответствующей компоненты кода RGB не представляет особых затруднений. Расчет стандартного отклонения выполняется на основе расчета исправленной выборочной дисперсии (D) по формуле
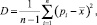
где n – размер массива; pi – средняя яркость точки (пикселя);  – среднее арифметическое яркости пикселей (по высоте или по ширине).
– среднее арифметическое яркости пикселей (по высоте или по ширине).
Для оптимизации вычисления дисперсии обычно рассчитываются первый m1 и второй m2 начальные моменты за один проход массива данных, после чего исправленная выборочная дисперсия рассчитывается по формуле
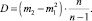
В [7, 9] предусмотрен анализ каждого из компонентов кода RGB. Подход к анализу аналогичен предыдущим случаям.







а б в г д е ж
Рис. 4. Поверхность образца до (а) и после (б–ж) воздействия агрессивной среды
а
б
в
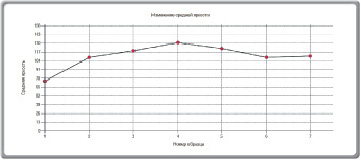
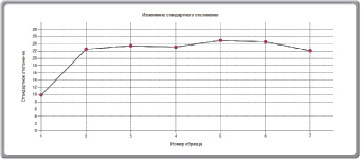
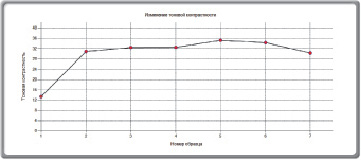
Рис. 5. Изменение средней яркости (а), стандартного отклонения (б) и тоновой контрастности образцов в результате агрессивного воздействия

а
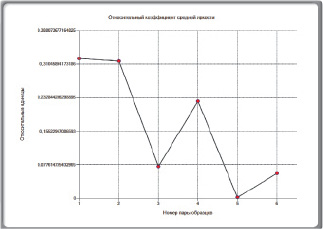
б
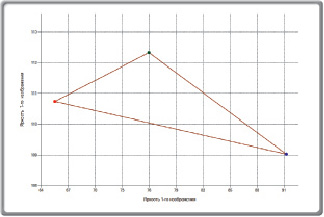
в
Рис. 6. Изменение тоновой насыщенности (а) и относительного коэффициента яркости (б) образцов в результате агрессивного воздействия неблагоприятных факторов. Треугольник яркости двух сравниваемых образцов (в)
В качестве числовой оценки изменения свойств материала, подвергавшегося внешним неблагоприятным факторам, предлагается ввести относительный коэффициент соответствия. Он изменяется от нуля до единицы. Единица соответствует полному совпадению сравниваемых образцов. Чем ближе к нулю, тем больше различий между образцами. Алгоритм вычисления относительного коэффициента соответствия заключается в определении треугольников яркостей образцов, вершины которых соответствуют средним значениям (или стандартным отклонениям) кодов красного, зеленого, синего. Затем вычисляются площади треугольников. И, наконец, берется отношение меньшей площади к большей. Очевидно, что если площади одинаковые, то относительный коэффициент соответствия будет равен единице.
Рассмотрим пример сравнения образцов относительно контрольного образца. Другие образцы – это результат воздействия неблагоприятных факторов в течение 6 месяцев (10 % раствор серной кислоты). На рис. 4 приведен контрольный образец и часть остальных образцов. Изображения поверхности образцов, приведенные на рис. 4, получены методом прямого сканирования с помощью сканера типа HPScanJet 2400.
Результаты анализа отсканированных изображений с помощью разработанного программного комплекса [9] можно вывести в виде графиков изменения средней яркости образцов, стандартного отклонения, тоновой контрастности и насыщенности, относительного коэффициента и треугольника яркости. На рис. 6, 7 представлены результаты анализа поверхности образцов, подвергшихся неблагоприятным факторам в течение шести месяцев.
Согласно данным (рис. 5, 6) значительное изменение цвета поверхности наблюдается уже после первого месяца воздействия агрессивной среды (обнаруживается большая неоднородность окрашивания материала, появление светлых пятен). На рис. 6 в показан треугольник яркости двух изображений – первого (контрольного) и последнего. Идентичные изображения будут иметь одинаковые треугольники яркости. Вершины треугольника представляют собой средние значения матриц компонент RGB, вычисленные по высоте и ширине образца. В частности, для контрольного образца (1-го изображения) и последнего (7-го изображения) образца получены следующие значения площадей (в квадратных единицах – кв. ед.) треугольников яркости и относительный коэффициент соответствия:
1) площадь треугольника средней яркости 1-го изображения 17,52526 кв. ед.;
2) площадь треугольника средней яркости 7-го изображения 1,00639 кв. ед.;
3) относительный коэффициент соответствия площадей яркости двух изображений равен 0,057425.
Введенный относительный коэффициент соответствия дает числовую оценку несоответствия изображений, которую затруднительно определить визуально. Соответственно, приведенные диаграммы в программе [9] сопровождаются числовыми результатами. Поэтому сравнительный анализ образцов можно осуществлять не только визуально по графикам, но и при сравнении числовых показателей. В программе предусмотрено сравнение всех образцов относительно контрольного образца – изображения.
Разработанная методика оценки декоративных свойств покрытий позволяет моделировать изменение цвета и качества поверхности различных строительных материалов, изделий и конструкций под воздействием эксплуатационных факторов. Рассмотренные зависимости дают визуальную картину изменения свойств материалов в течение времени, а также числовые характеристики этих зависимостей.



