Известно, что в гидравлических цепях волновой процесс формируется противодействием нескольких процессов: сжатия флюидов/скелета, вязкостным трением и силами инерции (второй закон Ньютона).
Несмотря на достаточную изученность данных процессов в отдельности, к сожалению, при моделировании процессов фильтрации в поровых и трещинопоровых средах они в комплексе не нашли отражение в общей системе уравнений, решаемой в классических (принятых в качестве основных при проектировании разработки месторождений углеводородов) симуляторах – Эклипс, Темпест, Техсхема и т.п. Более того, вычислительная схема (полностью или частично неявная) не позволяет прогнозировать негармонические колебания, вызванные историей гидродинамического воздействия на продуктивные пласты и любые гидравлические цепи в принципе.
Вследствие чего прогнозирование волновых процессов в поровой и трещиноватой среде крайне важно в текущих тенденциях.
Авторами данной статьи разработан и используется вычислительный программный комплекс (ВПК) Немезида [4] (с. Гидрасим) (рис. 1), апробированный множеством научных работ и подтвержденный многочисленными промысловыми и лабораторными экспериментами [3, 5].
В частности, в 2008 г. была создана стендовая установка для испытания разветвленной гидросистемы в условиях нестационарных волновых процессов и в т.ч. гидроударов. Результаты стендовых испытаний подтверждают корректность разработанной модели [5] посредством сопоставления результатов вычислительных экспериментов на ВПК и физической модели (стендовой установки).
Задачи ВПК охватывают прогнозирование гидродинамических показателей в наземных трубопроводных сетях, скважинах, пластах, трещинах и внутрипоровом пространстве на основе обобщения законов сохранения массы, энергии и законов вязкостного трения в любых по природе средах. Модель, заложенная в основу программного комплекса, является полностью нелинейной, нестационарной и неизотермической, учитывающей закон инерции и, как следствие, волновые процессы. Это позволяет расширить спектр задач, объединяющий тепловые, гидромеханические, химические и механические процессы.
Вследствие наибольшей универсальности разработанная модель ВПК позволяет прогнозировать как гармонические, так и негармонические колебания, являющиеся естественными или следствием работы элементов управления, параметрами энергообмена и физическими свойствами текучих сред (рис. 2). Математический аппарат в отношении волновых процессов описан в работе [5].
Особенно важно отметить, что при условии существования в продуктивных коллекторах сети трещин требуется особое внимание уделять технологии гидродинамического воздействия на пласты, так как структурная неоднородность сети каналов со сверхпроводимостью является решающим фактором при планировании мероприятий по повышению эффективности извлечения углеводородов.
Последние исследования авторов, как наследие более старых исследований [3], направлены на изучение нестационарных процессов в техногенных и природных гидравлических системах.
В ходе стендовых испытаний [3] в 2008 г. было обнаружено «странное свойство» некоторых гидравлических систем: при определенных условиях запуска гидросистема не выходит на стационарный режим.
Вместе с тем известно, что любая система стремится перейти от неравновесного состояния к равновесному, т.е. стационарному или квазистационарному состоянию, в котором во всех узлах системы устанавливаются определенные давления, а в участках системы определенные расходы. На этом принципе, например, основан часто применяемый метод исследования скважин – снятие и обработка «индикаторных линий и диаграмм». На данном же принципе основаны методы решения задачи потокораспределения [2].
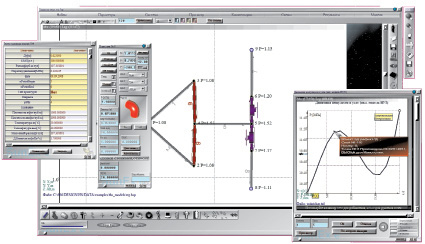
Рис. 1. Моделирование волновых процессов в вычислительной стендовой установке в ВПК «Немезида»
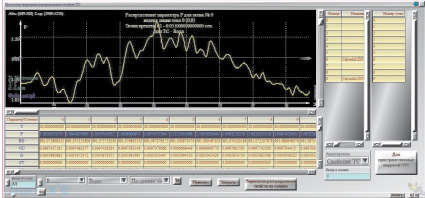
Рис. 2. Демонстрация волнового процесса в системе трещин продуктивного пласта ВПК «Немезида»
В результате ряда вычислительных и подтверждающих их лабораторных экспериментов (на стендовой установке) установлен крайней важный и нетривиальный факт: в зависимости от структуры системы, параметров ее элементов, начальных условий и условий на ее границах гидравлическая система может не выходить на комплексный стационарный режим, характеризующийся условно постоянными давлениями и скоростями потоков в элементах системы.
Очевидно, данный вывод должен противоречить обобщению теоремы Максвелла о принципе наименьшего теплового действия на гидравлические цепи. Однако на основе последнего принципа построить вычислительную схему для решения задачи потокораспределения так и не удалось.
Из такой ситуации гипотетически можно было бы предположить невозможное: нарушение закона сохранения энергии. Однако, разумеется, это не так.
Основным признаком такого – особого состояния гидросистемы, когда она не выходит на стационарный режим, является сохранение автоколебаний давления и скоростей в некоторых участках системы со сдвигом фаз и разными амплитудами. Иными словами, когда в одном из участков наблюдается снижение скорости течения и снижение диссипации гидравлической энергии в тепловую, при этом в другом элементе прослеживается рост скорости и перепада давления на вязкостное трение.
Таким образом, система находится на таком же энергетическом уровне, как и идеально вышедшая на стационарный режим, хотя в отдельных узлах и участках структуры происходят незатухающие колебания с амплитудой до 0,5–5 МПа.
Так как для вычислительных экспериментов использовалась полностью явная схема вычисления с шагом 1 мкс и при этом соблюдалась гладкость решения, то можно прийти к обоснованному теоретическому выводу о том, что данные автоколебания не являются результатом неточностей вычислительного эксперимента и результатом ошибок лабораторного эксперимента [3].
Экспериментально также установлено, что одна и та же гидросистема с различных начальных распределений давления переходит в различное условно стационарное состояние (рис. 3, б и в). То есть уровень энергии одинаков, при этом характеристики автоколебаний могут отличаться.
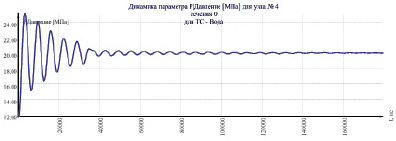
а
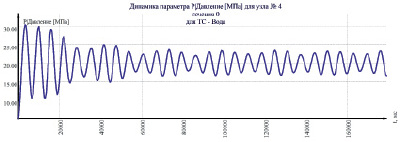
б
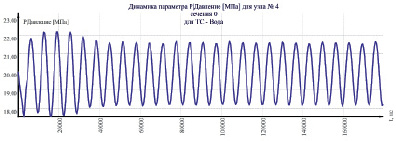
в
Рис. 3. Динамика давления узла 4 с различных начальных давлений: а – 11 МПа; б – 5 МПа; в – 20 МПа
Следует отметить, что, рассчитывая любые гидравлические системы, будь то наземные сети с развитой структурой или продуктивные пласты с изотропной структурой или трещиноватой структурой, и предполагая оптимальным и технологически номинальным (или даже возможным) состоянием системы исключительно стационарный режим (как на рис. 3, а), мы находимся в заблуждении. Иначе говоря, волновые процессы в природе гидросистем – есть одно из средств сохранения их состояния с наименьшим уровнем диссипации энергии.
Данный вывод тесно связан и с пониманием стационарного состояния в квантовой физике.
Колебательный волновой процесс формируется так, что потенциальная величина давления стационарного состояния находится ровно между максимумом и минимумом давления с периодическим профилем волны, как при субгармонических (рис. 3, в), так и не гармонических (рис. 3, б) колебаниях.
В таких неклассических условиях «квазистационарных процессов» материальный баланс в узловых соединениях не соблюдается (рис. 4), из-за чего и меняется давление вследствие сжимаемости среды.
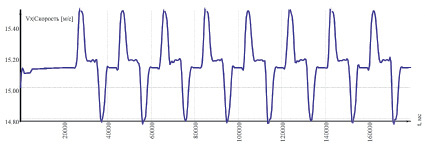
Рис. 4. Динамика скорости в одном из участков гидросистемы для случая запуска с давления 5 МПа
Как уже отмечалось [4], волновые процессы в продуктивных коллекторах с развитой сетью трещин (рис. 2) требуют дальнейшего изучения и технологического использования с целью повышения нефтеотдачи пластов с низкой поровой проницаемостью.
Дальнейшим развитием понимания волнового энергообмена в пластовых и наземных гидросистемах является оценка волновых процессов в многофазных взаиморастворимых средах. При этом свойства жидкостей и газов, вносимых в ПВК, должны непосредственно описываться PVT-функциями и системой взаимодействия макрокомпонентов. Последнее позволяет учитывать взаимное трение и переходные массообменные процессы фаз и компонентов, заменяя уравнения состояния в наиболее универсальной постановке.



