Снижение материалоемкости конструкций при сохранении прочности и надежности является важной задачей. В современном строительстве объектов нефтегазового комплекса широко и многофункционально используются многослойные пластины. Применение таких конструкций обусловлено их высокой прочностью и жесткостью при относительно малой массе, хорошими тепло- и звукоизоляционными свойствами. Слои пластин выполняют как из новых, так из традиционных материалов. Эти материалы характеризуются свойством разносопротивляемости в той или иной степени, то есть имеют различные модули упругости при растяжении и сжатии. Решение задачи напряженно-деформированного состояния многослойных пластин из разномодульных материалов с учетом жесткости межслойных связей является актуальной проблемой.
Цель исследования: получить формулы для определения интегральных характеристик жесткости i-го слоя составной многослойной пластины с учётом разномодульных свойств материала.
Материалы и методы исследования: в работе использовались теоретические и экспериментальные методы исследования, основанные на математическом моделировании.
Результаты исследований и их обсуждение
Теория изгиба рассматривается для составных многослойных пластин с учётом разномодульных свойств материалов слоев. Как и в [7], под составной пластиной понимаем две и более пластины. Каждую отдельную пластину рассматриваем как i-й слой, количество которых равно n + 1. Число промежутков между ними (швов) равно n. Нумерацию устанавливаем сверху. Слои в составной конструкции соединены между собой упругоподатливыми связями, допускающими сдвиг одного слоя по отношению к другому. Поперечные связи абсолютно жесткие. В соответствии с этим все слои имеют одинаковый прогиб W(x, y). Гипотеза Кирхгофа – Лява выполняется для отдельного слоя, но не для пакета в целом. Нагрузка на пакет направлена по нормали и распределяется на поверхности по произвольному закону. Решение задачи определения напряженно-деформированного состояния таких конструкций проводится с учетом жесткости межслойных связей и разномодульных свойств отдельных слоев.
В разномодульной теории упругости определяющим является знак главного напряжения [2, 3]. Точки или области тела, где все главные напряжения имеют одинаковые знаки (т.е. тело сжимается или растягивается по главным напряжениям), будем называть точками или областями первого рода и на них в данной работе останавливаться не будем. Те точки или области тела, где одно из главных напряжений имеет отличный от двух других знак, будем называть точками или областями второго рода. Физические соотношения, определяющие зависимость деформирования материала от величины напряжений, запишем только для области второго рода. Разномодульность связана с положением главных площадок [1].
В координатах, определяющих положение главных площадок, для плоского напряженного состояния матрица податливостей запишется в виде
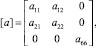(1)
где элементы aik зависят от напряженного состояния, например если σ1 > 0, σ2 < 0, то a11 = 1/E+; a22 = 1/E–;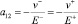 
(E+, E– – модули упругости при растяжении и сжатии соответственно).
В данной работе переход от направлений главных площадок к координатам X, Y осуществляется через преобразование матрицы податливостей [4]. Это позволит записать интегральные характеристики жесткости, а следовательно, систему дифференциальных уравнений в координатах X, Y. Считаем, что оси координат совпадают со сторонами пластины.
В отличие от существующих моделей [6], чтобы перейти от координат главных площадок к матрице жесткостей в декартовых координатах, необходимо иметь полный набор характеристик жесткостей в главных координатах. В то же время при s1 > 0, s2 < 0 на двух ортогональных площадках имеем характеристики материала, соответствующие растяжению и сжатию, поэтому следует различать податливости на сдвиг 1/G+ и 1/G–.
Результирующая величина податливости на сдвиг a66 определялась путем осреднения величин, которые имелись в одной точке на двух площадках, ортогональных X, Y:
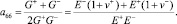(2)
От матрицы податливости aik (1) в координатах главных площадок перейдем к матрице Aik в координатах X, Y:
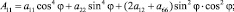
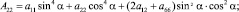
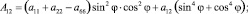
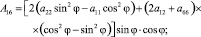(3)
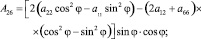
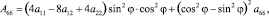
где φ – угол, определяющий положение главных площадок по отношению к координатам X, Y.
Соотношения между напряжениями и деформациями в координатах X, Y с учетом новой матрицы (3) запишутся как
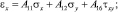
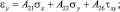
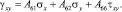(4)
Напряжения через компоненты деформаций запишем в форме [3]
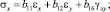
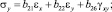
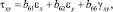(5)
где
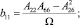
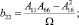
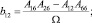
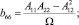(6)
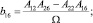
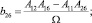
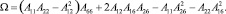
Соотношения сводятся к (1), если направления главных площадок совпадают с координатами X, Y.
Запишем выражения для напряжений в слое, с учетом распределения по толщине i-го слоя, в рамках гипотезы прямых нормалей:
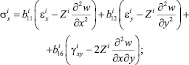
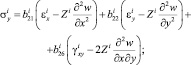(7)
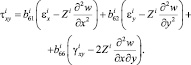
Здесь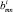 
– характеристики жесткости в точке материала i-го слоя, определяются по (6); 
; 
, 
, 
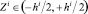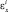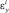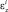– деформации в срединной поверхности i-го слоя.
В отличие от существующих выражений, в (4)–(7) появились слагаемые, учитывающие разномодульные свойства материала [5].
От напряжений в произвольной точке, интегрируя по толщине, переходим к записи погонных усилий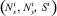 
и моментов 
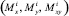, в i-м слое:
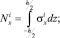
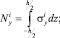
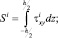
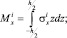
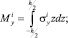
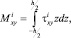(8)
где –h/2, h/2 – наибольшие расстояния от срединной поверхности до крайних волокон i-го слоя пластины.
Подставляя выражения для напряжений (7) в (8), после интегрирования (8) получим выражения для усилий и моментов в i-м слое:
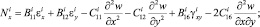
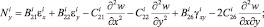(9)
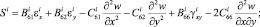
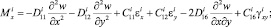
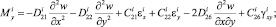
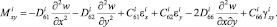
Здесь интегральные характеристики жесткости растяжения, сжатия, сдвига, изгиба и кручения определяются по следующим формулам:
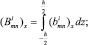
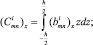
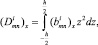(10)
где m, n = 1, 2, 6;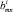 
– определяется из (6).
Аналогично (10) осуществляется интегрирование на площадке, ортогональной к оси Y. Выражения (9) позволяют в процессе изменения величины нагрузки во времени следить за изменением интегральных характеристик жесткости.
Появление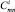 
связано с тем, что в материале, свойства которого на растяжение и сжатие различны, происходит смещение нейтральной поверхности по отношению к срединной. У большинства материалов отношение податливостей 
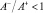, поэтому смещение происходит в сторону сжатых волокон. При этом деформации на уровне срединной поверхности не равны нулю.
Заключение
В результате проведенных исследований в известных формулах появились коэффициенты, учитывающие свойства разномодульности материала слоев.