Эредитарные процессы находят отражения в различных приложениях, например в книге В.В. Учайкина [9] эредитарным процессам посвящена целая глава. Понятие эредитарности или памяти было введено итальянским математиком Вито Вольтеррой для обобщения гармонического осциллятора заменой дифференциального уравнения на интегро-дифференциальное [3]. Далее в этой работе Вольтерра вывел обобщенный закон сохранения полной механической энергии для этой эредитарной колебательной системы. В отличие от закона сохранения энергии для гармонического осциллятора, обобщенный закон сохранения содержал дополнительное положительное слагаемое, которое отражает диссипацию энергии колебательной системы.
С точки зрения математического моделирования интегро-дифференциальные уравнения, которые описывают эредитарные колебательные процессы, удобно привести к дифференциальным уравнениям с производной дробного порядка [4]. Порядок дробной производной, в свою очередь, может зависеть от свойств среды [10].
В этой статье мы рассмотрим вопросы устойчивости нелинейного эредитарного осциллятора Ван-дер-Поля [5].
Основные определения
Отметим, что устойчивость нелинейных осцилляторов отличается от устойчивости линейных осцилляторов, так как необходимо исследовать не только их стационарные состояния, но и предельные циклы [11]. Устойчивость колебательной системы приводит к периодическим режимам, а неустойчивость - к хаотическим режимам. Дадим следующее определение эредитарной колебательной нелинейной системы.
Определение 1. Эредитарная нелинейная колебательная система может быть записана с помощью оператора производной дробного порядка Герасимова – Капуто:
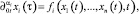
xi(0) = ci, i = 1, ..., n, (1)
где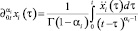 
– производные дробных порядков Герасимова - Капуто порядка 0 < αi < 2; ci – известные константы.
Отметим, что в работе [12] определение эредитарной колебательной системы было записано в терминах производной дробного порядка Римана – Лиувилля.
Ключевым объектом исследования в теории устойчивости динамических систем являются их точки равновесия.
Определение 2. Точки равновесия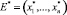 
эредитарной системы (1) являются решениями следующей системы алгебраических уравнений:
fi(x1(t), ..., xn(t), t) = 0. (2)
Эредитарная колебательная нелинейная система (1) может быть соизмеримой и несоизмеримой [12].
Определение 3. Эредитарная колебательная система (1) называется соизмеримой, если выполняется условие: α = ... =αn = α. Если выполняется условие: α ≠ ... ≠αn – несоизмеримой.
Дадим определение устойчивости предельного цикла [1, 2].
Определение 4. Предельный цикл является устойчивым, если существует такая область фазового пространства, которая содержит этот предельный цикл, что все фазовые траектории, начинающиеся в этой области, при t → ∞ асимптотически приближаются к предельному циклу. В противном случае предельный цикл называется неустойчивым.
Теоремы устойчивости эредитарных колебательных систем. В работе [12] были сформулированы и доказаны следующие две важные теоремы асимптотической устойчивости нелинейной эредитарной колебательной системы.
Теорема 1. Точки равновесия системы (1) называются асимптотически устойчивыми для соизмеримой системы, если собственные значения λi матрица Якоби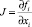 
, вычисленные согласно точкам равновесия E*, удовлетворяют следующим условиям:
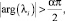i = 1, 2, ..., n. (3)
Теорема 2. Точки равновесия системы (1) называются асимптотически устойчивыми для несоизмеримой системы, где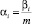 
, если выполняются следующие условия:
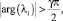i = 1, 2, ..., n, γ = 1/m, (4)
а λ вычисляется согласно характеристическому уравнению
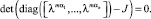(5)
Устойчивость эредитарного осциллятора Ван-дер-Поля. Пусть система (1) описывает эредитарный осциллятор Ван-дер-Поля:
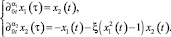(6)
Рассмотрим случай, когда система (6) соизмерима α1 = α2 = 1, т.е. случай классического осциллятора Ван-дер-Поля:
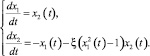(7)
Матрица Якоби системы (7) записывается следующим образом:
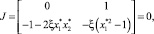(8)
где точки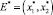 
– точки покоя системы (7). Из этой системы очевидно, что существует единственная точка покоя E* = (0, 0). Тогда характеристическое уравнение для системы (7) с учетом (8) имеет вид
λ2 – ξλ + 1 = 0. (9)
Можно убедиться, что корни характеристического уравнения (9) при ξ > 0 не удовлетворяют условиям теоремы 1. Действительно, в нашем случае имеет место неравенство:
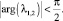
Поэтому точка равновесия системы E* = (0, 0) системы (7) будет неустойчивой, в частности, если 0 < ξ < 2 – неустойчивый фокус (рис. 1).
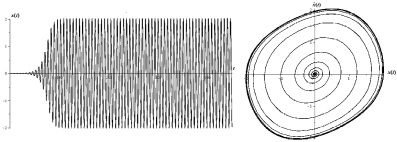
а б
Рис. 1. a – осциллограмма; б – фазовая траектория, полученные при ξ = 0,2 и (x0, y0) = (0,0001; 0,0001) для системы Ван-дер-Поля (7)
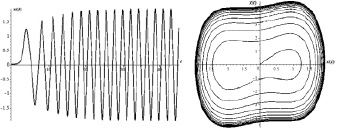
а б
Рис. 2. a – осциллограмма; б – фазовая траектория, полученные при ξ = 4 и (x0, y0) = (0,0001; 0,0001) для системы Ван-дер-Поля (7)
Осциллограмма и фазовая траектория на рис. 1 были получены с помощью явной конечно-разностной схемы, вопросы аппроксимации производных дробного порядка можно изучить в работах [6, 7].
Если ξ > 2, то точка покоя E* = (0, 0) системы (7) – неустойчивый узел (рис. 2).
Согласно определению 4 предельный цикл для системы Ван-дер-Поля (7) будет устойчивым, так как при t → ∞ фазовые траектории рис. 1, б и 2, б стремятся к предельному циклу изнутри. Если взять точку вне предельного цикла, то фазовые траектории будут стремиться при t → ∞ к нему извне (рис. 3).
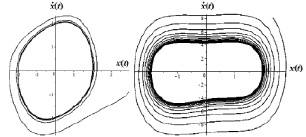
а б
Рис. 3. a – фазовая траектория с параметрами ξ = 0,2 и (x0, y0) = (3,96323; –0,8901); б – фазовая траектория с параметрами ξ = 4 и (x0, y0) = (2,35028; 8,075) для системы Ван-дер-Поля (7)
Рассмотрим случай эредитарного осциллятора Ван-дер-Поля, характеризующийся несоизмеримой системой (6), в которой α = 0,5; β = 1 и γ = 1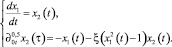/10:
(10)
С учетом (8) характеристическое уравнение для системы (10) имеет вид
λ25 – ξλ10 + 1 = 0. (11)
Пусть управляющий параметр ξ = 4, тогда два корня,
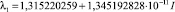
и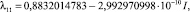 
характеристического уравнения (11) не удовлетворяют условиям теоремы 2, т.е. выполняется неравенство
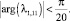
Так как действительные части корней λ1 и λ11 положительны, то точка состояния равновесии системы E* = (0, 0) является неустойчивым фокусом. Однако фазовая траектория стремится к предельному циклу (рис. 4).
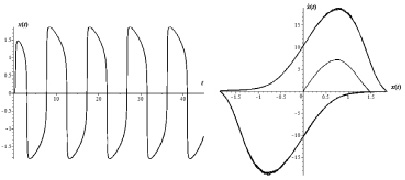
а б
Рис. 4. a – осциллограмма; б – фазовая траектория, полученные при ξ = 4 и (x0, y0) = (0,0001; 0,0001) для системы Ван-дер-Поля (10)
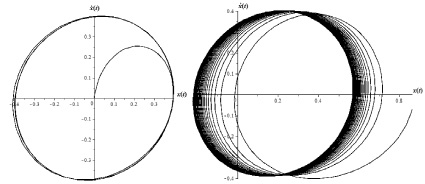
а б
Рис. 5. Фазовая траектория (а) с начальной точкой внутри предельного цикла (x0, y0) = (0, 0) и фазовая траектория (б) с начальной точкой вне предельного цикла: (x0, y0) = (0,862; −0,67)
Рассмотрим случай, когда в соизмеримой системе (7) действует внешняя периодическая сила: f(t) = δ sin(ωt). Система записывается так:
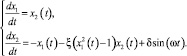(12)
В системе (12) положим следующие значения параметров: ξ = 0,2; δ = 0,4; ω = t = 1. Получим точку равновесия системы E* = (–0,336; 0), которая является неустойчивым фокусом. В случае несоизмеримой системы: α = 1,2 и β = 0,2 мы получаем следующее характеристическое уравнение:
λ24 – 0,4λ2 + 1 = 0. (13)
Все корни уравнения (13) удовлетворяют условию (4), поэтому точка равновесия E* асимптотически устойчива. Необходимо заметить, что фазовая траектория выходит на устойчивый предельный цикл (рис. 5).
Заключение
В работе были рассмотрены вопросы устойчивости нелинейных эредитарных колебательных систем на примере эредитарного осциллятора Ван-дер-Поля. С помощью теорем для соизмеримой и несоизмеримых систем были исследованы точки покоя осциллятора Ван-дер-Поля, а также показано, что фазовая траектория выходит на устойчивый предельный цикл.
В продолжении работы имеет определенный интерес исследование вопроса об устойчивости нелинейных эредитарных осцилляторов с переменными порядками дробных производных [8].