Для улучшения физико-механических и эксплуатационных свойств бетонов используются различные методы. Одним из таких методов является применение наполнителей. Наполнители различной природы и зернового состава позволяют целенаправленно регулировать структуру и свойства цементного камня бетона [2, 3, 4, 5, 6, 7, 10].
Цель исследования – изучение влияния зернового состава наполнителя из известняка речного на теплопроводность цементных композитов.
Таблица 1
Химический состав известняка речного
|
Наполнитель |
п.п.п |
SiO2 |
Al2O3 |
Fe2O3 |
CaO |
MgO |
SO3 |
K2O |
Na2O |
Cl– |
W |
|
Известняк речной |
43,77 |
0,29 |
0,09 |
0,09 |
51,50 |
4,52 |
0,18 |
0 |
0,04 |
0,007 |
0,65 |
Материалы и методы исследования
В качестве наполнителя для получения опытных образцов цементных композитов использовался известняк речной, химический состав которого приведен в табл. 1.
Зерновой состав наполнителя варьировался путем смешивания трех фракций с размером зерен 0,63–0,315, 0,315–0,16 и менее 0,16 мм.
Методика для определения теплопроводности опытных образцов основывалась на использовании выражения
λ = a·Сp·ρ,
где а – температуропроводность, м2/с; Сp – удельная теплоемкость, Дж/(кг K); ρ – плотность материала, кг/м3.
На стадии подготовки к экспериментам по определению теплопроводности определялись геометрические размеры и масса образцов. В каждом образце закреплялась калиброванная термопара «медь-константан» для регистрации температуры с помощью аналого-цифрового преобразователя с записью данных в файл.
Плотность материала образцов определялась по формуле
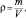
где m – масса образца, кг; V – объем образца, м3.
Определение удельной теплоемкости Сp осуществлялось калориметрическим способом исходя из уравнения теплового баланса. Для получения экспериментальных данных исследуемый образец с закрепленной термопарой нагревали до 100 °С, после чего помещали в мерную емкость, заполненную жидкостью с фиксированной начальной температурой.
В экспериментах регистрировали две временные зависимости: динамику нагрева жидкости в мерной ёмкости (изменение температуры жидкости) и температуру образца (значение показаний термопары). Для снижения потерь, связанных с теплоотдачей в окружающую среду, мерная емкость экранировалась алюминиевой фольгой.
Уравнение теплового баланса для данной системы (мерная ёмкость с жидкостью и образец строительного материала) имеет вид
Cp1·m1(tk – θ) = (Cp2·m2 + Cp3·m3) Δt,
где Cp1 – определяемая удельная теплоемкость образца; m1 – масса образца; Cp2 – теплоемкость мерной емкости (справочные данные); m2 – масса мерной емкости; Cp3 – теплоемкость жидкости в емкости (справочные данные); m3 – масса жидкости в мерной емкости; Δt – перепад температуры в емкости после помещения в нее образца, нагретого предварительно до 100 °С; θ = t + Δt – конечная температура образца и жидкости; t – температура жидкости в емкости до погружения образца; tk – температура образца до погружения в охлаждающую жидкость.
Температуропроводность определялась согласно [9, 8] с использованием выражения
a = K·m,
где К – коэффициент формы при регулярном режиме охлаждения; т – темп охлаждения, 1/c.
Для образца в форме параллелепипеда со сторонами l1, l2, l3 величина коэффициента формы согласно [9, 8] может быть определена аналитически исходя из зависимости
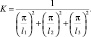
Темп охлаждения для регулярного режима согласно [9] определялся из зависимости
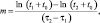
где t1 и t2 – температура в данной точке образца в момент времени τ1 и τ2; t0 – температура охлаждающей среды, в качестве которой использовалось трансформаторное масло (возможной альтернативой является кремнийорганическая жидкость).
Вид теоретической кривой временной зависимости охлаждения образца, используемой для определения темпа охлаждения исследуемого образца, приведен на рис. 1.
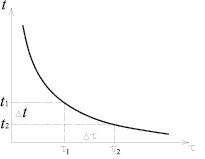
Рис. 1. Вид теоретической кривой временной зависимости охлаждения образца
Изучение влияния зернового состава наполнителя из известняка речного при возможно более полном заполнении им объема материала цементных композитов на их теплопроводность проводили методом математического планирования эксперимента с использованием симплекс-решетчатого плана Шеффе [1]. Объемные доли наполнителя и остальных компонентов цементного композита, располагающихся в пустотах между зернами наполнителя, во всех опытах оставались постоянными. В процессе экспериментов зерновой состав наполнителя изменяли путем смешивания в заданных соотношениях трех фракций Х1, Х2 и Х3 узкого зернового состава с размером зерен соответственно, 0,63–0,315, 0,315–0,16 и менее 0,16 мм. Изменяющаяся объемная доля каждой из смешиваемых фракций наполнителя в цементном композите принималась за контролируемую переменную. При условии, что теплопроводность наполненного композита зависит только от соотношения смешиваемых фракций наполнителя, факторное пространство представляет собой правильный 2-мерный симплекс. Для системы фракций наполнителя выполняется соотношение
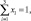
где хi ≥ 0 – объемная доля (концентрация) фракции наполнителя.
При количестве фракций равном трем правильный симплекс – равносторонний треугольник. Вершины треугольника соответствуют одной фракции, стороны – двойным системам, точка внутри треугольника отвечает одному определенному составу тройной системы.
Результаты исследования и их обсуждение
Матрица планирования и результаты эксперимента приведены в табл. 2.
Для вычисления теплопроводности наполненных композитов использовались данные, приведенные в табл. 3.
Статистическая обработка результатов эксперимента позволила получить зависимость в виде полинома 3 порядка для 3-фракционной смеси, характеризующей изменение теплопроводности наполненных известняком речным цементных композитов от зернового состава наполнителя:
λ = 0,311х1 + 0,245х2 + 0,207х3 + 0,025х1х2 – 0,11х1х3 + 0,072х2х3 + + 0,277х1х2(х1 – х2) – 0,106х1х3(х1 – х3) + 0,603х2х3 (х2 – х3) + 1,381х1х2х3.
Таблица 2
Матрица планирования и результаты эксперимента
|
Номер опыта |
Концентрация фракций |
Теплопроводность наполненных композитов, λ, Вт/м·К |
||
|
Х1 |
Х2 |
Х3 |
||
|
1 |
1 |
0 |
0 |
0,311 |
|
2 |
0 |
1 |
0 |
0,245 |
|
3 |
0 |
0 |
1 |
0,207 |
|
4 |
1/3 |
2/3 |
0 |
0,252 |
|
5 |
1/3 |
0 |
2/3 |
0,225 |
|
6 |
0 |
1/3 |
2/3 |
0,191 |
|
7 |
2/3 |
1/3 |
0 |
0,315 |
|
8 |
2/3 |
0 |
1/3 |
0,244 |
|
9 |
0 |
2/3 |
1/3 |
0,293 |
|
10 |
1/3 |
1/3 |
1/3 |
0,304 |
Таблица 3
Данные, использованные для вычисления теплопроводности наполненных композитов
|
Номер образца |
Размеры, м·103 |
Объем, м3·10–6 |
Масса, кг·10–3 |
Плотность, кг/м3 |
Теплоемкость, Дж/(кг·°С) |
Темп охлаждения*, 1/с |
Температуропроводность, м2/с·106 |
Теплопроводность, Вт/(м·К) |
|
1 |
30×10×10 |
3,0 |
5,84 |
1945 |
1185 |
0,028 |
0,1345 |
0,311 |
|
2 |
30×10×10 |
3,0 |
6,15 |
2050 |
1130 |
0,022 |
0,1055 |
0,245 |
|
3 |
30×10×10 |
3,0 |
5,68 |
1890 |
1075 |
0,021 |
0,101 |
0,207 |
|
4 |
31×10×10 |
3,1 |
6,15 |
1985 |
1105 |
0,024 |
0,115 |
0,252 |
|
5 |
30×10×10 |
3,0 |
5,76 |
1920 |
1234 |
0,02 |
0,097 |
0,225 |
|
6 |
30×10×10,5 |
3,15 |
6,1 |
1935 |
1210 |
0,017 |
0,0815 |
0,191 |
|
7 |
30,5×10×11 |
3,36 |
6,42 |
1915 |
1545 |
0,022 |
0,1055 |
0,315 |
|
8 |
30,5×10×11 |
3,36 |
6,52 |
1940 |
1390 |
0,019 |
0,091 |
0,244 |
|
9 |
30×10×11 |
3,3 |
6,25 |
1890 |
1130 |
0,0257 |
0,127 |
0,293 |
|
10 |
30,5×10×11 |
3,36 |
6,41 |
1910 |
1330 |
0,025 |
0,12 |
0,304 |
Примечание. *для вычисления темпа охлаждения образцов использовали временные зависимости охлаждения образцов на участке регулярного режима охлаждения.
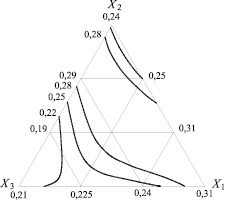
Рис. 2. Линии равных значений теплопроводности наполненных известняком речным цементных композитов на концентрационном треугольнике
По полученным уравнениям регрессии были построены графики в виде линий равных значений теплопроводности, представленные на рис. 2.
Результаты проведенных экспериментов показали (рис. 2), что теплопроводность исследованных образцов изменяется в пределах от 0,19 до 0,31 Вт/(м?К). Обращает на себя внимание тенденция увеличения теплопроводности при уменьшении дисперсности наполнителя в случае использования в качестве наполнителя одной из фракций Х1, Х2 или Х3, а также двухфракционных смесей, включающих фракцию Х1 (см. рис. 2: значения теплопроводности в вершинах и на сторонах Х1–Х2 и Х1–Х3 концентрационного треугольника). В области трёхфракционных и двухфракционных с фракциями Х2 и Х3 смесей наполнителя имеется локальный участок, на котором тенденция возрастания теплопроводности при уменьшении дисперсности наполнителя не прослеживается.
Выводы
1. Методом математического планирования эксперимента исследовано влияние зернового состава известнякового наполнителя при возможно более полном заполнении им объема материала цементных композитов на их теплопроводность.
2. Путем реализации симплекс-решетчатого плана эксперимента для системы трех фракций наполнителя установлена зависимость теплопроводности от зернового состава наполнителя, который изменялся путем смешивания трёх его фракций в заданных пропорциях.
3. Для исследованной области варьирования зернового состава наполнителя теплопроводность наполненных цементных композитов изменяется в пределах от 0,19 до 0,31 Вт/(м·К).
4. Минимальная теплопроводность достигается при использовании наполнителя, состоящего из 2/3 части (по объему) фракции непрерывного зернового состава с максимальным размером зерен 0,16 мм и 1/3 части фракции 0,315–0,16 мм.
5. Максимальная теплопроводность соответствует составам с наполнителем фракции 0,63–0,315 мм.



