На сегодняшний день существует множество моделей и типов искусственных нейронных сетей, различных по своей структуре и функционалу [2]. Из всего многообразия архитектур особняком стоят сети Хопфилда, которые, наряду с алгоритмом Back Propagation, в 70-х годах возродили интерес в области искусственных нейронных сетей (ИНС) после многолетнего спада. Сети Хопфилда обладают свойством за конечное число тактов переходить из произвольного начального состояния в состояние устойчивого равновесия, называемого аттрактором или точкой равновесия. Точка равновесия соответствует одному из множества первоначально предъявленных сети образов и достигается при предъявлении на входы сети как идеальных, так и зашумленных объектов для распознавания.
Целью работы является модернизация классической сети Хопфилда для увеличения её производительности на основе информационных свойств воды.
Материалы и объекты исследования
Сеть Хопфилда состоит из единственного слоя нейронов, число которых N совпадает с размером запомненных и распознаваемых образов. Выход каждого нейрона соединяется с входами всех нейронов сети, за исключением самого себя. Таким образом, каждый нейрон имеет N – 1 вход, с соответствующим весовым коэффициентом w, а вход, соответствующий номеру самого нейрона, смысловой нагрузки не имеет. Входные сигналы – образцы – подаются, по сути, на выходы сети, а оттуда по обратным связям передаются во все нейроны одновременно. Структурная схема сети Хопфилда представлена на рис. 1.
Обрабатываемые сетью элементы могут быть представлены N-мерным вектором Х = {x1, x2,…, xN}. Каждый элемент xi имеет одно из двух значений: +1 или –1. Множество векторов {X1, X2, …, Xm,…, XM} составляют обучающую выборку, где M – число запомненных сетью образов. Если входной образ распознан, выход сети равен некоему Y = Xm, где Y – вектор выходных значений сети: Y = {y1, y2,…, yN} той же размерности.
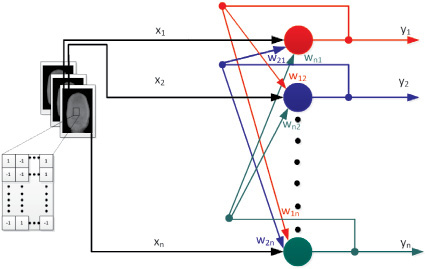
Рис. 1. Сеть Хопфилда
Для реализации рекурсивного характера функционирования сети на однопроцессорных архитектурах вводится понятие внутреннего состояния нейрона s, которое изменяется после подачи на вход очередного входного вектора и передаётся на выход нейрона после того, как все нейроны сети обработали один и тот же входной сигнал. Такой режим функционирования получил название синхронного, в противовес асинхронному – не нуждающемуся в наличии состояния, поскольку обработанное значение передаётся непосредственно на выход нейрона.
Расчёт весовых коэффициентов, соответствующий процессу обучения сети или запоминания эталонных образов, производится однократно.
Функционирование сети в режиме распознавания входных векторов продолжается до тех пор, пока выходные значения всех нейронов на очередном шаге итерации не совпадут со значениями предыдущего шага. При очевидном достоинстве – простоте реализации ассоциативной памяти – сеть Хопфилда имеет значительные недостатки, затрудняющие её широкое применение в системах распознавания образов различной природы. К таким недостаткам относятся: возможность зацикливания сети при использовании коррелированных векторов-образцов; хранение в памяти сети не только эталонных образов, но и их негативов; достижение устойчивого состояния, не соответствующего ни одному из запомненных ранее образов [3]. И главный недостаток – граница ёмкости сети (т.е. количество образов, которое она может запомнить) – по разным оценкам, составляет 12–15 % от общего числа нейронов N.
Исследование авторами сетей Хопфилда, обученных по классическому алгоритму расчёта весовых коэффициентов [1]:
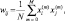
подтвердило указанные недостатки и сместило границу ёмкости до 10–12 %. В качестве образцов для запоминания использовались чёрно-белые отпечатки пальцев размером 2,34 Кб. Столь малая ёмкость обусловлена тем, что предъявленные сети образцы для запоминания достаточно сильно коррелированы и весьма далеки от ортогональности.
Результаты исследования и их обсуждение
Для увеличения числа хранимых образов и повышения качества распознавания предлагаются различные способы, которые можно разделить на две группы. К первой группе относятся решения, связанные с модификацией формулы расчёта матрицы коэффициентов [1]. Ко второй группе относятся решения, связанные с увеличением числа слоёв сети [3].
Авторы предлагают решение, которое предполагает изменение числа связей (увеличение) в однослойной сети Хопфилда, по сути своей относящееся к первой группе, поскольку введение дополнительной связи между нейроном i и нейроном j, уже имеющим первоначальные связи wij = wji, будет соответствовать их перерасчёту. Введение новых связей может быть как однонаправленным (от нейрона i к нейрону j), так и двунаправленным.
Увеличение числа связей сети Хопфилда будет осуществляться на основе идеи информационных свойств воды, впервые описанных в [5] японским исследователем М. Эмото. В лаборатории доктора Эмото были исследованы образцы воды из различных водных источников всего мира; вода подвергалась различным видам воздействия, таким как музыка, изображения, электромагнитное излучение от телевизора или мобильного телефона, мысли одного человека и групп людей, молитвы, напечатанные и произнесенные слова на разных языках. В [5] Эмото приводит доказательства информационных свойств, важнейшими из которых является то, что:
1) никакие два образца воды не образуют полностью одинаковых кристаллов при замерзании;
2) форма кристаллов отражает свойства воды и, в частности, сохраняет информацию о том или ином воздействии, оказанном на воду.
Информационные свойства воды в 80-х гг. прошлого века изучала группа исследователей из академии РАМН под руководством В.П. Казначеева [4]. Казначеевым был продемонстрирован перенос биологической информации из одной герметичной водной среды в другую, между которыми существовал только оптический контакт. Гибель зараженных биоматериалов первой ёмкости сопровождалась гибелью здоровых клеток в соседней камере.
По мнению авторов, использование пусть ещё не до конца изученных информационных свойств воды может помочь в снижении негативных эффектов распознавания и увеличении ёмкости исследуемой сети.
Дополнительные связи между элементами сети предлагается формировать по аналогии со связями:
а) между атомами молекулы воды;
б) между молекулами внутри кристалла.
В этом случае сеть рассматривается не как линейный слой нейронов, а как матрица размером k×r, где k, r – размеры образа по горизонтали и вертикали.
В первом случае три нейрона сети, соединенные в «молекулу», ассоциируются с одним атомом кислорода и двумя атомами водорода. Возможные способы ориентации атомов приведены на рис. 2. «Слой воды», распределяемый по поверхности сети Хопфилда, может иметь различную «высоту», т.е. одни и те же нейроны могут входить в состав разных молекул. Расположение молекул может быть равномерным или хаотичным. Длина связей в молекулах может иметь единичную и произвольную длину. При создании дополнительных связей могут использоваться молекулы одного или разных типов. Связи между элементами внутри молекулы, как уже упоминалось ранее, могут быть одно- и двунаправленными.
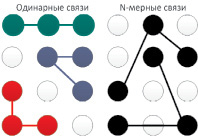
Рис. 2. Ориентация атомов в связях по типу молекулы H2O
Расчёт весовых коэффициентов дополнительных связей может быть осуществлен по формуле (2) или её возможным модификациям:
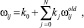 (2)
(2)
где 0 ≤ k0 ≤ 1, 0 ≤ kj ≤ 1.
Во втором случае несколько нейронов сети будут объединяться в правильный кристалл или «снежинку». Связи в снежинке будут располагаться от центра к каждому лучевому нейрону (радиальная структура) либо иметь произвольную структуру (рис. 3).
Расположение снежинок, как и молекул воды, может быть случайным и упорядоченным, однослойным и многослойным. Кроме того, снежинки можно располагать в форме «сугробов», т.е. там, где информационная область образов выше, слой кристаллов может иметь большую высоту. Как и в случае молекул, одновременно могут использоваться однотипные и разнообразные кристаллические структуры, с одно- и двунаправленными связями.
Для реализации экспериментов с предложенным многообразием архитектур была разработана объектная модель сети Хопфилда, позволяющая оперировать различными классами сетей, связанных механизмом наследования.
Ниже представленный фрагмент кода отображает интерфейс классов верхнего уровня – класс «Нейрон» и класс «Сеть», связанных отношением агрегации.
Предложенная модель легла в основу инструментальной программной системы, предназначенной для проведения серии экспериментов с классическим вариантом сети TNet и различными модификациями сетей, полученных в результате наследования от класса TWaterNet.
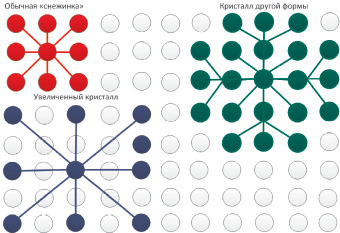
Рис. 3. Кристаллы воды
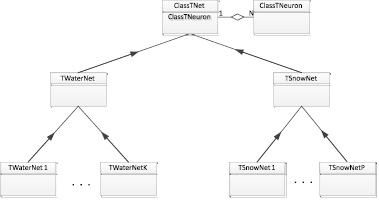
Рис. 4. Структура классов для анализа модифицированных сетей


Серия экспериментов с чёрно-белыми объектами размером 40×60 пикселей (2,34 кБ), содержащими рисунок папиллярных узоров, показала, что сети типа TWaterNet уверенно запоминают и впоследствии распознают около 450 идеальных или 420 слабо искаженных (до 4 %) объектов, что составляет соответственно 17 % от общего числа нейронов сети, равного 2400.
Заключение
Предложенный способ реализации расчёта коэффициентов сети Хопфилда на основе введения дополнительных связей между нейронами сети по типу связей в молекуле воды на примере распознавания папиллярных рисунков показал очевидную стабильность в работе сети как в синхронном, так и асинхронном режимах. Успешные эксперименты с достаточно простым способом введения дополнительных связей позволяют сделать заключение о целесообразности разработки объектов класса TSnowNet и их дальнейшего исследования.



