Мультипроектное планирование решает взаимосвязанные проблемы – формирование календарного графика [2] и распределение ресурсов [8]. Один из подходов к решению этих проблем использует агрегированные представления проектов [1, 2].
Календарные графики мультипроектного планирования относятся к расписаниям иерархических или сетевых структур действий [3]. Формирование расписания – это определение времен начала выполнения всех действий или их совокупностей в интервале расписания [5]. Для мультипроектного планирования необходимо решение двух задач:
1) агрегирование заявок проекта – определение относительных начальных времен выполнения каждой работы в пределах интервала расписания проекта (длительности критического пути графа проекта или задаваемой/переопределяемой длительности);
2) формирование календарного графика мультипроектного планирования – определение относительных начальных времен выполнения агрегаций заявок проектов в пределах задаваемого или определяемого интервала расписания.
Статья посвящена решению первой задачи, а ее целью является представление подходов к программному формированию агрегаций проектов – оптимизированных календарных графиков проектов для произвольного количества заявок.
Общие подходы
Агрегирование является задачей управления одним проектом, но в отличие от [4] необходимы допущения. На данном этапе исследования интервал расписания агрегации принят равным критическому пути графа проекта. В получаемых решениях разрешено превышение потребляемых ресурсов на отдельных тактах планирования по сравнению с уровнями выделяемых проекту ресурсов. В последующем мультипроектном планировании эти превышения будут удовлетворяться совместно используемыми выделяемыми ресурсами. Интервалы, в пределах которых могут «мигрировать» работы, не находящиеся на критическом пути, позволяют осуществить варьирование агрегаций.
Алгоритмизация и разработка программного обеспечения агрегирования проектов использовали следующие концепции [3]: программное решение задачи в рамках СУБД; двухэтапный процесс решения; идеология жадного алгоритма; концепции загруженности и равномерности; использование методов ранжирования теории принятия решений.
Два этапа решения включают формирование начальной агрегации и ее последующую оптимизацию. Методы этапов цикличны и завершаются после включения всех заявок проекта в начальную агрегацию или при невозможности дальнейшего улучшения агрегации.
Формирование начальной агрегации решается последовательным выбором очередной заявки проекта и последующим ее включением в календарный график в определяемое время начала выполнения работы. Выбор заявки проекта базируется на концепции загруженности. Выбор времени включения этой заявки использует концепцию равномерности. В каждом цикле присутствуют две операции выбора с принятием некоторых решений.
Задача оптимизации начальной агрегации решается последовательным выбором наиболее неравномерной работы проекта и последующей ее перестановкой в графике в выбираемое время начала выполнения работы. Перестановка работы в календарном графике агрегации также базируется на концепции равномерности. В каждом цикле также присутствуют две операции выбора. Такой подход характерен для жадных алгоритмов [4, 8], предполагающих цикличность обоих этапов задачи формирования агрегации проекта [4].
Операции выбора в представляемых алгоритмах являются многокритериальными [6], и для их реализации привлечен аппарат методов ранжирования. В представляемых алгоритмах использованы методы, в основе которых лежит метод «жесткого» ранжирования [7]. В дальнейшем под термином многокритериальное ранжирование будет пониматься «жесткое» ранжирование. Будут различаться прямое (по «возрастанию») и обратное (по «убыванию») многокритериальное ранжирование.
Постановка и формализация задачи
Введем необходимые в дальнейшем обозначения.
Исходные данные задачи:
I – количество проектов мультипроектного планирования;
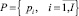– множество проектов мультипроекта;
nei – количество работ проекта pi;
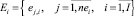– множество работ проекта pi (j = 1 – источник, j = nei – сток);
индекс работы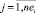 
имеет различный характер в зависимости от решаемой задачи: идентификатор работы в соответствующей таблице БД; идентификатор работы в множестве работ проекта; идентификатор работы в множестве работ пути графа проекта; порядковый номер работы при ее включении в начальную агрегацию; порядковый номер работы при оптимизации начальной агрегации;
epj,i – количество непосредственных предшественников работы ej,i;
EPj,i – множество непосредственных предшественников работы ej,i, EPj,i ∈ Ei;
efj,i – количество непосредственных последователей работы ej,i;
EFj,i – множество непосредственных последователей работы ej,i, EFj,i ∈ Ei;
u – количество типов возобновляемых ресурсов;
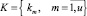– множество типов возобновляемых ресурсов;
Rm,i,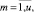 
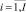– объем ресурса типа km, выделяемый проекту pi во время его выполнения на каждом такте планирования;
rm,j,i,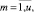 
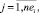
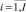– объем ресурса типа km, требуемый работе ej,i проекта pi во время ее выполнения на каждом такте планирования;
dj,i,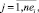 
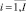– длительность (трудоемкость) выполнения работы ej,i проекта pi, такты планирования.
Исходные расчетные данные задачи:
Cpi,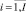 
– критический путь проекта pi, такты планирования;
Di – трудоемкость проекта pi. В предлагаемом решении Di = Cpi = Int,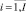 
.
Переменные задачи:
ni,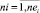 
– количество: включенных в начальную агрегацию работ проекта pi; переставленных работ проекта pi в календарном графике агрегации;
nr,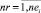 
– количество: не включенных в начальную агрегацию заявок проекта pi; не оптимизированных работ проекта pi в календарном графике агрегации;
на любом шаге формирования и оптимизации начальной агрегации ni + nr ≡ nei;
tij,i – минимально возможный такт включения работы ej,i в агрегацию проекта pi:
tfj,i – максимально возможный такт включения работы ej,i в агрегацию проекта pi:
tj,i – начальный такт выполнения работы ej,i проекта pi в календарном графике агрегации;
Rmaxm,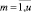 
– максимальный тактовый объем потребляемого ресурса типа km в календарном графике агрегации;
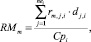
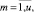
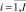– средний объем ресурса типа km, потребляемый работами проекта pi в интервале расписания;
RSm,j,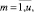 
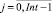– объем ресурса типа km, потребляемый календарным графиком агрегации на j-м такте интервала расписания;
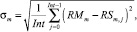
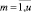– среднеквадратичное отклонение потребления ресурса типа km на всех тактах интервала расписания от среднего значения потребления этого ресурса в расписании.
Задача формирования начальной агрегации проекта pi состоит в цикличном выборе очередной, не находящейся на критическом пути, заявки проекта и формировании расписания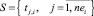 
, которое минимизирует вектор максимальных тактовых объемов потребляемых ресурсов внутри критического пути (интервала расписания)
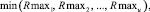(1)
при обязательных ограничениях
;
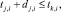
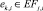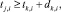
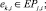(2)
;
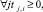
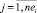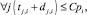
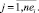(3)
Целевая функция (1) минимизирует верхнее отклонение потребляемых ресурсов, что достаточно для формирования начальной агрегации проекта при включении очередной работы заявки в календарный график. Целевая функция связана с необходимостью многокритериального ранжирования векторов (1). Неравенства ограничений (2) отражают отношения следования и предшествования работ проекта. Неравенства ограничений (3) отражают безусловность нахождения работ проекта внутри интервала расписания.
Интервалы включения заявок ej,i в календарный график агрегации определяются следующими выражениями:
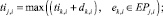(4)
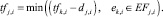(5)
Минимально возможные такты включения (4) определяются для всех заявок от источника до стока, для непосредственных последователей источника tik,i = 0. Максимально возможные такты включения (5) определяются в обратном порядке – от стока до источника. Для непосредственных предшественников стока tfk,i = Cpi.
Оценки загруженности cj,m,i заявки ej,i проекта pi на очередном шаге формирования начальной агрегации определяется объемом требуемого ресурса
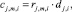
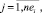
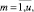
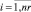. (6)
Оценки загруженности (6) формируют множество векторов (критериев загруженности) заявок на очередном шаге формирования календарного графика начальной агрегации:
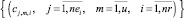(7)
Обратное многокритериальное ранжирование векторов (7) порождает множество рангов заявок
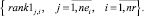(8)
Старшая по рангу заявка проекта становится очередным кандидатом на включение в начальную агрегацию проекта pi.
Для определения времени включения tni+1,i работа eni+1,i последовательно, по одному такту перемещается с учетом ограничений (2), (3) внутри интервала [tini+1,i, tfni+1,i], формируя множество векторов:
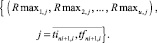(9)
Прямое многокритериальное ранжирование векторов (9) определяет доминирующий вектор, индекс j которого определяет искомое начальное время включения работы eni+1,i в календарный график начальной агрегации tni+1,i = j.
Очередной шаг формирования начальной агрегации завершается переопределением tfj,i для работ, предшествующих от источника. Для работ, непосредственно предшествующих eni+1,i, в выражениях (5) применяется tni+1,i. Также осуществляется переопределение tij,i для работ, следующих от eni+1,i до стока. Для работ, непосредственно следующих от eni+1,i, в выражениях (4) применяются tik,i = tni+1,i и dk,i = dni+1,i. Если nr > 0, то переход к следующему шагу формирования начальной агрегации.
Задача оптимизации начальной агрегации проекта pi состоит в изменении начальной агрегации для формировании расписания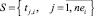 
, которое минимизирует вектор среднеквадратичных отклонений потребления ресурсов 
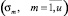на всех тактах интервала расписания от средних значений потребления ресурсов расписания
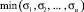(10)
при обязательных ограничениях (2), (3).
Целевая функция (10), являясь интегральной оценкой календарного графика, минимизирует все отклонения. Целевая функция связана с необходимостью многокритериального ранжирования получаемых на ее основе векторов (10).
Оценка равномерности n-го такта работы ej,i проекта pi по ресурсу km на очередном шаге оптимизации начального календарного графика агрегации определяется следующим выражением:
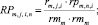
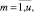
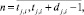
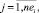
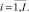(11)
Значения тактовых оценок равномерности находятся в интервале [0, 1]. Чем больше величина оценки (11), тем неравномернее соответствующая работа проекта на данном такте интервала расписания по данному ресурсу. Оценки равномерности проектов (11) формируют u множеств векторов (критериев равномерности) работ проекта по каждому ресурсу.
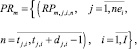
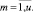(12)
Прямое многокритериальное ранжирование векторов (12) проектов расписания порождает множества рангов векторов работ проекта по каждому ресурсу
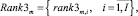
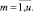(13)
Ранги векторов (13) формируют множество векторов (критериев равномерности) неоптимизированных работ проекта
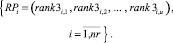(14)
Старшая по рангу работа проекта, полученная прямым многокритериальным ранжированием векторов (14), является самой неравномерной среди неоптимизированных при принятых оценках и критериях равномерности. Она становится очередным кандидатом eni+1,i на перестановку в календарном графике агрегации.
Для определения начального времени TIni+1 перестановки работа eni+1,i проекта pi последовательно, по одному такту перемещается с учетом ограничений (2), (3) внутри интервала расписания, формируя множество векторов:
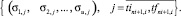(15)
Прямое многокритериальное ранжирование векторов (15) определяет доминирующий вектор, индекс j которого определяет искомое начальное время для перестановки работы eni+1,i проекта pi в календарном графике tni+1,i = j. Очередной шаг оптимизации завершается переопределением tfj,i и tij,i, и если nr > 0, то переход к следующему шагу.
Реализация и численные результаты
Для численных экспериментов использовались случайно выбранные из библиотеки тестовых задач PSPLib проекты. Проекты включают по 30 работ и для своего выполнения им необходимо 4 типа ресурсов.
На рис. 1 представлена начальная агрегация одного из проектов. В левой части представлена диаграмма Ганта работ выбранного проекта. Работы критического пути выделены красным цветом. Оставшиеся работы проекта размещены внутри интервалов их возможного перемещения.
В правой части представлены агрегации проекта по каждому из четырех ресурсов. Для каждого ресурса красной линией с цифровым обозначением показаны уровни выделяемых проекту объемов каждого такта. В каждой из агрегаций представлена величина среднеквадратичного отклонения в %.
На рис. 2 представлена оптимизированная агрегация этого же проекта.
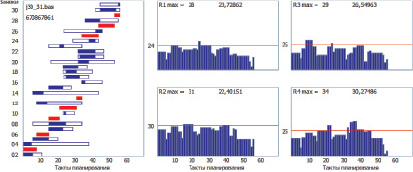
Рис. 1. Начальная агрегация проекта
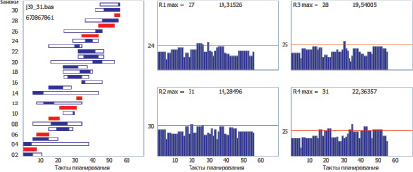
Рис. 2. Оптимизированная агрегация проекта
Заключение
Авторы считают, что новыми являются следующие положения и результаты:
- осуществлена формализация задач формирования и оптимизации календарного графика агрегации проекта;
- представлены общие подходы и алгоритмы решения задач формирования календарных графиков агрегаций с использованием методов ранжирования теории принятия решений.