Сама сущность современных персональных компьютеров делает их зависящими от систем счисления и от правил, которые определяют связь между числами. Однако, остаточная система, или система остаточных классов, которая является темой этой статьи, представляет дополнительное отклонение от двоичной и десятичной систем чисел, чем последняя друг от друга, так как некоторые основные концепции, такие как использование фиксированных оснований (например, 10 или 2). В результате этих основных различий остаточная арифметика, которая является манипуляцией чисел, выраженных в системе остаточных классов, предлагает необычный набор характеристик. Например, остаточная арифметика обеспечивает возможность суммировать, вычитать или умножать в один этап, невзирая на протяженность чисел, не прибегая к промежуточным цифрам переноса или внутренним задержкам. Таким образом, скорее изменением в системе чисел, чем добавлением логических схем и оборудования, возможно в принципе заставить компьютер работать быстрее. К сожалению, остаточная арифметика также имеет атрибуты, которые являются затруднительными и убыточными настолько, что на практике технология использования не всегда возможна.
Рассмотрим некоторые свойства остаточной арифметики в сравнении с традиционными системами счисления. Для проведения сравнения рассмотрим свойства десятичной системы. Как будет видно далее, система остаточных чисел не имеет всех этих свойств.
Любое положительное целое число х может быть записано в виде
x = + (αn10n + αn-110n-1 + … + α110 + α0), (1)
где αi – это целые десятичные цифры в интервале [0, 9]. Очевидно, что десятичная система счисления не имеет пределов, т.е. любое целое число, невзирая на его значение, может быть выражено в системе. Более того, это уникальное представление, в котором каждое целое число имеет только одно представление. Однако, в отличие от других систем счисления, десятичное представление является безызбыточным, т.е. каждое сочетание αi цифр представляет число и два разных набора αi, не относящихся к одному и тому же числу.
Десятичная система имеет представление весового числа; каждая цифра αi умножается на постоянную величину в определяемой связи. В этом случае постоянная величина или вес – это 10i, а основания степени есть основание системы, то есть 10. Все веса, используемые в этой системе, – это степени одного и того же основания. Такие числовые системы называются системами с фиксированным основанием.
Введем некоторые отличительные свойства систем счисления.
Предел числовой системы определяется как интервал, над которым каждое целое число может быть представлено системой за неимением двух чисел с одним и тем же представлением. Очевидно, что десятичная система имеет неопределенные границы, однако в практике применяются усеченные системы чисел, потому что физические системы могут вместить только ограниченное число цифр. Так в компьютерах числовой предел определяется точно положением длины слова и типом используемой системы счисления.
Представление числа называется уникальным, если каждое число в системе имеет только одно представление. Например, двоичная система счисления, часто используемая в компьютерах, является уникальной. Однако многие обычно используемые системы чисел не являются уникальными. Например, десятичная система счисления, расширенная для включения отрицательных чисел, обычно имеет два представления для нуля: + 0 и – 0. Очевидно, что любая система с представлением знака и величины модуля также не уникальна. Существуют некоторые системы счисления, которые используют попеременные представления для всех чисел. Одна такая система была придумана для того, чтобы ограничить знак переноса до определенного числа цифр, в то время как другая используется для того, чтобы достичь коррекции ошибок в вычислениях. Основной ущерб этих представлений в том, что числа должны быть стандартной специфической формы для некоторых арифметических операций.
Система счисления будет избыточной, если существует меньше чисел, чем комбинаций цифр. Альтернативно разные комбинации могут относиться к одному и тому же числу. Очевидно, неуникальность подразумевает избыточность. Например, двоичная система с четными цифрами, добавленные в последнюю позицию цифр, имеет уникальное представление для каждого числа, и так как половина комбинаций запрещены, это представление является избыточным.
Также десятичная система, представленная в двоичном коде, как определено следующим уравнением, является избыточной:
x = (αn323 + αn222 + αn121 + αn020)10n + …+
+ (α0323 + α0222 + α0121 + α0020)100, (2)
где αi,j или 0 или 1 и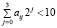 
для всех i. Избыточность проистекает из факта, что 6 из 16 двоичных комбинаций в каждой десятичной позиции не возникло.
Система счисления является позиционной, если существует набор позиций wi так, чтобы для любого числа х в системе, х может быть выражено в форме
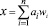, (3)
где αi – набор допустимых цифр. Если значения для wi это последовательные степени одного числа, то система счисления имеет фиксированное основание, например, основание 10 – для десятичной системы, основание 2 – для двоичной системы.
Позиционные системы счисления важны, потому что они обычно допускают подходящее сравнение величин двух чисел путем простой операции сравнения цифр в соответствующих позициях. Однако есть исключения, и не каждая позиционная система допускает определение сходного значения величины путем сравнения двух чисел. Например, рассмотрим следующую определяемую связь соотношением для системы счисления:
x = 4α2 + 3α2 + 2α1 + 2α0,
где 0 ≤ αi < 10. Должно быть ясно, что сравнение сходного значения в этом представлении требует не только поцифрового сравнения. Эта система все еще является точно распределенной.
Достаточное условие для допускаемого сравнения величин путем сравнения цифр в том, чтобы
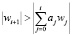(4)
для всех допустимых комбинаций αj. Система с фиксированным основанием удовлетворяет этому условию, обеспечивая αj меньшее, чем основание. Двоично-кодированная десятичная система, которая является представлением системы со смешанным основанием, тоже имеет эту характеристику. Двоично-кодированная десятичная система, как показывает уравнение (2), не подходит к категории с фиксированным основанием потому, что, например, цифра α01 имеет позицию 2, в то время как цифра α10 имеет позицию 10.
Этот тип систем широко используется в остаточных вычислениях.
Одной из непозиционных систем счисления является код Грея, который широко используется в аналого-цифровом преобразовании и пересчетных устройствах. Он позволяет существенно уменьшить время преобразования сигнала за счет упрощения кодирующей логики, что, в свою очередь, позволяет повысить эффективность защиты при переходах входного сигнала от нежелательных сбоев. Данному коду свойственна важная черта: два смежных целых числа имеют во всем идентичные представления на одну цифровую позицию. Алгоритм перехода двоичного сигнала к коду Грея можно представить в форме следующего правила: старшие разряды двоичного сигнала совпадают, а любой последующий разряд определяется суммой по модулю 2 соответствующего и предыдущего разряда кода двоичного сигнала (рис. 1).
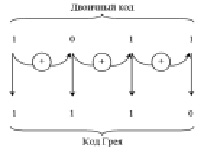
Рис. 1. Правило перевода двоичного сигнала в код Грея
Для осуществления обратного перехода от кода Грея в двоичный код, необходимо выполнить преобразование: старший разряд кода совпадает, а коды остальных разрядов сигнала равны сумме по модулю 2 полученного и текущего кода разряда двоичного сигнала (рис. 2).
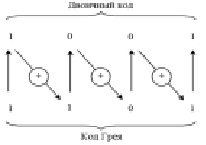
Рис. 2. Правило перевода кода Грея в двоичный код
С точки зрения алгебры логики, данные преобразования кодов двоичного сигнала представляют собой последовательные рекуррентные связи, например, если рассматривать логические выражения по преобразованию разрядов кода Грея в двоичный код, то получим следующие выражения:
, 
, 
,
,
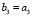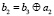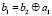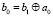т.е. в общем виде данная последовательность формул примет вид
.
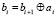Аналогично можно вывести формулу и для получения двоичного кода:
.
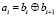Недостатком рассматриваемого кода считается тот факт, что с такого рода сигналами осложнено выполнение арифметических операций.
Из вышесказанного следует, что только две системы счисления нашли общее использование в компьютерных применениях: двоичная система и некоторое изменение двоично-кодированной десятичной системы. Обе (двоичная и десятичная) системы счисления являются позиционными системами с фиксированным основанием. Этим системам свойственны следующие важные положительные черты: простая аппаратурная реализация сравнения чисел; умножение или деление на степень 2 и 10 можно выполнить путем смещения цифр в регистры хранения; расширение пределов системы счисления легко реализуется путем добавления большего количества цифровых позиций; логика, необходимая для выполнения сложения, является идентичной для всех цифровых позиций; простота обнаружения избытка; простое преобразование из цифровой формы в аналоговую.
Признаки, которые ведут к этим положительным чертам, налагают ограничения на скорость, с которой могут быть выполнены арифметические операции, поскольку из-за распространения переноса невозможна параллельность операций. Для всех арифметических операций в этих обеих системах счисления, каждая цифра результата – это функция всех цифр равной или меньшей значимости. Эта черта делает непрактичным внедрение параллельного сложения, вычитания, умножения или деления для чисел, состоящих из нескольких цифр и, следовательно, налагает так называемое фундаментальное ограничение на скорость арифметических операций.
Существуют способы обойти скоростное ограничение, и их можно разделить на две категории: методы для уменьшения времени распространения переноса путем добавления специализированных схем переноса и использование систем счисления со специальными характеристиками переноса. Примером такой системы счисления является система остаточных классов.
В системе остаточных классов арифметические операции являются свободными от переноса, т.е. каждая цифра результата – это функция только одной цифры каждого операнда, она не зависима от всех остальных цифр оснований. За счет свойства свободного переноса осуществляется скорость операций, таких как сложение, вычитание и умножение комбинаторной логики. В частности, для случая умножения, необходимость в частичных результатах исключена.
Система остаточных классов не является позиционной системой счисления и не обладает теми положительными свойствами, перечисленными ранее и характеризующими двоичную или десятичную системы счисления, она является системой счисления целых чисел. К этому времени известные технологии делают неудобным представление дробных величин. Все операнды должны быть целыми числами, и результат арифметических операций тоже должен быть выражен целыми числами. Два важных следствия следуют из этих фактов: частные должны быть округлены до ближайшего целого значения, в большинстве вычислений, абсолютная величина результата будет больше, чем вводные значения, используемые для вычислений. Последний факт особенно важен, так как на сегодняшний день он стал одной из важных проблем, стоящих в применении модулярной арифметики. Компьютеру необходимо иметь числовые пределы значительно больше, чем пределы вводной информации, чтобы держать результат арифметики в пределах машины. Альтернативно используемые величины должны быть перемасштабированы при использовании некоторых методов деления, так как деление – это одна из сравнительно медленных операций, перемасштабирование не является подходящей операцией для выполнения. Представление в остатках является уникальным, но может быть избыточным и безызбыточным в зависимости от желаемого применения.
Так как модулярные системы предлагают несколько интересных альтернатив, можно принимать во внимание эффект замены традиционной системы на систему остаточных классов. Как выделялось ранее, настоящее использование систем счисления с фиксированным основанием в компьютерах, как правило, имеет ряд отрицательных черт. Умножение и деление более сложны для выполнения, чем сложение и вычитание. Более того, сложение, которое само по себе является основной операцией и которое также используется в выполнении умножения, не всегда легко выполнить, так как каждая цифра суммы – это функция всех менее значительных цифр операндов. Хотя это свойство может не являться отрицательной чертой в вычислениях вручную или серийных вычислениях, в параллельной обработке подразумевается либо удлиненное время выполнения, либо необходимость в большом количестве оборудования.
С другой стороны, система остаточных классов предлагает прямые преимущества в выполнении сложения и умножения. Свойство свободного от переноса, которое является результатом относительной независимости различных цифр в остаточном числе, дает два преимущества. Первое: цифры числа можно обработать одновременно, предлагая действительно параллельные операции на все цифры. Второе: логика, необходимая для того, чтобы обработать каждую цифру, является независимой от других цифр так, что число комбинаций и, следовательно, сложность логики значительно уменьшаются.
Чтобы показать преимущества арифметических операций СОК, рассмотрим N-бит, двоичную систему с фиксированным основанием. Например, рассмотрим числа 12 и 15, которые в двоичной системе представляются соответственно 1100 и 1111. Получили 4-битовое представление сигналов.
Комбинаторная логика для выполнения таблицы истинности для умножения имела бы 22N элементов, где каждый элемент состоит из 2N бит. Действительно, для рассматриваемого примера результат арифметической операции умножения кодов 1100 и 1111 равен 10110100, т.е. получили 8-битовый код.
Эквивалентное остаточное число состояло бы из нескольких остаточных цифр, каждая – кодированная двоичными цифрами. Общее число битов в слове превышало бы N-бит традиционного двоичного числа не более 20 %. Например, предположим, что базис СОК с основаниями {2, 3, 5, 7}, тогда динамический диапазон для данной системы определяется соотношением
.
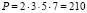Тогда рассматриваемые выше числа примут вид
, 
.
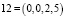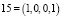Если каждое число перевести в двоичную систему, то получим:
, 
.
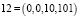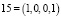Тогда произведение полученных кодов имеет вид
,
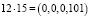т.е. вычисления во втором случае оказываются проще.
Так как каждая остаточная цифра суммы или произведения – это функция только соответствующей остаточной цифры, каждая остаточная цифра имела свою собственную независимую таблицу или логические схемы. В примере рассмотрено 4 основания, но если мы предположим 10 оснований, то комбинации, необходимые для каждой остаточной цифры, порядка 
; общее для всего остаточного числа порядка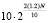 
, каждое определяется только N/10 бит. Сложность результата значительно меньше, чем для традиционной двоичной системы.
Подвергается серьезному вопросу основной результат, описанный в предыдущем обсуждении, т.к. он основан на грубых и, возможно, сомнительных предложениях. Тем не менее, пример иллюстрирует одну из основных мнений аргумента, который придает поддержку серьезным исследованиям системы остаточных классов. Система остаточных классов требует значительного изучения в деталях так, чтобы более значимые заключения, касающиеся пользы системы, можно было бы применить.