Повышение качества и надежности выпускаемых изделий приборо- и машиностроения обеспечивается в числе прочего механическими испытаниями на вибрационную нагрузку, которые выполняются как для разрабатываемых новых изделий, так и для серийных образцов. При вибрационных испытаниях объектов, имеющих большую массу, требуется достаточно мощный силовой привод, в качестве которого в виброиспытательных стендах часто используется электрогидравлический следящий привод (ЭГСП), отличающийся высокой удельной мощностью и быстродействием [1], [4]. При испытаниях на случайную вибрационную нагрузку необходимо получить на выходе виброиспытательного стенда испытательное воздействие (перемещение рабочего стола или платформы стенда с закрепленным изделием) в виде случайного процесса с требуемой корреляционной функцией и математическим ожиданием. Однако ввиду нестабильности параметров ЭГСП, обусловленных как внешними (температура окружающей среды), так и внутренними (технологический разброс значений параметров, содержание газовой фазы в рабочей жидкости) случайными факторами, имеет место искажение упомянутых статистических характеристик формируемого вибрационного воздействия. Например, если на вход виброиспытательного стенда подается аддитивная смесь детерминированного и случайного сигналов, то случайность параметров виброиспытательного стенда приводит к существенным колебаниям дисперсии формируемого случайного вибрационного воздействия, вызванным колебаниями детерминированной составляющей входного сигнала. Это является одной из особенностей стохастических систем, состоящей в том, что корреляционная функция, а значит, и дисперсия выходного сигнала системы со случайными параметрами определяется не только корреляционной функцией входного сигнала, как это имеет место для детерминированной системы, но и математическим ожиданием данного сигнала. Таким образом, указанные колебания дисперсии выходного сигнала ЭГСП, искажающие характеристики вибрационного воздействия, могут привести к снижению качества вибрационных испытаний и получению неадекватных результатов в случаях, когда требуется обеспечить точное соответствие формируемых вибрационных воздействий некоторым реальным. Следовательно, задача компенсации фактора случайности параметров ЭГСП является актуальной.
Целью настоящей работы является определение способа компенсации фактора случайности параметров ЭГСП в составе виброиспытательного стенда, на вход которого поступает сумма случайного и детерминированного сигналов, обозначаемых далее как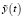 
и 
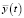. При этом случайный сигнал представляет собой центрированный гауссов случайный процесс с заданным законом изменения дисперсии, в частном случае – стационарный случайный процесс, а детерминированный – гармонический сигнал, формирующий математическое ожидание суммарного входного сигнала. Это соответствует таким основным видам возбуждаемой вибрации, как синусоидальная вибрация на фиксированных либо переменных частотах и широкополосная случайная вибрация.
Компенсация фактора случайности параметров
Для компенсации фактора случайности параметров ЭГСП предлагается использовать подход, состоящий в формировании такого случайного входного сигнала, который обеспечил бы устранение указанного влияния детерминированной составляющей (математического ожидания) входного сигнала за счет соответствующей модуляции амплитуды его случайной составляющей. В терминах теории управления такой подход соответствует задаче синтеза программных управлений в статистической постановке и относится к классу обратных задач динамики [3]. Далее рассмотрим алгоритм синтеза программного управления механическими колебаниями штока гидроцилиндра ЭГСП при формировании случайного вибрационного воздействия, основанный на использовании усредненной проекционной модели и процедуры оптимизации квадратичного функционала.
Математическая модель ЭГСП в линейном приближении описывается следующим дифференциальным уравнением:
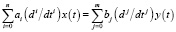, (1)
где y(t) – входной сигнал (электрическое напряжение), x(t) – выходной сигнал (перемещение штока поршня).
Коэффициенты уравнения (1) функционально зависят от случайных физических параметров ЭГСП, которые могут являться либо случайными величинами, либо случайными процессами. Таким образом, модель (1) соответствует стохастической системе. Для пояснения вышеупомянутой идеи компенсации фактора случайности параметров ЭГСП рассмотрим усредненную проекционную модель, полученную в результате проекционной аппроксимации исходной модели (1). Процедура построения таких моделей для систем со случайными параметрами с использованием методов теории матричных операторов [2] подробно описана в [5]. Усредненная проекционная модель устанавливает связь между статистическими характеристиками входного и выходного сигналов и для данного класса стохастических систем имеет следующий вид:
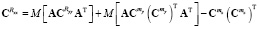, (2)
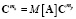, (3)
где A – квадратная матрица проекционной характеристики (матричный оператор) системы;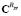 
и 
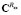– квадратные матрицы проекционных характеристик корреляционных функций входного и выходного сигналов; 
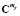и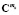 
– вектор-столбцы проекционных характеристик функций математических ожиданий выходного и входного сигналов; 
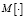– оператор математического ожидания; T – знак транспонирования.
Проекционные характеристики корреляционных функций и функций математических ожиданий представляют собой соответственно матрицы или вектор-столбцы коэффициентов разложения этих функций времени по некоторому ортогональному базису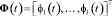 
. При этом связь между приближенными представлениями указанных функций и их проекционными характеристиками для базиса размерности l выражается следующим образом:
,
,
.
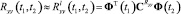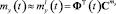
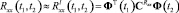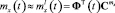Проекционная характеристика системы A строится с использованием матричных операторов интегрирования [2]. В выражение для нее входят коэффициенты уравнения (1), поэтому матрица A является случайной. Операция усреднения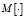 
реализуется с использованием приема разложения стохастического оператора A в матричный ряд с последующим аналитическим усреднением членов этого ряда [5]. Аналитическое усреднение состоит в выражении стохастических моментов (порядка выше второго) случайных коэффициентов исходного уравнения модели (1) через дисперсии и математические ожидания этих коэффициентов для каждого члена упомянутого ряда.
Операторная форма записи решений, характерная для проекционных методов, позволяет предложить следующий подход к компенсации фактора случайности параметров ЭГСП на основе анализа выражения (2). Из данного выражения видно, что влияние ненулевого математического ожидания входного сигнала обусловлено вторым и третьим слагаемым в его правой части. Идея компенсации этого влияния состоит во введении матрицы умножителя на некоторую корректирующую функцию f(t) (матричный оператор умножения Af) в первое слагаемое, то есть в преобразовании (2) к виду
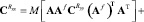
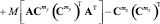, (4)
что соответствует введению умножителя в цепь центрированной случайной составляющей входного сигнала системы. Далее скорректированная случайная и детерминированная составляющие поступают на вход сумматора, формирующего смешанный входной сигнал y(t).
Уменьшение среднего уровня дисперсии выходного сигнала системы, обусловленное действием умножителя Af, компенсируется добавлением к входному сигналу второй случайной составляющей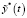 
в виде центрированного случайного процесса, некоррелированного с первой случайной составляющей 
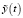и имеющего корреляционную функцию того же вида, но с дополнительным коэффициентом k. Например, если корреляционная функция случайной составляющей входного сигнала имеет вид 
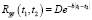, то корреляционная функция второй случайной составляющей 
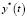будет определяться как
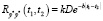. (5)
Тогда выражение (4) будет иметь вид
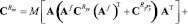
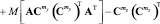, (6)
а сигнал на входе ЭГСП будет формироваться следующим образом:
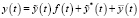. (7)
Если детерминированная составляющая является гармоническим сигналом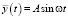 
, то функция f(t) может выглядеть так:
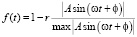, (8)
где коэффициент r определяет уровень компенсации, а ? – фазовый сдвиг, позволяющий получить «противофазный» сигнал f(t), гасящий колебания дисперсии выходного сигнала системы.
Для нахождения параметров r, ? и k воспользуемся приемом минимизации следующего функционала, выражающего близость корреляционных функций выходного сигнала стохастической системы (1) и детерминированной системы, также описываемой уравнением (1), в котором все случайные коэффициенты заменены своими математическими ожиданиями:
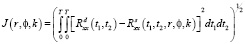, (9)
где 
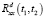и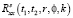 
– корреляционные функции выходного сигнала детерминированной и стохастической системы соответственно, при этом последняя зависит от искомых параметров компенсации.
Проекционная аппроксимация модели (1) позволяет представить функционал (9) в следующей удобной для вычисления форме:
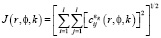, (10)
где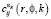 
– элементы квадратной матрицы, вычисляемой как
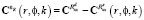, (11)
где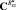 
и 
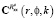– проекционные характеристики корреляционных функци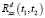й 
и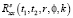 
соответственно.
Проекционная характеристика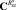 
(r, ?, k) в (11) вычисляется по усредненной проекционной модели системы (1).
Пример компенсации случайности параметров электрогидравлического привода
В качестве примера решения задачи компенсации влияния случайности параметров ЭГСП, описываемого моделью (1), где n = 5 и m = 0, построенной на основе типовой модели ЭГСП [4], на дисперсию его выходного сигнала, рассмотрим отработку детерминированного сигнала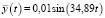 
с наложенной на него центрированной случайной составляющей 
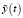с корреляционной функцией 
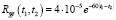. В качестве случайного параметра возьмем коэффициент вязкого трения на золотнике электрогидравлического усилителя, обозначив его как hЗ. Данный параметр будем считать гауссовой случайной величиной с математическим ожиданием 
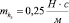и дисперсией 
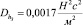. При этом в уравнении (1) случайными будут коэффициенты а1, а2, а3, а4, математические ожидания и дисперсии которых вычисляются через заданные 
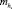и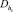 
. В качестве ортогонального базиса Ф(t) будем использовать базис функций Уолша с l = 64.
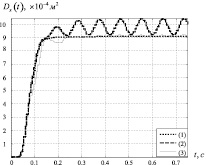
Рис. 1. Дисперсия выходного сигнала ЭГСП: 1 – для детерминированной модели; 2 – для стохастической модели без компенсации влияния случайности параметра; 3 – для стохастической модели c компенсацией влияния случайности параметра
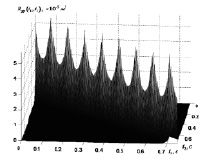
Рис. 2. Корреляционная функция входного сигнала ЭГСП
Выполняя минимизацию функционала (10) методом Нелдера-Мида при начальных значениях r = 0,5, ? = 0,3, k = 0,5, находим следующие оптимальные значения параметров компенсации: r = 0,5267, ? = 0,2213, k = 0,4664.
На рис. 1 представлены графики дисперсии выходного сигнала ЭГСП x(t) до и после компенсации влияния случайности параметра hЗ.
На рис. 2 приводится график корреляционной функции скорректированного входного сигнала y(t), формируемого согласно (7).
Заключение
Предложенный способ компенсации случайности параметров электрогидравлического привода виброиспытательного стенда позволяет построить эффективный алгоритм формирования его входного сигнала, который обеспечивает практически полное гашение колебаний дисперсии формируемого вибрационного воздействия, обусловленных влиянием случайности параметров электрогидравлического привода при отработке случайного входного сигнала, содержащего детерминированную составляющую. Матрично-операторная форма записи решений, характерная для проекционных методов, дает возможность построить удобный для вычисления функционал, минимизация которого обеспечивает нахождение оптимальных параметров компенсации. Возможность практического применения предложенного алгоритма показана на примере компенсации случайности одного из параметров типовой математической модели электрогидравлического следящего привода.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований и Правительства Калужской области (грант № 14-41-03071).