Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Страховые резервы – важный компонент финансовой устойчивости страховых организаций. Они необходимы для обеспечения будущих выплат и, следовательно, для достижения баланса текущих и будущих денежных потоков. Поэтому их прогнозирование является важной актуарной задачей.

В частности, резервы произошедших, но незаявленных убытков (РПНУ) представляют собой финансовые средства для страхового возмещения по тем страховым случаям, про которые страховая организация ещё не проинформирована страхователями или проинформирована не полностью. Подобные задержки в информировании связаны с особенностями процессов возникновения застрахованного ущерба в страховании ином, чем страхование жизни, и его документального подтверждения. В зависимости от вида страхования они могут достигать нескольких месяцев или даже лет.

Иными словами, имеется существенная потребность в прогнозировании будущих страховых выплат в динамике, с разбивкой по группам страховых договоров. Для её удовлетворения разработан ряд методов, широко используемых актуариями (Norberg, 1993; Taylor, 2000; Wüthrich, Merz, 2008). Их суть состоит в том, что выделяются группы относительно однородных договоров (со схожими характеристиками риска), заключённых в одни и те же периоды. Далее, на основе предположения о том, что развитие убытков в соответствующих группах подчиняется схожим закономерностям, составляется треугольник наблюдаемых выплат, на основе которого происходит прогнозирование нижнего треугольника будущих выплат (рис. 1).

Все периоды одинаковы, их выбирают в различных методиках из разных соображений (год, квартал и т.п.). На дату оценки резерва для разных групп договоров достигаются различные периоды урегулирования. На рис. 1 цветом выделены ячейки, соответствующие заявленным убыткам по прошлым календарным периодам, а белый цвет показывает ячейки, для которых нужно спрогнозировать величину выплат. Данные, расположенные на диагонали (в последних цветных ячейках каждой строки), отвечают за выплаты за период, предшествующий отчётной дате. Размерность подобной таблицы может быть выбрана из разных соображений. Часто размерность завышают с тем, чтобы урегулирование в течение этого периода произошло гарантированно (скажем, 3, 5 или 7 лет). Но возможен такой выбор, что таблица отражает существенные выплаты, а «хвост», выпадающий за эту границу, оценивают отдельно (Сихов и др., 2013).

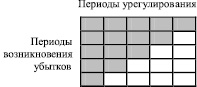
Рис. 1. Пояснение методов треугольника

Хотя методы прогнозирования, построенные по описанной схеме, довольно сильно развиты и достаточно широко распространены, имеется проблема точности прогнозирования. Дело в том, что каждый метод основан на своей системе предпосылок (предположений и гипотез) о будущем развитии страховых убытков. Эти гипотезы не всегда можно проверить на реальных данных как из-за их ограниченности (например, для новых видов страхования), так и в связи со специфическим «треугольным» представлением, при котором часть информации теряется вследствие агрегации. Тем не менее оценки резерва непосредственно включаются в финансовую отчётность, так что любые ошибки при прогнозировании превращаются в искажения финансовых показателей. Иными словами, техническая проблема актуарного оценивания превращается в проблему финансового менеджмента, а точность оценивания резервов является ключевым аспектом управления страховой организацией и эффективности страхового надзора.

Сложность состоит в том, что контролировать точность оценивания напрямую практически невозможно из-за большого многообразия особенностей видов страхования, структуры страховых портфелей и ряда других факторов. В частности, попытки нормативного установления метода оценки резервов произошедших, но незаявленных убытков неэффективны из-за возможного несоответствия предпосылок метода особенностям оцениваемого вида страхования.

Одним из способов контроля точности оценок является ретроспективное сравнение таких оценок с фактическими выплатами. Конечно, такой подход не позволяет оперативно вносить поправки в актуарные оценки, но он позволяет прояснить правильность выбора предпосылок и метода оценивания, что уменьшает степень субъективности для последующих оценок.

Обычно предлагается сравнивать оценки резерва с фактическими выплатами по соответствующим периодам. Так, в стандарте Гильдии актуариев «Актуарный стандарт № 1 “О формировании страховых резервов по видам страхования иным, чем страхование жизни”» (Стандарт, 2014) предлагается проводить сравнение на ежегодной основе с глубиной горизонта в несколько лет.

При таком подходе оценка точности по такой методике будет получена уже после полного урегулирования, когда большая задержка в получении информации сделает её практически бессмысленной. Полезность методики состоит только в том, что увязка выявленных отклонений с особенностями расчётов поможет уточнить предпосылки по текущим расчётам (правда, без гарантии их адекватности). В этой связи встаёт вопрос о более быстром получении информации о возможном несоответствии прогноза фактическим выплатам, который позволил бы вносить поправки в оценки для ещё неурегулированных групп рисков.

Описание предлагаемого метода

Для сравнения прогнозных значений с фактическими выплатами не требуется ждать несколько лет. Данные и так уже разделены по периодам, так что точность оценки можно узнавать поэтапно, в отношении отдельных групп данных. С учётом дополнительных поправок, отражающих объём данных и иные факторы, эту частичную оценку можно переносить на весь резерв, что позволяет оперативно пересматривать методику и предпосылки оценки.

Для построения методики сравнения достаточно заметить, что пересчёт резерва происходит периодически, для каждой отчётной даты. Это означает сдвиг соответствующих ячеек вниз на подходящее число строк. В результате последовательные оценки используют частично те же данные, частично – новые. Это позволяет сопоставлять оценки в разные периоды времени. Подробнее типичное соотношение используемых данных показано на рис. 2.

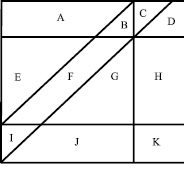
Рис. 2. Типичная схема данных для метода треугольника

На данной схеме не указаны отдельные ячейки, отвечающие периодам: схема отражает процесс для индивидуальных данных. Группировка по периодам не изменит структуры данных. Левая вертикальная линия отражает момент возникновения убытков, а правая вертикальная линия – горизонт наблюдения, т.е. всё, что справа от неё, – «хвост» урегулирования, который может оцениваться отдельно. Если границы областей выбирают так, что максимальный срок урегулирования заведомо укладывается в рассматриваемый треугольник, то выплаты для областей C, D, H и K отсутствуют. Между первой и третьей горизонтальной линией находится статистика и прогнозы для договоров страхования, по которым страховые случаи произошли до отчётной даты 0. Между третьей и четвёртой горизонтальной линией находится статистика и прогнозы для договоров, по которым страховые случаи произошли между отчётными датами 0 и 1. При оценке резервов в отчётную дату 1 на практике часто отбрасывают информацию по аналогичному числу периодов, использованных для предыдущей оценки (полоса между первой и второй горизонтальными линиями). Наклонные линии отделяют наблюдаемые значения от прогнозируемых для разных сроков оценки.

В момент времени 0 по наблюдаемым данным о заявленных и/или оплаченных убытках A и E оценивается резерв

R0 = B0 + C0 + D0 + F0 + G0 + H0,

который представляет собой прогноз будущих выплат. Соответственно индекс «0» в обозначениях указывает на момент оценки. За период между отчётными датами 0 и 1 становятся известны фактические убытки B, C, F и I, так что в момент времени 1 по наблюдениям

A + B + C + E + F + I

оценивается резерв

R1 = D1 + G1 + H1 + J1 + K1.

Если убытки D1 не ожидаются или не существенны, то наблюдения A + B + C на практике игнорируются, так что оценки R0 и R1 происходят фактически по одной и той же схеме. Тем не менее даже в этом случае могут иметь место расхождения из-за различий в предпосылках или изменении метода оценивания. Последние могут объясняться, например, уточнением представлений актуария о процессе развития убытков и расширением объёма наблюдаемой статистики.

Прирост (изменение) резерва, также являющейся важным элементом финансовой отчётности, составит величину

ΔR = R1 – R0 = –B0 – C0 + + ΔD – F0 + ΔG + ΔH + J1 + K1,

где ΔD = D1 – D0; ΔG = G1 – G0; ΔH = H1 – H0 – соответствующие изменения будущих оценок вследствие различий в предпосылках и смене метода оценки. Если существенных изменений во взглядах на оценивание будущих убытков вида D, G и H не произошло, то ΔD = ΔG = ΔH = 0. В противном случае они могут довольно серьёзно повлиять на финансовую отчётность. Именно поэтому в ней должны содержаться комментарии по поводу методов актуарного оценивания, а сами величины ΔD, ΔG и ΔH должны внимательно анализироваться при переходе от оценок одного периода к оценкам другого периода.

Тем не менее этого не достаточно для характеристики точности оценивания, так как необходимо сопоставить актуарные оценки будущих выплат, сделанные ранее, с фактическими убытками. Если ставшие известными за период между моментами времени 0 и 1 убытки B + C + F + I сложить с приростом резерва ΔR, то получим величину

δB + δC + ΔD + δF + ΔG + ΔH + I + J1 + K1,

где δB = B – B0, δC = C – C0, δF = F – F0 – соответствующие ошибки оценивания в момент времени 0. В идеальном случае, когда актуарию удалось полностью предсказать размер будущих выплат, они равны нулю. На практике почти всегда будут наблюдаться отклонения, которые можно считать допустимыми, если они укладываются в соответствующий доверительный интервал.

При этом I + J1 + K1 представляет собой величину ожидаемых выплат по соответствующим группам, которые нужно учитывать в момент времени 1, где I – фактический ущерб, который был заявлен или оплачен, а J1 + K1 – соответствующие оценки будущих выплат. Исключив эту величину, получим значение

δB + δC + ΔD + δF + ΔG + ΔH,

характеризующее точность оценивания резерва произошедших, но незаявленных убытков. Она распадается на две части (1) δB + δC + δF, отражающую выявленные за период между моментами времени 0 и 1 отклонения фактического ущерба от его оценки в момент 0, и (2) ΔD + ΔG + ΔH, которая описывает изменения в оценках, сделанных на отчётную дату 0 и 1 соответственно. Если границы областей выбирают так, что максимальный срок урегулирования заведомо укладывается в рассматриваемый треугольник (выплаты для областей C, D, H и K отсутствуют), то первая компонента, отвечающая за точность предыдущей оценки, равна δB + δF, а вторая компонента, связанная с переоценкой резерва, равна ΔG. Величину δB нужно рассматривать даже если данные типа A игнорируются при оценке резерва в момент времени 1, так как здесь измеряется именно точность резерва, оцененного на предыдущую дату, где эти данные были важны.

Причины отклонения от нуля указанных компонент различны, поэтому их необходимо анализировать отдельно друг от друга, хотя как сами эти компоненты, так и суммарное значение имеет смысл сравнивать с величиной резерва (в момент 1). Особое внимание при практическом анализе следует уделять случаям, когда соответствующие относительные значения велики. Вторая компонента рассматриваемой статистики изменения резервов (ΔD + ΔG + ΔH) так же, как и первая (δB + δC + δF), содержит ошибки оценивания, связанные с отклонением от будущих фактических значений. Поэтому подобный анализ необходимо проводить ретроспективно, чтобы выяснить, уменьшали ли новые оценки резерва ошибки оценивания или нет.

Иллюстративный пример

Для пояснения приведённого анализа рассмотрим пример, основанный на реальных данных одной из крупных страховых компаний Казахстана. Взяты оценки резерва по страхованию автомобилей (каско). Данные взяты с января 2012 года по июнь 2015 года включительно, что позволяет рассчитать оценку РПНУ на две отчётные даты – 31 декабря 2014 года (момент времени 0) и 30 июня 2015 года (момент времени 1) с горизонтом глубиной 3 года (12 кварталов). В обоих случаях расчёты проводились методом цепной лестницы (сам метод и базовые предпосылки не менялись). Длина единичного периода ? один квартал. Все величины пересчитаны в тыс. российских рублей. Результаты сравнения согласно методу, изложенному в предыдущем пункте, приведены в табл. 1.

Таблица 1

Сравнение точности оценок РПНУ

Отклонение составило достаточно большую величину, составляющую 9,6 % от резерва на 31 декабря 2014 года. Тем не менее оно почти полностью объясняется изменениями в оценке. Хотя метод и предпосылки не пересматривались, имел место пересмотр выплат вследствие суброгации и регрессов, а также поступлений имущества и (или) его годных остатков. Кроме того, метод цепной лестницы довольно чувствителен к большим выплатам, которые осуществляются со значительной задержкой: такие эффекты имели место в первой половине 2012 года (соответственно это повлияло на оценку в момент времени 0, но не имело значения в момент времени 1), а также в первой половине 2015 года (обратный эффект). В результате оценки коэффициентов развития убытков изменились, что привело к снижению резерва.

В табл. 2 приведена детализированная информация об изменении статистики. В таблице отсутствуют ячейки, относящиеся к областям C, D, H и K, так как максимальный срок урегулирования взят с избытком. В ней также убраны строки, соответствующие областям A и B, необходимые только для резерва на 31 декабря, и областям I и J, отвечающие за убытки, возникшие в первой половине 2015 года. Очевидно, для них проблема сопоставления не стоит (для указанных отчётных дат).

Таблица 2

Отклонения оценок

Строки соответствуют кварталам возникновения убытков (наступления страховых случаев). Столбцы отвечают за задержку в урегулировании (например, первый столбец отражает убытки, урегулированные в том же квартале, когда они возникли, т.е. задержка равна нулю). Данные разделены жирной линией на три области. Верхняя область показывает изменения статистики прошлых выплат вследствие суброгации и регрессов. Эти данные в нашей оценке не участвовали, но именно эти изменения частично ответственны за снижение размера резерва на 30 июня 2015 года. Средняя область между линиями содержит информацию об отклонениях фактических выплат, произведённых в первой половине 2015 года, от соответствующих прогнозных величин. Наконец, третья (нижняя) область отражает изменения оценок будущего ущерба в разные моменты времени.

Из изучения табл. 2 видно, что суброгация и регрессы прямого существенного влияния не имели, хотя их косвенное влияние (через изменение технических коэффициентов при расчётах) было значительным. Отклонения фактических выплат от прогноза также значительны, особенно по страховым случаям, произошедшим в 2014 году, что легко объяснимо небольшим объёмом доступной по ним информации. Тем не менее актуария интересуют не отдельные отклонения, а совокупные, которые весьма малы (0,8 % от резерва на 31 декабря). Поэтому данную оценку можно считать очень точной. Отклонения различных прогнозов достаточно велики, особенно для тех столбцов, где имело место искажение вследствие крупных выплат. Именно за счёт этого эффекта получается значительное совокупное отклонение (9,6 % от резерва на 31 декабря). Именно этот эффект и является причиной пересмотра величины резерва в середине года.

Выводы

Оценка точности величины страховых резервов (особенно РПНУ) представляется важной и актуальной проблемой, которая пока полностью не решена. Подход, рекомендованный актуарными стандартами, представляется неудачным. Предлагаемый в статье подход позволяет детально анализировать динамику оценок резервов, выявляя основные факторы, приводящие к изменениям. В иллюстративном примере, основанном на реальных данных, показано, что кажущаяся неточной оценка на самом деле довольно точна, а отклонения связаны с недостатками выбранного метода цепной лестницы, который чувствителен к некоторым особенностям статистических данных.

Работа выполнена при поддержке грантового финансирования научно-технических программ и проектов Комитетом науки МОН РК, грант 5024/ГФ4.