Процессы, протекающие в экономике, таковы, что постоянно изменяются различные показатели деятельности предприятий, спроса, предложения, качества жизни и т.п. В связи с этим возникает задача выбора между удовлетворением текущего потребительского спроса и обеспечением будущего спроса. Капитальные вложения в производство должны быть такими, чтобы объем производства увеличивался наиболее оптимально. Такое увеличение объема зависит от ограничений, возникающих вследствие технических особенностей процесса производства, от ценовой стабильности, полной занятости рабочей силы и прочих экономических характеристик. Таким образом, возникает необходимость выбора такого состояния экономики из возможных, которое обеспечит наиболее долгосрочную и устойчивую перспективу развития. Такая задача выбора называется задачей определения положения равновесия в экономике.
При описании задачи нахождения положения равновесия чаще всего [1–4, 6] главной задачей считается определение таких условий и параметров экономической системы, при которых это равновесное состояние достижимо. Одновременно с этим приходится учитывать ограничения на технологические множества, описывающие интенсивность производства [7, 8].
В данной работе продолжаются исследования, начатые в [7, 8]. Рассматривается технологическое множество, представленное в виде выпуклого конуса. Делается попытка изучить влияние ограничений интенсивностей производственных отраслей на векторы цен. В более ранних исследованиях [7, 8] этот момент не изучался. В данной работе ограничения на векторы цен устанавливаются в виде конуса, сопряженного к конусу, в котором лежат векторы интенсивностей производственных процессов.
Кроме того, в статье оценивается положение равновесия в случаях, когда матрица модели представляет собой интервальную матрицу [5]. Вполне логично, что при нечетких начальных данных параметры модели могут существенно изменяться. Для оценки положения равновесия модели в этом случае осуществляется переход к оптимизационным задачам.
Постановка задачи и решение
Будем рассматривать модель Леонтьева, определяемую технологической матрицей A = (aij) [2, 7]. Предположим, что число базисных процессов равно числу товаров, т.е. матрица A является квадратной матрицей размерности n×n; более того, пусть A ≥ 0 – неразложима и примитивна.
Обозначим через z = (z1, ..., zn) – вектор интенсивностей базисных процессов, а через p = (p1, ..., pn) – соответствующий вектор цен. Говорят [2], что модель Леонтьева находится в состоянии динамического равновесия, если выполнены условия
z(E – γA) ≥ 0; (E – γA)pT ≤ 0;
z(E – γA)pT = 0, (1)
где E – единичная матрица, а γ – положительное число.
Предположим, что в связи с технологической реализуемостью в рассматриваемой экономике возникают ограничения на векторы интенсивности. Будем считать, что эти векторы z принадлежат не всему 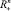 , как обычно [6], а некоторому подмножеству
, как обычно [6], а некоторому подмножеству 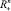 множеству Tz, которое является выпуклым многогранным конусом.
множеству Tz, которое является выпуклым многогранным конусом.
Пусть [4], 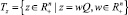 с некоторой квадратной матрицей Qn×n, причем qij ≥ 0, и матрицы A и Q коммутативны. Пусть матрица Q имеет обратную матрицу Q–1. Обозначим через Tp конус, определяемый соотношением
с некоторой квадратной матрицей Qn×n, причем qij ≥ 0, и матрицы A и Q коммутативны. Пусть матрица Q имеет обратную матрицу Q–1. Обозначим через Tp конус, определяемый соотношением 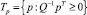 . Имеет место
. Имеет место
Теорема 1
Пусть в неотрицательной матрице A нет нулевых строк. Тогда существует решение системы (1) z ∈ Tz, p ∈ Tp.
Доказательство. При доказательстве существования равновесия принципиальным является переход от неравенства z(E – γA) ≥ 0, z ∈ Tz к неравенству (E – γA)pT ≤ 0, p ∈ Tp [2]. Опишем этот переход подробно.
Обозначим λ = 1/γ. Тогда неравенства
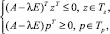 (2)
(2)
при подстановке z = wQ равносильны неравенствам
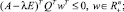
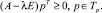
Тогда
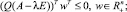
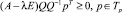
или
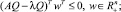
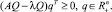
Таким образом, неравенства (2) эквивалентны неравенствам
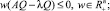
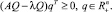 (3)
(3)
Система неравенств (3) соответствует модели Неймана (AQ, Q) и, значит [2], имеет решение. Так как эта система эквивалентна системе (2), то и система (2) имеет решение. Справедливость третьего соотношения в (1) устанавливается аналогично.
Теорема доказана.
Общим положением равновесия модели Леонтьева с производственной матрицей A и матрицей ограничений Q назовем решение (λ, z, p) системы (2), соответствующее решению системы (3).
Для исследования модели важны частные положения равновесия с соответствующими экстремальными значениями λ, которые можно найти, перейдя к следующим оптимизационным задачам [1]:
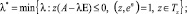 (4)
(4)
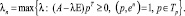 (5)
(5)
Числа λn и λ* называются числами Неймана и Фробениуса и определяют максимальный и минимальный темп равновесного роста модели соответственно.
Примем во внимание два обстоятельства. Во-первых, все элементы матрицы Q неотрицательны (qij ≥ 0). Во-вторых, векторы w и q принадлежат симплексам, что является следствием однородности задачи. При введении в систему матрицы Q однородность сохраняется, поэтому по-прежнему можно считать, что (z, en) = 1, z ∈ Tz, и (p, en) = 1, p ∈ Tp. Здесь en = (ei)T, ei = 1, i = 1...n – единичный вектор размерности n. Тогда из (4) и (5) следует, что для нахождения параметров продуктивности модели и ее положения равновесия следует решить оптимизационную задачу вида [5]:
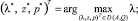 (6)
(6)
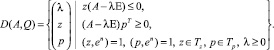 (7)
(7)
Интересно отметить, что в указанном случае возможны некоторые оценки положения равновесия для интервальных моделей леонтьевского типа.
Интервальные модели
Обозначим 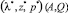 – параметры равновесия модели Леонтьева, задаваемой матрицей A с матрицей ограничений Q, соответствующего системе (2).
– параметры равновесия модели Леонтьева, задаваемой матрицей A с матрицей ограничений Q, соответствующего системе (2).
Интервальной назовем модель Леонтьева (2) с матрицей затрат 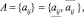
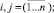
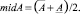
Здесь midA – матрица центров интервалов матрицы A; 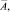
 – матрицы точных верхних и нижних граней соответственно [5].
– матрицы точных верхних и нижних граней соответственно [5].
Теорема 2
Пусть интервальная модель Леонтьева с матрицей затрат A и ограничением на вектор производства в виде выпуклого конуса с матрицей Qn×n задана интервальной матрицей A. Пусть также для точечной матрицы 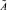 выполнены условия:
выполнены условия:  ,
,
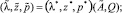 (8)
(8)
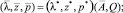 (9)
(9)
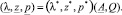 (10)
(10)
Тогда 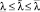 .
.
Доказательство. Точечная матрица представима в виде
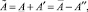
где 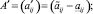
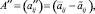 причем элементы матриц A′ и A″ неотрицательны. Подставив
причем элементы матриц A′ и A″ неотрицательны. Подставив 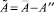 в (8), получим
в (8), получим
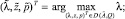
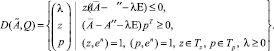
Так как матрица A″ неотрицательна, 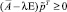 . Таким образом, ∀j = 1, 2, ... n выполняется:
. Таким образом, ∀j = 1, 2, ... n выполняется:
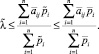 (11)
(11)
Последнее неравенство следует из условия (9) теоремы, смысл которого
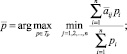
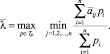
Отсюда 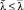 .
.
Неравенство 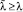 доказывается аналогично. Действительно, при подстановке
доказывается аналогично. Действительно, при подстановке 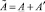 в (8) получим
в (8) получим
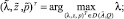
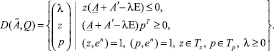
Так как матрица A′ неотрицательна, из первого неравенства следует 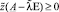 , поэтому для ∀i = 1, 2, ..., n выполняется:
, поэтому для ∀i = 1, 2, ..., n выполняется:
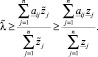 (12)
(12)
Последнее неравенство следует из условия (10) теоремы, смысл которого
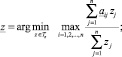
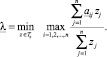
Отсюда 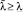 . Теорема доказана.
. Теорема доказана.
Эта теорема показывает, что для модели Леонтьева с интервальной матрицей затрат A и матрицей ограничений Qn×n число Фробениуса лежит в интервале 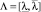 , где
, где 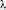 – число Фробениуса для модели с матрицей
– число Фробениуса для модели с матрицей  , а
, а  – для модели с матрицей
– для модели с матрицей 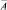 .
.
Теорема 3
Если в модели Леонтьева с интервальной матрицей затрат A и ограничением на вектор производства в виде выпуклого конуса с матрицей Qn×n точечная матрица 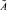 удовлетворяет условию
удовлетворяет условию 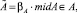 то
то 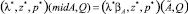 .
.
Доказательство теоремы проводится аналогично [5].
Выводы
Модели экономики леонтьевского типа, описанные выше, являются естественным обобщением модели Леонтьева: обобщение заключается в том, что допускаются ограничения на интенсивности базовых производственных отраслей, причем множество ограничений описывается в виде выпуклого конуса. Описывается переход к оптимизационным задачам, позволяющим также получить некоторые оценки положения равновесия в интервальных моделях.



