В последнее время расширяется практика разработки методов и моделей оценки проектов в реальном секторе экономики. Она преследует цель заинтересовать потенциальных участников проекта, показать, что участие в проекте будет им выгодно. Поэтому основой проектного анализа является оценка эффективности инвестиционного проекта и выбор, при наличии альтернатив, лучшего из них. При этом оценка эффективности при значительных затратах («большой проект») не может использовать традиционные методы с использованием NPV.
Оценка эффективности проекта сводится по существу к построению и исследованию некоторой экономико-математической модели процесса реализации проекта.
При оценке эффективности проектов с помощью моделей деятельности предприятия возникает ряд проблемных вопросов. В частности, в моделях одновременного инвестиционного и финансового планирования производственную сферу предприятий принимают как заданную, при этом считаются известными денежные потоки для отдельных инвестиционных проектов и с учетом предположения, что инвестиционные проекты не зависят друг от друга. Проблема заключается в том, что денежные потоки инвестиций становятся известны лишь после того, когда сформирована программа, выходными данными которой являются объемы производимых и реализуемых продуктов.
В рассматриваемой модели предлагается отказаться от допущения независимости инвестиционных проектов друг от друга. Это означает, что их денежные потоки уже нельзя принимать как заранее заданные, и они должны определяться как результаты процесса принятия решения. Такое предположение обосновано, когда речь идет о многопродуктовых и/или многоступенчатых процессах производства и при этом нельзя допускать независимость инвестиционных проектов. В этом случае необходимо рассматривать денежные потоки как результат одновременного планирования производственной программы определения программы и программы инвестиций. При значительных объемах производства в рамках формировании инвестиционной программы существенную роль начинают играть нелинейные зависимости. Указанная проблема особенно актуальна при рассмотрении задач стратегического планирования.
Вместе с тем в литературе при решении проблемы одновременного инвестиционного и производственного планирования рассматривается исключительно задача линейного программирования, при этом отмечается, что при значительных увеличениях объемов производства (так называемый «большой» проект) существенную роль начинают играть нелинейные зависимости. В таких условиях представляет определенный научный интерес нелинейная постановка задачи оптимизации, которая позволяет оценивать так называемые «большие проекты».
Между тем стратегическое планирование предполагает и оптимизацию операционной деятельности (которая в нашей модели включает и «основное производство», и участие в реальных инвестиционных и инновационных проектах).
Важная особенность этой деятельности состоит в следующем. От одного варианта финансовой деятельности к другому можно переходить непрерывно, изменяя соответствующие переменные модели. При этом допустимые наборы этих переменных образуют выпуклое множество, а целевая функция оказывается выпуклой функцией этих переменных. С операционной деятельностью положение иное. Здесь также есть управляющие параметры, которые можно изменять «практически» непрерывно (объемы производства продукции, размеры производственных запасов и др.). Однако при этом денежные поступления и расходы могут меняться нелинейно. Так, затраты промышленного предприятия меняются нелинейно при изменении его мощности или удельных весов отдельных видов продукции в общем объеме производства, затраты на железнодорожные перевозки меняются нелинейно при изменении грузопотока по соответствующей линии и т.д.
В этих условиях задача оптимизации операционной деятельности может ставиться следующим образом. Предположим, что фирма может изменять свою операционную деятельность, непрерывно изменяя некоторые управляющие параметры (например, объемы производства отдельных видов продукции или сроки начала отдельных мероприятий), образующие вектор u = (u1, u2, ...). Тогда на каждом шаге t чистый операционный доход Ft и рыночная стоимость основных средств Gt становятся некоторыми функциями от u, которые мы будем считать достаточно «гладкими». После этого из той же модели можно найти оптимальное управление u.
Легко проверить, что теперь в двойственной модели добавятся новые ограничения на каждый управляющий параметр [2]:
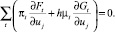
Смысл их предельно прост. Рассмотрим малый проект, состоящий в увеличении параметра πj на малую единицу. Результатом такого проекта будет прирост чистых операционных доходов и рыночной стоимости основных средств соответственно на ∂Ft/∂uj и ∂Gt/∂uj. Если вектор u выбран оптимально, то такой проект не изменит значения критерия (точнее – изменит его на малую величину второго порядка). Это значит, что DEI (приведенный эквивалентный доход) такого проекта, рассчитанный по методике [2], равен 0, что и выражается приведенными выше равенствами.
Рассмотрим интересный частный случай данной задачи. Фирма намечает на шаге 0 изменить свою производственную мощность. Поэтому имеется единственный управляющий параметр u – мощность, которая может меняться непрерывно. Предполагается, что оптимальная мощность положительна, причем при оптимальной политике фирма не упирается в ограничения по объему кредитования (т.е. все qt = 0), а ставка дисконта на всех шагах одна и та же, так что πt – 1/π1 = 1 + Е. Тогда условие, приведенное выше, принимает вид
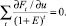
Величины ∂Ft/∂u – приросты чистых денежных притоков фирмы от изменения оптимальной мощности на малую единицу – здесь естественно трактовать как чистые денежные притоки «приростного» проекта малого изменения мощности. Тогда приведенное равенство означает, что ставка дисконта здесь совпадает с ВНД указанного «приростного» проекта и, стало быть, определяется не только доходностями вложений в финансовые активы (ФА), но и доходностью вложений в «собственное производство». Решение при этом оказывается таким, как если бы к числу ФА был добавлен «проект» наращивания мощности на малую единицу (именно потому, что такая единица – малая, этот «проект» правомерно рассматривать как тиражируемый). Другими словами, здесь можно определять ставку дисконта как максимальную доходность альтернативных направлений вложений, включив в число таких направлений «проекты» малого изменения мощности (по сравнению с ее оптимальным, а не существующим уровнем).
Потребность в учете вложений в «собственное производство» интуитивно ощущают и инвесторы, и оценщики, поэтому нередко можно слышать, что при выборе ставки дисконта фирме следует ориентироваться на сложившуюся доходность ее деятельности. Так, в литературе говорится, что при сравнении цен товаров, различающихся сроком службы, за значение ставки дисконта можно принять безрисковую ставку, если покупатель не имеет своего бизнеса, или ставку, равную закладываемой рентабельности собственного бизнеса покупателя или продавца. Между тем теоретически недопустимо приравнивать ставку дисконта к рентабельности собственного бизнеса: сложившаяся (пусть даже стабильная во времени) средняя рентабельность фирмы может существенно отличаться от предельной доходности вложений, однако большие расхождения, скорее всего, встречаются не слишком часто. В то же время даже из указанного неверного положения автор, известный оценщик, делает совершенно справедливый, но идущий вразрез со Стандартами оценки (и потому достаточно смелый) вывод о различиях ставок дисконта у разных участников рынка: следует иметь в виду, что продавец и различные группы покупателей по-разному оценивают для себя ставку дисконтирования: как правило, для большинства покупателей ставка дисконтирования ниже, чем для продавца (поскольку они либо не имеют собственного бизнеса, либо, если имеют, его рентабельность может уступать рентабельности торгового объекта).
Разберемся теперь в следующей интересной проблеме. Предположим, что фирма как-то выбрала ставку дисконта и оценивает методом NPV целесообразность приобретения нового станка. Если NPV (или DEI) проекта такой покупки окажется отрицательным, ситуация ясна: покупка нецелесообразна. Случай NPV = 0, очевидно, маловероятен. Но как поступить, если окажется, что NPV > 0? Казалось бы, ответ очевиден и здесь: станок надо купить. Однако такой ответ формально неверен! Дело в том, что проект покупки станка тиражируем, и каждый дополнительно купленный станок должен улучшить финансовое состояние фирмы. Поэтому представляется, что фирма должна купить как можно больше таких станков. Но ведь это, очевидно, противоречит здравому смыслу! В чем же дело? Оказывается, дело в существенном отличии станков от ФТ: проекты их покупки не являются тиражируемыми, ибо объем покупок влияет на денежные потоки предприятия нелинейно. Допустим, что фирма начала покупать станки по одному. Ее технико-экономические показатели при этом начнут меняться, но их зависимость от количества используемых станков будет нелинейной: чем больше станков купит фирма, тем больше изменений ей придется внести в организацию и технологию производства, в деятельность основных и вспомогательных подразделений, в систему сбыта и рекламы и т.п. Наконец, наступит такой момент, когда покупка следующего станка окажется уже неэффективной. Условно можно сказать, что «доходность» покупки последнего станка при этом сравнялась со ставкой дисконта. Отсюда, кстати, можно сделать и обратный вывод: если рациональная политика фирмы предусматривает покупку станка, то ставка дисконта должна превышать «доходность» этой покупки. И наоборот, если рациональная политика фирмы не предусматривает покупки станка, то ставка дисконта должна быть меньше «доходности» этой покупки. Эти соображения могут оказаться полезными для практических оценок ставки дисконта для конкретных фирм.
Полезно иметь в виду, что приведенные равенства выражают только необходимые, но не достаточные условия оптимальности. Дело в том, что нелинейность функций Ft(u) и Gt(u) часто бывает «плохой». Оптимизационная задача при этом оказывается «невыпуклой» и в ней возникают многочисленные локальные оптимумы, часто довольно далекие от глобального.
В то же время воздействия на операционную деятельность фирмы могут быть и дискретными, а фирма должна выбрать лучший из нескольких возможных вариантов управления (например, вид используемого сырья или его поставщика, тип приобретаемого оборудования или транспортных средств). Говоря об использовании критерия NPV для оценки стоимости проекта, необходимо отметить, что такая оценка должна производиться при наиболее эффективном использовании оцениваемого имущества. Но это как раз и означает, что есть несколько различных способов использования имущества, из которых оценщик должен выбрать наилучший, наиболее приемлемый для фирмы-покупателя. В этом случае мы также имеем дело с задачей дискретной оптимизации операционной деятельности.
Существенно, что во всех задачах такого рода уже нельзя непрерывно переходить от одного варианта управления к другому. В подобных ситуациях «операционная» политика фирмы определяется не только «непрерывно меняющимся» векторным параметром u, но и векторным параметром е, принимающим конечное число значений е1, е2, ... Каждому k – y из этих значений отвечают, вообще говоря, свои функции Fkt(u) и Gkt(u), и соответственно – свое оптимальное управление u и свое значение критерия оптимальности [2]. Поэтому здесь ничего не остается, как рассмотреть каждый допустимый вектор ек в отдельности, решить адекватную оптимизационную задачу, найти соответствующее значение целевой функции и выбрать то k, где это значение будет наибольшим. В общем случае предложить что-то более простое затруднительно, хотя в конкретных задачах, учитывающих специфику дискретно меняющихся параметров, наверняка найдутся более эффективные алгоритмы. Для нас же важно другое: разным ек отвечают, вообще говоря, разные оценки pit и qt, а следовательно, и разные αt и yt. Поэтому, если даже мы знаем ставки дисконта и оценки прав заимствования, относящиеся к некоторому допустимому вектору е1, их нельзя использовать, чтобы оценить эффективность выбора другого допустимого вектора е2 (особенно, если переход от е1 к е2 связан с кардинальными изменениями в функционировании фирмы). Другими словами, если имеется несколько кардинально различающихся вариантов развития фирмы (а именно такие варианты чаще всего рассматривают при стратегическом планировании), для выбора лучшего из них нельзя использовать локальный критерий оптимальности (ни NPV, ни какие-либо его модификации). Необходимо использовать нелинейную модель.
Нелинейная модель
Переменные модели
ct – свободные денежные средства (в кассе) в момент времени t;
mjkt – число продуктов типа k, которые в момент времени t производятся на оборудовании типа j;
xjt – число инвестиционных объектов типа j, которые приобретаются в момент времени t.
Константы
Ajt – платеж за приобретение одного комплекта оборудования типа j в момент времени t;
Bj – начальная мощность всех видов оборудования типа j;
Ct – избыток или недостаток финансовых средств инвестора в момент времени t;
Djk – среднее время производства продукта k на оборудовании типа j;
Ft – относительная величина дохода инвестора в момент времени t (элемент вектора структуры дохода);
Hkt – максимальный объем сбыта продукта типа k в момент времени t;
Ljt – выручка от ликвидации одного комплекта оборудования типа j, которую получает инвестор в момент времени T, если он продает это оборудование в момент времени t;
Mt – базовый платеж в момент времени t;
Pkt – чистая цена продажи продукта типа k, который продается в момент времени t;
Vjk – средние переменные производственные издержки продукта типа k, который производится на оборудовании типа j;
Y – уровень дохода инвестора;
Zj – мощность одного оборудования типа j в один период.
Индексы
j – индекс типа оборудования (j = 1, …, J);
k – индекс продуктов (k = 1, …, K);
t – временной индекс (t = 1, …, T).
Формулировка модели
Целевая функция. В задаче предполагается максимизировать собственный капитал к концу рассматриваемого процесса и одновременно осуществить фиксированный, заранее заданный доход от производственной деятельности предприятия.
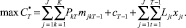 (1)
(1)
Ограничения. При максимизации представленной целевой функции необходимо принять во внимание следующие три вида дополнительных ограничений, отражающих условия ликвидности, производства и сбыта.
Условия ликвидности. Условия является ликвидными, если поступления ни в какой из моментов времени планового периода не меньше выплат. Поэтому из полного финансового плана для момента времени t = 0:
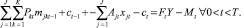 (2)
(2)
При этом CT символизирует неизвестную перед началом решения проблемы (максимизируемую) стоимость собственного капитала. Если перенести константы в правую часть и, кроме того, потребовать, чтобы остаточное имущество не могло стать меньше 0, то тогда формулировка условия ликвидности будет выглядеть следующим образом:
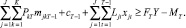 (3)
(3)
Условия производства. Условия производства являются ядром каждой модели одновременного инвестиционного и производственного планирования. Ни в какой из моментов времени планового периода нельзя произвести больше продуктов, чем это позволяют мощности, которыми располагает предприятие в это время. В данной работе, в отличие от предпосылок общепринятой (классической) модели производственного планирования [1 c. 196], мощность оборудования не является неизменной: ее можно увеличить с помощью инвестиций. Важно подчеркнуть, что связь между увеличением мощности и выпуском продукции носит нелинейный характер. Имеющиеся в распоряжении в момент времени t при 0 < t < T мощности оборудования типа j определяют следующее ограничение:
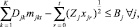 t < T (4)
t < T (4)
Эти ограничения необходимо учитывать для всех типов оборудования и для всех моментов времени планового периода.
Условия сбыта. В соответствии с допущениями модели длительность производства продуктов в точности равна одному периоду. Продукты не складируются, и существуют верхние границы сбыта. Поэтому необходимо соблюдать дополнительные ограничения:
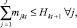 t < T. (5)
t < T. (5)
Этих дополнительных условий необходимо придерживаться для всех видов продуктов и для всех моментов времени планового периода.
Условия целочисленности. Так как невозможно приобрести части оборудования, мы также должны требовать, чтобы имело место следующее:
xjt целое число ∀j, t < T. (6)
В ходе исследования рассматривался числовой пример, который иллюстрирует построение модели и делает более понятной работу ее компонентов.
Для решения поставленной задачи была построена базовая таблица в Excel. Она содержит 21 переменную, 1 целевую функцию и 16 дополнительных ограничений.
В результате решения задачи с помощью алгоритмов Excel (процедура «Поиск решения»), были получены значения, которые существенно отличаются от линейного варианта.
Выводы
В представленной модели использовалась нелинейная зависимость между инвестициями на приобретение дополнительного оборудования (мощностью) и объемом выпускаемой продукции. Решение показало существенное отличие от линейного варианта, т.е. традиционного метода. Это принципиальная вещь, которая позволяет по-новому взглянуть на существующую проблему:
1) во-первых, представленная модель по сравнению с линейным вариантом дает более точную оценку исследуемых проектов модернизации;
2) во-вторых, нелинейная модель позволяет поставить и решить задачу оптимизации для отдельного (индивидуального) проекта автономно, локально, рассматривая его как так называемый «большой проект», который не может быть исследован стандартными методами с использованием NPV.



