Электронные устройства на вакуумных лампах широко применяются в ряде отраслей техники. В частности, до сих пор разрабатываются и производятся ламповые гитарные усилители. В области звуковой аппаратуры полупроводниковая аналоговая техника до сих пор не смогла полностью вытеснить ламповую, поскольку характер нелинейного искажения сигнала на транзисторах и лампах отличается в силу различия физических принципов работы этих приборов [5]. Цифровая эмуляция ламповых устройств также далека от высокой степени реалистичности, поскольку, с одной стороны, до сих пор не решена задача точной идентификации вакуумных приборов, с другой, уравнения высокого порядка, описывающие ламповый усилитель, являются нелинейными и жесткими, что затрудняет их численное решение в реальном масштабе времени [5].
Для эффективного решения дифференциальных уравнений на всех классах вычислителей, в том числе в реальном времени, в современной вычислительной математике используются аппаратно-ориентированные методы численного интегрирования [1]. В данной статье рассматривается моделирование триодного усилительного каскада с помощью аппаратно-ориентированных методов интегрирования. Изучены вопросы математического описания нелинейных электрических цепей с вакуумными приборами, предложена улучшенная модель триода и ее численные параметры для триода 12AX7. Рассматриваются экстраполяционные методы численного решения дифференциально-алгебраических уравнений на основе неявного метода Эйлера и новое семейство вещественно-неявных методов Рунге ? Кутты, эффективно реализуемых на вычислителях с параллельной архитектурой. Проводится экспериментальное сравнение двух аппаратно-ориентированных методов между собой и с другими известными численными методами.
Математическая модель триодного усилительного каскада
На рис. 1, а представлен фрагмент цепи гитарного предусилителя – триодный усилительный каскад [3].
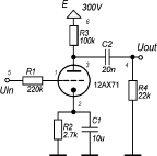
а б
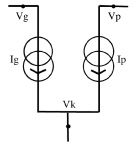
Рис. 1. Типовая схема включения триода и схема его замещения. Цифрами обозначены номера узлов при составлении уравнения
Традиционным средством расчета цепей в средах автоматизированного проектирования выступает модифицированный метод узловых напряжений (МУН). Его можно рассматривать как метод формализации записи уравнений цепи с использованием законов Кирхгофа. Если цепь не содержит индуктивностей, то она может быть описана матричным уравнением вида
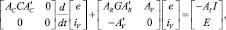(1)
где e – напряжения в узлах; iV – токи, протекающие через источники напряжения; AC, AR, AV, AI – матрицы инцидентности конденсаторов, резисторов, источников напряжений и токов соответственно; C = diag{C1, C2, ...} – диагональная матрица номиналов конденсаторов;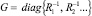 
– диагональная матрица номиналов проводимостей; I, E – векторы значений токов и напряжений соответствующих источников.
Для цепи, показанной на рис. 1, а, матрицы инцидентности будут иметь следующий вид:
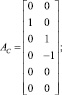
откуда следует общий вид матричного уравнения цепи:
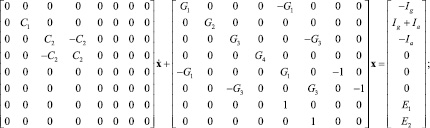
Поскольку триод замещается схемой из двух управляемых источников тока (рис. 1, б) и при этом в ламповых схемах отсутствуют независимые источники тока, уравнение (1) можно записать в компактном виде
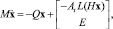(2)
где At – матрица инцидентности источников тока Ig и Ia, которыми замещается триод; L – нелинейная функция токов через триод, а
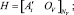
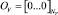(3)
– матрица инцидентности, такая, что Hx = Vt – напряжения между узлами, к которым подключен триод, а NV – число источников напряжения.
Статическая модель триода 12AX7
В литературе рассматриваются несколько различных моделей, описывающих токи, протекающие через триод. Самая простая из данных моделей получила название «закон степени трех вторых», или закон Чайлда – Ленгмюра:
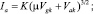
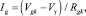(4)
где K, μ, Vr, и Rgk – параметры модели. Хотя формула (4) и основана на интерпретации физических принципов работы электровакуумных приборов, она описывает ток сетки неточно, имея ряд ограничений на входные напряжения и требуя представления в виде кусочной функции с разрывами производной. Более совершенна эвристическая модель триода Нормана – Корена, однако наиболее точной на настоящий момент является модель Демпвольфа – Зольцера [4]:
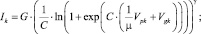
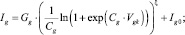(5)
где G и Gg – постоянные пространственного заряда, а степенные показатели γ и ξ и коэффициенты C и Cg являются эвристическими параметрами модели. Анодный ток в модели Демпвольфа – Зольцера рассчитывается как разница токов катода и сетки:
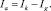
Данный факт одновременно является и одним из недостатков данной модели. Если коэффициенты уравнения сеточного тока требуется подкорректировать для лучшего согласования с данными измерений, то необходимо вместе с ними модифицировать и коэффициенты тока Ik. Это может быть исправлено путем замены числовых коэффициентов, с помощью выражения для Ik рассчитывая Ia:
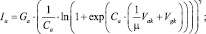
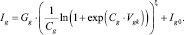(6)
Помимо высокой степени адекватности положительным свойством модели Демпвольфа – Зольцера (5) и ее модифицированной версии (6) является то, что она имеет аналитическую производную без разрывов. Это позволяет сократить время вычислений якобиана и обеспечить лучшую сходимость решения.
Численные параметры для модели (6), полученные на основе уточненных измерений вольт-амперных характеристик триода 12AX7 для тока анода:
Gp = 1,73?10–3; μ = 88,74;
γ = 1,303; Cp = 4,032.
Для тока сетки:
Gg = 8?10–4; ξ = 2,2; Cg = 6; Ig0 = 4,6?10–9.
Численное решение дифференциально-алгебраических уравнений
Рассмотрим решение частного случая дифференциально-алгебраического уравнения – полуявного дифференциального уравнения вида
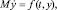(7)
где M – некоторая матрица; t – независимая переменная (время), а f(t, y) – некоторая, в общем случае нелинейная, функция, которую мы будем называть функцией правой части (ФПЧ). Формула для s-стадийного метода Рунге – Кутты решения ДАУ в переменных z [2]:
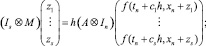
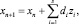(8)
где d = bA–1; Ij – единичная матрица размерности j×j, а ⊗ – умножение Кронекера, а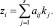 
Решение уравнения (8) осуществляется с помощью итераций Ньютона. Перенеся все члены в правую часть уравнения (8), введем функцию
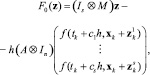. (9)
Для нее необходимо найти корень z*. Тогда метод Ньютона может быть записан следующим образом:
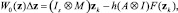(10)
где W0 – якобиан функции F0. Затем определяется новое значение вектора переменных
zk + 1 = zk + Δz.
Уравнение нелинейной цепи с триодами может быть решено методами Рунге – Кутты путем выделения правой части уравнения (2)
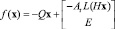(11)
и нахождения ее якобиана:
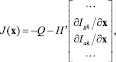(12)
где
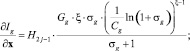
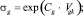
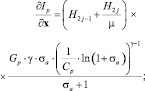
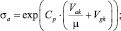
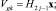
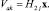
Вещественно-неявные методы Рунге – Кутты
Идея распараллеливания неявных методов Рунге – Кутты состоит в том, чтобы вычислять s независимых компонент вектора Δzk в параллельных потоках. Действительно, если матрица метода может быть представлена в виде
то после замены переменных
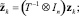
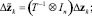
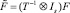
итерационная схема (9) преобразуется к виду
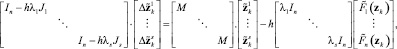
где Ji = ∂f ? ∂y(t0 + cih, y0 + zi) – якобиан функции правой части в точке (t0 + cih, y0 + zi). Такие методы будем называть вещественно-неявными методами Рунге – Кутты или ВНРК (англ. Really Implicit Runge-Kutta, RIRK). Заметим, что λi – неравные вещественные числа, и λi ≠ λj, i ≠ j, в противном случае матрица T сингулярная и T–1 не существует. С помощью подходов многокритериальной оптимизации был синтезирован 3-стадийный L-устойчивый метод 3-го порядка, который в дальнейшем использовался для численного решения уравнения цепи:
Численное моделирование цепи с вакуумным триодом
Рассмотрим моделирование триода (2) с использованием различных численных методов. Предполагается, что все составляющие входного сигнала частотой выше 20 кГц подавляются входным фильтром. При базовой частоте дискретизации 44 кГц были рассмотрены следующие варианты передискретизации L: величина передискретизации в 4 раза (частота обработки данных 176 кГц), в 8 раз (352 кГц) и в 16 раз (704 кГц). В качестве входного сигнала был выбран синусоидальный сигнал амплитудой 10 В с частотой, изменяющейся во времени по логарифмическому закону.
Было обнаружено, что задача моделирования триодного каскада является жесткой, и для всех рассмотренных численных методов происходит потеря порядка алгебраической точности.
Эксперименты показывают, что коэффициент передискретизации оказывает существенное влияние на необходимое количество итераций Ньютона для достижения требуемой точности. Однако в этом случае повышается и число обращений к функции правой части, что влечет за собой увеличение числа выполняемых алгебраических операций.
Как видно из графика на рис. 3, наилучшую вычислительную эффективность обеспечивает метод ВНРК33, обладая точностью порядка 1 и 0,1 % при частотах дискретизации 352 и 704 кГц соответственно. Если допустимы искажения сигнала в пределах 5 %, то наименьших затрат вычислительных ресурсов требует экстраполяционный решатель второго порядка точности на основе неявного метода Эйлера.
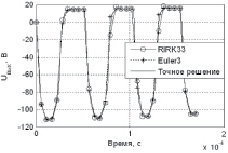
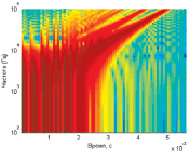
Рис. 2. Сравнение точного отклика модели при частоте входного сигнала 20 кГц с откликом модели с L = 4, а также спектрограмма выходного сигнала триодного каскада
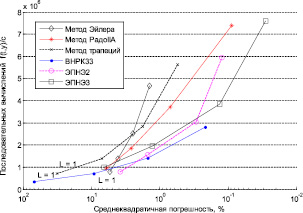
Рис. 3. Погрешность моделирования при различных коэффициентах передискретизации: L = [1; 2; 4; 8]
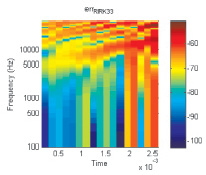
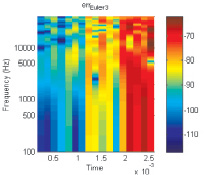
Рис. 4. Сравнение спектра погрешностей метода RIRK33 и ЭПНЭ3 при восьмикратной передискретизации
Традиционно применяемые в форме дискретных подстановок методы аппаратного моделирования – неявный метод Эйлера и метод трапеции – показывают наихудшие результаты по вычислительной эффективности при моделировании нелинейной цепи.
Сравнение результатов (рис. 4) показывает, что основная погрешность решения неявным экстраполяционным методом Эйлера третьего порядка сосредоточена в верхней части спектра, в то время как для метода ВНРК33 характерно более равномерное распределение погрешности по частоте с присутствием высших гармоник на всех частотах входного сигнала. Из всего вышесказанного можно сделать вывод, что предлагаемый вещественно-неявный трехстадийный метод Рунге – Кутты является оптимальным при решении задачи программно-аппаратного моделирования цепи с вакуумным триодом.
Заключение
В статье рассмотрено моделирование триодного усилительного каскада с применением аппаратно-ориентированных методов численного интегрирования. Установлено, что при решении жестких нелинейных задач наиболее целесообразно применение метода ВНРК третьего порядка с ограниченным числом итераций Ньютона, или же экстраполяционного неявного метода Эйлера второго порядка. При этом выбор метода для конкретного приложения можно производить, исходя из анализа спектра погрешности получаемого решения.
Дальнейшим направлением исследований является моделирование цепей с большим количеством вакуумных приборов, описываемых дифференциально-алгебраическими уравнениями высокого порядка, а также апробация предложенных аппаратно-ориентированных методов при аппаратной реализации эмуляторов гитарных ламповых усилителей.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований в рамках договора № НК 14-01-31277\14 от 06.02.2014 г.