Манипуляторы параллельной структуры находят все большее применения в отраслях промышленности в таких странах, как Япония, США, Китай, при выполнении различных работ. Это связано с их положительными свойствами: маштабируемостью, хорошим соотношением полезной нагрузки к массе гибких связей манипулятора [1, 4].
Требуется определить параметры движения нагруженного схвата параллельного манипулятора с гибкими звеньями, вызванного действием внешней возмущающей силы, обозначенной как Fвн на рис. 1.
Известно, что действие веса груза mg создает в звеньях параллельного манипулятора усилия, обозначенные через T1, T2, T3, T4 на рис. 1.
В работе [2, 3] получены уравнения, позволяющие рассчитать значение усилий в звеньях манипулятора в зависимости от положения нагруженного. Добавив к данным уравнениям вектор внешней возмущающей силы Fвн, получим
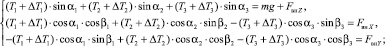(1)
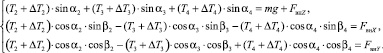(2)
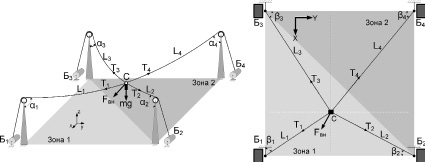
а б
Рис. 1. Геометрическая интерпретация процесса распределения усилий в звеньях параллельного манипулятора: а – общий вид; б – в плоскости XOY; где Б1, Б2, Б3, Б4 – барабаны, осуществляющие изменение длины звеньев манипулятора; P1, P2, P3, P4 – ролики; C – схват с грузом; mg – вектор силы тяжести
В уравнениях (1) и (2) T1, T2, T3, T4 – измеренные значения усилий в соответствующих звеньях манипулятора при отсутствии внешней возмущающей силы Fвн, которая представлена в виде проекций на оси декартовой системы координат FвнX, FвнY, FвнZ; ΔT1, ΔT2, ΔT3, ΔT4 – приращения усилий в звеньях манипулятора, вызванные действием внешней возмущающей силы Fвн. Коэффициенты sinα1, sinα2, sinα3, sinα4, cosα1, cosα2, cosα3, cosα4, sinβ1, sinβ2, sinβ3, sinβ4, cosβ1, cosβ2, cosβ3, cosβ4 получены с использованием методом элементарной геометрии [5].
Выразив искомые компоненты вектора внешней возмущающей силы Fвн (FвнX, FвнY, FвнZ) из уравнений (1), (2), получим следующие аналитические формулы:
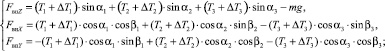(3)
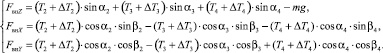(4)
Таким образом, по измеренным значениям полных усилий в звеньях параллельного манипулятора и использованию полученных аналитических выражений (3) и (4) возможно определить направление и величину вектора внешней возмущающей силы, прикладываемой к точке крепления нагруженного схвата.
При решении данной задачи примем допущение о том, что приложенное к точке крепления схвата с грузом внешнее возмущающее воздействие в виде силы Fвн не изменяет своей величины, а также направления действия. В этом случае нагруженный схват манипулятора будет перемещаться по линейной траектории из точки Мнач(xнач, yнач, zнач) в точку Мкон(xкон, yкон, zкон) с постоянной линейной скоростью, определяемой величиной внешней возмущающей силы Fвн. Так как координаты (xнач, yнач, zнач) точки Mнач, определяющей начало отрезка линейной траектории движения нагруженного схвата известны, то координаты (xкон, yкон, zкон) точки Mкон можно вычислить следующим образом:
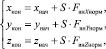(5)
где – величина пути, пройденного схватом с грузом, на протяжении которого действовала внешняя возмущающая сила Fвн, FвнXнорм, FвнYнорм, FвнZнорм – нормированные компоненты вектора Fвн, определяемые как
(6)
Когда ведущей координатой является координата x, ведомые координаты y и z могут быть вычислены по следующим уравнениям:
(7)
где xнач ≤ x ≤ xкон. Если ведущей является координата y, то ведомые координаты x и z могут быть вычислены следующим образом:
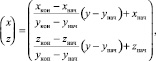(8)
где yнач ≤ y ≤ yкон. По аналогии с (7) и (8), если ведущей является координата z, то ведомые координаты x и y можно найти из уравнений
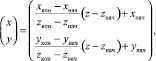(9)
где zнач ≤ z ≤ zкон. Подставив (8) в (3), получим закон изменения обобщенных координат L1, L2, L3 и L4 вдоль линейной траектории, заданной двумя точками Mнач и Mкон в пространстве:
(10)
Для определения скорости изменения обобщенных координат v1, v2, v3 и v4 при движении нагруженного схвата манипулятора вдоль отрезка прямой с постоянной линейной скоростью v используем векторный метод, сущность которого поясняет рис. 2.
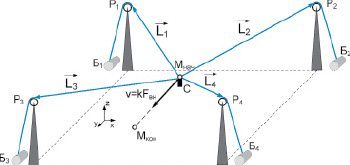
Рис. 2. Схема к задаче о нахождении обобщенных скоростей
При использовании векторного подхода звенья манипулятора представим в виде векторов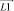 
, 
, 
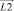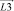и 
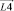, величина которых является нормированной относительно длин звеньев. Тогда координаты данных векторов можно определить по формулам
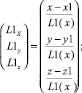
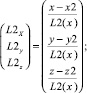
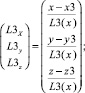
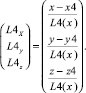
Используя известные методы аналитической геометрии, величины обобщенных скоростей v1, v2, v3 и v4 определим как проекции вектора линейной скорости v на вектора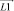 
, 
, 
, 
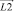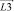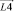, то есть
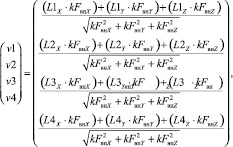(11)
где k – некоторый постоянный коэффициент передачи, связывающий величину внешней возмущающей силы Fвн и линейной скорости движения нагруженного схвата манипулятора v.
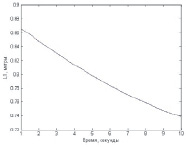
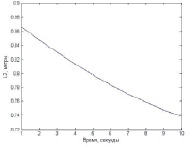
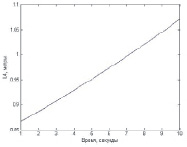
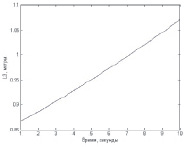
Рис. 3. Изменение длин тросов для перемещения нагруженного схвата согласно заданному вектору внешней силы
Для проверки адекватности полученной математической модели с использованием среды Matlab 7.11.0 (R2010b) была разработана компьютерная модель, позволяющая для заданной конфигурации параллельного манипулятора (координатам установки вертикальных колонн (x1, y1, z1), (x2, y2, z2), (x3, y3, z3), (x4, y4, z4)), веса груза mg, его начальным координатам (xнач, yнач, zнач), а также величинам приращения усилий в его звеньях ΔT1, ΔT2, ΔT3, ΔT4, вызванным воздействием внешней возмущающей силы Fвн, рассчитать координаты вектора Fвн, а также изменение длин и скоростей обобщенных координат при движении нагруженного схвата вдоль линейной траектории, определяемой величиной и направлением силы Fвн.
Результаты компьютерного моделирования для случая, когда вертикальные колонны установлены в точках P1(1; 0; 1), P2(1; 1; 1), P3(0; 0; 1), P4(0; 1; 1), вес груза mg = 1, координаты точки, определяющей его начальное положение в пространстве Mнач (0,5;0,5;0,5), вектор внешней возмущающей силы направлен параллельно плоскости XOY и величины приращений ΔT1 = 0,87, ΔT2 = 0,015, ΔT3 = –0,85, ΔT4 = 0, представлены на рисунках.
В настоящей статье приведена математическая модель, позволяющая определить вектор внешней возмущающей силы по величине усилий в звеньях параллельного манипулятора. В результате полученных систем нелинейных уравнений математическая модель позволяет отслеживать усилие не только в горизонтальной плоскости, но также в любом 3D направлении. Также данная система позволит в режиме реального времени отслеживать текущее внешнее усилие и регулировать скорость перемещения груза. В среде Matlab была разработана компьютерная модель. В результате моделирования получены результаты, которые свидетельствуют об адекватной полученной математической модели.
Данные исследования могут быть использованы при проектировании САУ данного манипулятора с целью транспортировки груза за счет прямого влияния на процесс перемещения. влияния на процесс перемещения.
Работа выполнена в рамках гранта (проекта) РФФИ 14-08-31484.