В современной вычислительной математике выделяется направление так называемых аппаратно-ориентированных численных методов интегрирования – алгоритмов численного решения обыкновенных дифференциальных уравнений, пригодных для использования как на компьютерах общего назначения, так и во встраиваемых системах. Сформулируем некоторые из требований к таким методам [1]:
1. Метод должен быть самостартующим.
2. Метод должен обладать устойчивостью, достаточной для реализации поставленной задачи на всей совокупности аппаратных средств при заданных параметрах дискретизации.
3. Метод должен работать с равномерной выборкой точек входного сигнала.
4. Алгоритм метода должен предусматривать возможность распараллеливания решения на вычислителе с соответствующей архитектурой.
5. При реализации на персональном компьютере метод должен показывать вычислительную эффективность, сопоставимую с таковой для известных методов.
6. Алгоритм метода должен быть мало подвержен влиянию ошибок округления и вычислительной погрешности.
Первое требование исключает многошаговые методы, широко применяемые в настоящее время в САПР радиоэлектронных устройств. Второму требованию не соответствуют любые полностью явные численные методы. Третье и пятое требования исключают применение большинства неявных методов Рунге – Кутты. С учетом четвертого требования на роль аппаратно-ориентированных методов претендуют:
1) неявные методы семейства Рунге – Кутты особого вида;
2) экстраполяционные методы с неявными опорными методами;
3) экстраполяционные методы с полунеявными опорными методами.
В настоящей статье рассматриваются представители первых двух классов алгоритмов: экстраполяционный метод на основе неявного метода Эйлера и трехстадийный вещественно-неявный метод Рунге – Кутты третьего порядка. Проводится практическое сравнение данных аппаратно-ориентированных методов между собой и с другими численными методами на ряде тестовых задач при последовательной и параллельной реализации.
Постановка задачи. Общий вид неявных методов Рунге – Кутты
Рассмотрим решение обыкновенного дифференциального уравнения
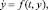 (1)
(1)
где t – независимая переменная (время), а f(t, y) – некоторая, в общем случае нелинейная, функция, которую мы будем называть функцией правой части (ФПЧ). Переформулируем стандартную запись методов Рунге ? Кутты, введя обозначение
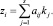
Здесь zi = ki – y0. Тогда, учитывая, что 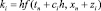 [4]:
[4]:
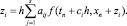 (2)
(2)
Из (2) следует общая форма записи для s-стадийного метода Рунге ? Кутты в новых переменных z:
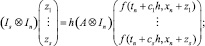
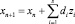 , (3)
, (3)
где d = bA–1, Ij – единичная матрица размерности j×j, а ⊗ – умножение Кронекера. Решение уравнения (2) осуществляется с помощью итераций Ньютона, общий вид которых
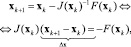
при этом отыскивается такое значение x*, при котором F(x*) = 0.
Для схемы (3) метод Ньютона может быть записан следующим образом:
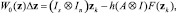 (4)
(4)
где W0 – якобиан функции F0. Затем определяется новое значение вектора переменных:
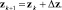
Вещественно-неявные методы Рунге – Кутты
Идея распараллеливания методов Рунге – Кутты состоит в том, чтобы вычислять s независимых компонент вектора Δzk в параллельных потоках. Действительно, если матрица метода может быть представлена в виде

то после замены переменных
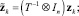
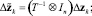
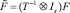
итерационная схема (3) преобразуется к виду
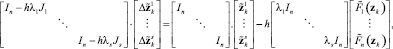
где Ji = ∂f ? ∂y(t0 + cih, y0 + zi) – якобиан функции правой части в точке(t0 + cih, y0 + zi). В конце каждой итерации потоки собираются, преобразуются в старую систему координат. Такие методы будем называть вещественно-неявными методами Рунге ? Кутты, ВНРК (англ. Really Implicit Runge-Kutta, RIRK). Заметим, что λi ≠ λj, i ≠ j, в противном случае матрица T сингулярная и T–1 не существует. С помощью подходов многокритериальной оптимизации авторами был синтезирован L-устойчивый метод 3-го порядка, имеющий таблицу Бутчера
 (5)
(5)
собственные векторы матрицы A которого порождают матрицу
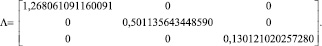
Область устойчивости метода (5) приведена на рис. 1.
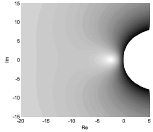
Рис. 1. Область устойчивости вещественно-неявного метода (5)
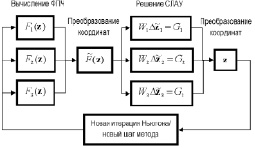
Рис. 2. Схема параллельного решателя на основе трехстадийного метода ВНРК
На рис. 2 представлена архитектура параллельного решателя ОДУ на основе ВНРК. В случае если применяемый вычислитель поддерживает работу с комплексными числами, подобная организация вычислений теоретически возможна и для методов с комплексными элементами матрицы Λ. Однако на практике оказывается, что точность решения такими методами существенно ниже по сравнению с использованием непреобразованной матрицы A.
Экстраполяционные методы
Идея экстраполировать решения, взятые с разным шагом интегрирования, для повышения порядка точности метода лишь немного моложе классических разностных схем Рунге – Кутты. Предложенный Ричардсоном [5] способ экстраполяции получил свое развитие в работах Грэгга, Булирша, Штёра [3], а также многих других авторов. По сравнению с методами Рунге – Кутты, экстраполяционные методы, с одной стороны, требуют большего числа вычислений функции правой части на шаге. С другой стороны, такие методы обладают способностью организации вычислительных потоков с единственным обменом данных на шаге, а не с двумя, как в случае ВНРК, что сокращает накладные расходы.
Суть экстраполяционных методов заключается в следующем. Выберем ряд натуральных чисел
n1 < n2 < n3... (6)
и определим соответствующие длины шагов, относящиеся к исходному шагу H как
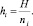
После этого c помощью так называемого опорного метода вычислим значения функции y в точке t0 + H, используя различные длины шагов:
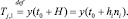 (7)
(7)
Затем применим алгоритм рациональной интерполяции Эйткена – Невилла, результатом которого является так называемая экстраполяционная таблица:
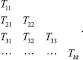
Первый столбец таблицы формируется по формуле (7). Последующие колонки заполняются с помощью рекурсивной формулы [4]:
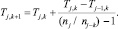
В качестве опорного метода выберем неявный метод Эйлера первого порядка, исходя из выдвинутых требований к устойчивости разностной схемы, а в качестве экстраполяционной последовательности – ряд натуральных чисел. На рис. 3 показана архитектура параллельного решателя на основе экстраполяционного метода третьего порядка. Если максимальное число итераций Ньютона в блоках пропорционально шагу, метод может быть эффективно разделен на три вычислительных потока. Максимальное число итераций Ньютона может быть выбрано как
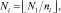
где N1 – число итераций Ньютона на 1-й стадии экстраполятора.
Экспериментальная оценка свойств численных методов
Оценим свойства предложенных аппаратно-ориентированных методов, рассмотрев решение популярных тестовых задач.
Задача VDPL – уравнение осциллятора Ван дер Поля
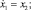
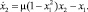
При моделировании используется значение μ = 4.
BRUS – модель циклической химической реакции, предложенная Лефевером и Николисом в 1971 г. и известная в литературе [4] как «брюсселятор»:
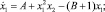
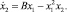 (8)
(8)
Параметры системы (8) выбраны следующим образом: A = 2, B = 8,553.
SPRG – система уравнений Case G, предложенная Спроттом в 1994 г. и описывающая хаотическую нелинейную динамическую систему:
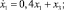
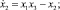
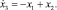
ROBER – разноскоростная система уравнений, описывающая автокаталитическую реакцию Робертсона:
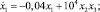
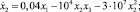
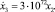
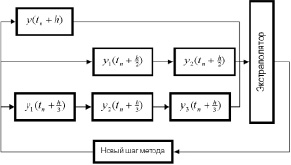
Рис. 3. Организация параллельных вычислений экстраполяционным методом третьего порядка в двух или трех потоках
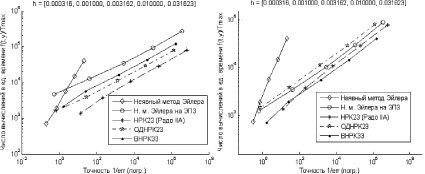
а б
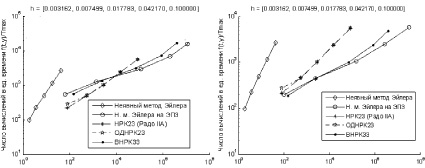
в г
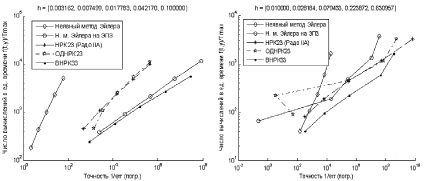
д е
Рис. 4. Сравнение эффективности численных методов интегрирования на задачах: BRUS при последовательной (а) и параллельной (б) реализациях, VDPL при последовательной (в) и параллельной (г) реализациях, SPRG (д) и ROBER (е) при параллельной реализации
Результаты решения тестовых задач аппаратно-ориентированными методами сравним с решениями, полученными неявным методом Эйлера, двухстадийным методом Радо IIA 3-го порядка и двухстадийным методом ОДНРК 3-го порядка, описанным Р. Александером [2]
Оба исследуемых аппаратно-ориентированных алгоритма разделены на три вычислительных потока. Метод ВНРК исследовался при 10 итерациях Ньютона, а ЭПНЭ3 – на последовательности итераций [10, 5, 3] для различных значений шага. Для оценки погрешности использовалось эталонное решение, рассчитанное методом высокого порядка с шагом в 100 раз меньшим, чем шаг тестируемых методов. Представлены графики отношения числа вычислений в единицу времени к достигаемой точности решения.
Заключение
В статье рассмотрено решение ряда нелинейных дифференциальных уравнений с применением аппаратно-ориентированных методов численного интегрирования. Показано, что оба рассмотренных класса методов – экстраполяционные на основе неявного метода Эйлера и вещественно-неявные методы Рунге – Кутты – являются аппаратно-ориентированными с точки зрения критериев 15, приведенных во введении.
Анализ экспериментальных данных показывает, что при параллельной реализации метод ВНРК почти всегда оказывается самым экономичным по числу вычислений функции правой части f(t, y). При этом на задачах Спротта и Робертсона он показывает лучшую точность. Несмотря на то, что неявный экстраполяционный метод Эйлера имеет в большинстве случаев более высокую вычислительную сложность (кроме задачи VDPL), он в то же время наименее подвержен негативному влиянию машинного шума коэффициентов.
Дальнейшим направлением исследований является исследование решения аппаратно-ориентированными методами задач высокого порядка, а также разработка методов ВНРК более высокого порядка точности с аналитической формулировкой коэффициентов.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований в рамках договора № НК 14-01-31277\14 от 06.02.2014 г.



