Рассмотрим задачу Коши для линейного дифференциального уравнения второго порядка
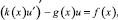0 < x < l; (1)
u(0) = 0;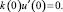 
(2)
Будем предполагать, что коэффициенты и правая часть уравнения (1) удовлетворяют условиям: k(x) ∈ C3[0, l]; g(x), f(x) ∈ C2[0, l]; c2 ≥ k(x) ≥ c1 > 0;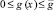 
.
Известно [5], что решение задачи (1)–(2) существует и единственно в классе функций C4[0, l]. Однако это решение, как показано в [2], при больших значениях l может оказаться неустойчивым. Это означает, что сколь угодно малые изменения начальных условий могут вызвать сколь угодно большие изменения решения при больших значениях l. В этом случае сложно получить указанное решение численно, так как ошибки округления и усечения оказывают такое же влияние, как и изменение начальных условий, и приводят к тому, что решение становится неограниченным.
Проинтегрировав уравнение (1) по отрезку [0, l] и воспользовавшись начальным условием (2), приходим к эквивалентной задаче
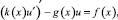x ∈(0, l); (3)
u(0) = 0; (4)
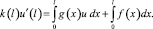(5)
На равномерной сетке
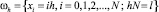
задачу (3)–(5) аппроксимируем конечно-разностной схемой
i = 1, 2, ..., N – 1;
y0 = 0; (6)
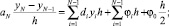
где
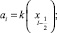di = g(xi); φi = f(xi). (7)
Нетрудно показать, что разностная схема (6) аппроксимирует дифференциальную задачу (3)–(5) с точностью 0(h2). Используя обозначения [3]
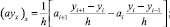
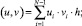
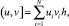
перепишем задачу (6) в форме
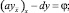(8)
y0 = 0; 
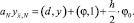(9)
Нетрудно показать единственность решения задачи (8), (9). Действительно, есл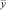и 
и 
– два решения задачи (8), (9), то, очевидно, разность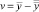 
будет решением задачи
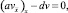i = 1, 2, ..., N – 1, (10)
v0 = 0;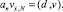 
(11)
Суммируя (10) по i от 1 до N – 1, приходим к равенству
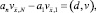
из которого следует, с учетом условия (22), что 
Таким образом, сеточная функция v будет решением конечно-разностной задачи Коши
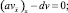v0 = 0; 
из которой следует, что vi = 0, i = 0, 1, ..., N, что означает единственность решения задачи (8), (9).
Будем искать решение задачи (8), (9) в виде
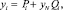i = 0, 1, ..., N, (12)
где Pi и Qi – сеточные функции, определенные на сетке ωh, как решения разностных задач:
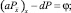P0 = 0; PN = 0; (13)
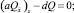Q0 = 0; QN = 1, (14)
где коэффициенты a, d и правая часть φ определены по формулам (7). Как известно [3], задачи (13) и (14) однозначно разрешимы в силу условий на a, d.
Для решения задачи (13) имеет место априорная оценка [4]
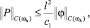(15)
а для решения задачи (14) имеет место равномерная оценка
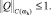(16)
Непосредственной подстановкой можно убедиться, что функция y, определенная по формуле (12), удовлетворяет уравнению (8) и начальному условию y0 = 0. Подставив (12) в нелокальное условие (9), приходим к равенству
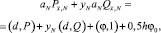
откуда выражаем yN:
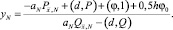(17)
Покажем ограниченность yN. Преобразуем правую часть (17). Суммируя уравнение (13) по i от 1 до N – 1, приходим к равенству
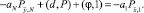(18)
Суммируя уравнение (14) по i от 1 до N – 1, получаем
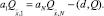(19)
С учетом (18) и (19) выражение (17) для yN принимает вид
(20)
Оценим снизу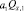 
. Это число не может быть отрицательным, что противоречило бы принципу максимума [3] первой краевой задачи для уравнения (14). Также 
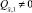, это противоречит условию QN = 1. Следовательно, 
.
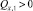Пусть ri – сеточная функция, определенная на ωh, и является решением разностной задачи
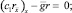r0 = 1; rN = 0. (21)
Умножим уравнение (21) скалярно на Q, а уравнение (14) скалярно на r и вычтем почленно одно из другого. Применяя разностную формулу интегрирования по частям [3] и учитывая краевые условия (14), (21), приходим к равенству
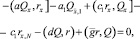
откуда находим
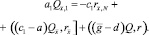(22)
Нетрудно показать, что для всех i = 1, 2, ..., N выполняются неравенства
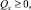
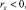Q ≥ 0, r ≥ 0.
С учетом этих оценок из (22) получаем
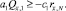(23)
Оценим снизу выражение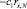 
. Используя точное решение задачи (21), находим, что
,
где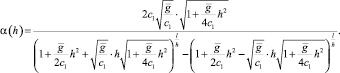 
Положив
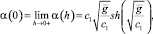
на отрезке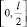 
получим непрерывную, возрастающую по h функцию. Следовательно, для любого 
имеет место неравенство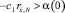 
. Таким образом, 
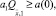откуда следует, что
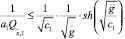(24)
Теперь оценим сверху модуль выражения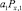 
. Умножая скалярно разностное уравнение (13) на сеточную функцию 
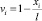, определенную на ωh, получим
(25)
Применяя разностную формулу интегрирования по частям [4] в (25) и учитывая краевые условия (13) и равенства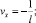 
vN = 0, v0 = 1, получаем
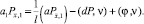(26)
Применяя неравенство Коши – Буняковского [1, 3], оценим по модулю слагаемые в правой части (26):
а)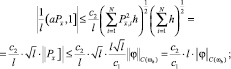 
б)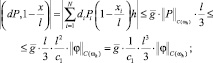 
в)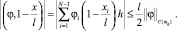 
С учетом полученных оценок и неравенства 
из (26) находим
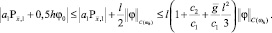(27)
Из (24) и (27) получаем оценку
(28)
Из (12), используя оценки (15), (16) и (28), получаем равномерную оценку решения конечно-разностной схемы (8), (9),
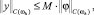(29)
где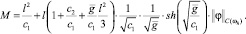 
Из оценки (29) следует устойчивость конечно-разностной схемы (8), (9). Алгоритм решения задачи (8), (9) заключается в решении задач (13) и (14) методом прогонки [3], вычислении yN по формуле (20) и подстановке их в формулу (12). В силу условий на коэффициенты в задачах (13) и (14) метод прогонки при их решении будет устойчивым, погрешность в исходных данных не будет возрастать.
Изложенный выше метод можно использовать для нахождения решения задачи (1), (2) с более высоким порядком точности по шагу h.