Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Рыночная конкуренция – борьба организаций на доступных сегментах рынка за ограниченный объем платежеспособного спроса потребителей.

На первый план в условиях усиления конкуренции для каждой организации выходит задача повышения и сохранения собственной конкурентоспособности.

Конкуренция также может трактоваться и по-другому – это состязание между производителями продукции или другими рыночными, экономическими субъектами; борьба за рынки сбыта товаров с целью получить наиболее высокую прибыль.

Конкуренция представляет собой соперничество субъектов хозяйственной деятельности для достижения более высоких результатов в своих интересах. Она выражает между результатами развития экономики и интересами субъектов хозяйственной деятельности причинно-следственную связь.

В настоящее время на экономическую политику большое влияние оказывают процессы, происходящие в сфере международных финансов. Особенностью международной торговли является то, что она обслуживается разными национальными валютами.

Валютный курс – это цена валюты, которая выражается в валютах других стран, который существенно влияет на внешнюю торговлю и конкурентоспособность национальной продукции на мировом рынке.

Конкуренция на рынке приводит производителей к стремлению снижать собственные производственные затраты для увеличения прибыли. Результатом является повышение производительности, снижение издержек, повышение качества выпускаемого товара и увеличение его разнообразия. Таким образом, производители вынуждены постоянно бороться с конкурентами за покупателей на рынке сбыта путём улучшения и расширения ассортимента высококачественных товаров и услуг, предлагаемых по более низким ценам. Если рассматривать конкуренцию на валютном рынке, то на конкурентоспособность национальной продукции на мировом рынке существенно влияет валютный курс. Изменения валютного курса подразумевают удорожание или обесценивание валюты. При удорожании курса валюты внутренние цены становятся менее конкурентоспособными, эффективность экспорта падает, что может привести к сокращению экспортных отраслей и национального производства в целом. Импорт, наоборот, расширяется. При обесценивании валюты – наоборот. Эти изменения сказываются на конкурирующих организациях на мировом рынке.

Рассмотрим критерии оптимальности для двух конкурирующих организаций «Нова Корп» и «Вива Индастрис» (названия предприятий выдуманы). Обе организации стремятся удержать свои лидирующие позиции на рынке и не уйти в убыток. При этом организации стараются расширить свою долю рынка, закупая акции предприятий, которые не выдерживают конкуренции и прекращают свою деятельность. Всегда существует вероятность того, что курс валюты может измениться. Такие скачки курса валют сказываются на компаниях. При уменьшении курса валюты для крупных организаций выгодно приобретать акции других предприятий или продавать акции при его увеличении.

С каждым днем курс валюты меняется – то увеличивается, то падает. Также бывает, что курс валюты не изменяется, но это крайне редко. Следовательно, изменение курса валюты может выступать в качестве «природы», то есть: П1 – спад курса валюты; П2 – курс валюты не изменяется; П3 – увеличение курса валюты.

В качестве стратегий организации «Нова Корп» (НК) выступают: НК1 – закупать акции; НК2 – продавать акции.

В качестве стратегий организации «Вива Индастрис» (ВИ) выступают: ВИ1 – закупать акции; ВИ2 – продавать акции.

Можно экспертным путем оценить численно последствия применения каждой стратегии соответствующей организации при любом изменении курса валюты, то есть игры могут быть представлены платежными матрицами

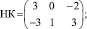
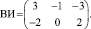
Воспользуемся различными критериями оптимальности для выбора оптимальных стратегий, опираясь на платежные матрицы НК и ВИ и на матрицы рисков. Матрица рисков находится по формуле

rij = βj – aij,

где βj = maxi aij.

Составим матрицы рисков R1, R2 для платежных матриц НК и ВИ соответственно. Для этого сначала рассчитаем βj для каждой матрицы.

Для платежной матрицы НК β1 = maxi ai1 = 3, β2 = maxi ai2 = 1, β3 = maxi ai3 = 3. Следовательно, матрица рисков

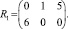
Для платежной матрицы ВИ β1 = maxi ai1 = 3, β2 = maxi ai2 = 0, β3 = maxi ai3 = 2. Следовательно, матрица рисков

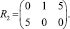
Если известны вероятности pj состояний Пj, то используют критерий принятия решения Байеса. Берется стратегия, при которой максимизируется средний выигрыш 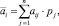то есть

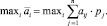
Расчеты наглядно представим в виде таблиц (табл. 1 и 2).

Таблица 1

Нахождение критерия Байеса для НК

Из табл. 1 видно, что 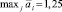, следовательно, по критерию Байеса оптимальной стратегией организации «Нова Корп» является НК2.

Таблица 2

Нахождение критерия Байеса для ВИ

Из табл. 2 видно, что 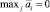, следовательно, по критерию Байеса оптимальной стратегией организации «Вива Индастрис» является ВИ2.

Когда вероятности рj неизвестны, используют следующие критерии оптимальности.

По критерию Вальда оптимальной стратегией будет та, при которой минимальный средний выигрыш будет максимальным, то есть

α = maxi minj aij.

Оптимальной стратегией организации «Нова Корп» по критерию Вальда будет НК1, так как

maxi minj aij = –2 = α1.

А оптимальной стратегией организации «Вива Индастрис» по критерию Вальда будет ВИ2, так как

maxi minj aij = –2 = α1.

Для нахождения оптимальной стратегии по критерию Севиджа в неблагоприятной ситуации величина риска должна принимать минимальное значение, то есть

K = mini maxj rij.

Нахождение критерия Севиджа для НК. По табл. 1 составим матрицу рисков R = {rij} (табл. 3).

Таблица 3

Нахождение критерия Севиджа для НК

Оптимальной стратегией организации «Нова Корп» по критерию Севиджа будет НК1, так как

K = mini maxj rij = 5.

Нахождение критерия Севиджа для ВИ. По табл. 2 составим матрицу рисков R = {rij} (табл. 4).

Таблица 4

Нахождение критерия Севиджа для ВИ

Оптимальной стратегией организации «Вива Индастрис» по критерию Севиджа будут ВИ1 и ВИ2, так как

K = mini maxj rij = 5.

По критерию Гурвица берется значение λ от 0 до 1, чем больше нужно подстраховаться в такой ситуации, тем это значение ближе к единице. Возьмем λ = 0,9 и рассчитаем величину, по которой будем выбирать оптимальную стратегию:

H = maxi {λ minj aij + (1– λ) maxj aij}.

Расчеты наглядно представим в виде таблиц (табл. 5 и 6).

Из табл. 5 видно, что H = maxi hi = –1,5, то есть оптимальной стратегией организации «Нова Корп» является НК1.

Из табл. 6 видно, что

H = maxi hi = –1,6,

то есть оптимальной стратегией организации «Вива Индастрис» является ВИ2.

Из всех рассчитанных критериев можно сделать вывод, что стратегии НК1 и ВИ2 являются оптимальными для двух организаций «Нова Корп» и «Вива Индастрис», так как эти стратегии более выгодные, чем стратегии НК2 и ВИ1. Это значит, что для организации «Нова Корп» выгодно закупать акции других компаний при изменении курса валюты, особенно когда курс идет на спад. А для организации «Вива Индастрис» менее рискованно продавать акции при изменении курса валюты, особенно когда курс увеличивается или не изменяется.

Таблица 5

Нахождение критерия Гурвица для НК

Таблица 6

Нахождение критерия Гурвица для ВИ

Рассмотрим следующий пример. Две крупнейшие промышленные организации – «Нова Корп» и «Вива Индастриз» – находятся в постоянной конкуренции друг с другом. У каждой организации свои методы производства и сбыта товара. Каждая из них занимает приблизительно равную долю на рынке. Из-за сложной экономической ситуации в государстве мелкие и средние предприятия не выдерживают тяжёлых для них условий существования и конкуренции и уходят с рынка. Незначительная часть предприятий перекупается организацией «Нова Корп», а часть – организацией «Вива Индастриз». Так как основная часть мелких предприятий перестаёт существовать, освобождается некоторая часть рынка. В интересах обоих предприятий захватить эту часть рынка, чтобы стать предприятием-лидером. Соответственно, одной из целей обеих компаний является увеличение продаж и максимизация потоков прибыли. Для этого каждая организация использует свои методы достижения целей. Компания «Нова Корп» для достижения этих целей использует два этапа. На первом она может выбрать одну из двух альтернатив:

1. Внедрение инноваций в технологический процесс.

2. Использование инновационных технологий в экономической сфере.

Второй этап является не обязательным. «Нова Корп» разработала его на случай, если компания-конкурент «Вива Индастриз» примет какие-либо ответные действия для достижения поставленных целей. Мероприятия второго этапа представляют из себя:

1. Создание нового продукта.

2. Снижение стоимости производства (что снизит стоимость конечного продукта). Примером может быть закупка более дешёвого сырья.

«Вива Индастриз» не планирует предпринимать активных действий по достижению целей, рассчитывая на качество и привлекательность своих товаров, кроме случая, если компания-конкурент «Нова Корп» первой не предпримет активных действий. В такой ситуации у компании «Вива Индастриз» есть два пути действия:

1. Разработка и выпуск нового вида продукции.

2. Модификация уже имеющихся образцов.

Представим ситуацию в виде позиционной игры. Для удобства введём псевдонимы-обозначения:

А – организация «Нова Корп»;

В – организация «Вива Индастриз».

Первый ход делает игрок А. Он выбирает число х из множества двух чисел {1, 2} (где {1, 2} – альтернативы действий).

Второй ход делает игрок В. Зная выбор игрока А на первом ходе, он выбирает число у из множества двух чисел {1, 2}.

Третий ход делает игрок А. Он выбирает число z из множества двух чисел {1, 2}. При этом он знает выбор у игрока В на втором ходе, и помнит свой выбор х на первом ходе.

После игроки расплачиваются по правилу W(x, y, z). Согласно мнению экспертов, функция выплат игроку А за счёт игрока В задаётся так (все значения указаны в млрд у.е.):

Графическое представление этой игры показано на рисунке.

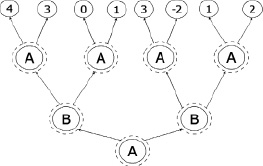
Графическое представление игры

Поскольку игроку В известен выбор игрока А на первом ходе, то он знает, в какой именно из двух возможных позиций он находится. Поэтому у него четыре стратегии:

В1 – [1, 1]; В2 – [1, 2]; В3 – [2, 1]; В4 – [2, 2].

При описании стратегий игрока А следует исходить из того, что ему известен выбор игрока В на втором ходе, и к третьему ходу игрок А знает свой выбор на первом ходе. Поэтому выбор числа z игроку А следует связать с известным ему к третьему ходу значением у. Удобнее всего это сделать при помощи упорядоченной пары: [z1, z2].

Здесь z1 – альтернатива, выбираемая игроком А при условии, что игрок В выбрал первую альтернативу на первом ходе, у = 1, а z2 – альтернатива, выбираемая игроком А при условии, что игрок В выбрал вторую альтернативу, у = 2.

Чистую стратегию игрока А в данной игре можно записать так: (x, [z1, z2]).

Здесь х1 – альтернатива, которую игрок А выбирает на первом ходе, z1 – альтернатива, которую игрок А выбирает на третьем ходе, если на первом ходе игрок В выбрал первую альтернативу (у = 1) и z2 – альтернатива, которую игрок А выбирает на третьем ходе, если на втором ходе игрок В выбрал вторую альтернативу (у = 2).

Таким образом, у игрока А восемь чистых стратегий:

А1 – (1, [1, 1]); А2 – (1, [1, 2]);

А3 – (1, [2, 1]); А4 – (1, [2, 2]);

А5 – (1, [1, 1]); А6 – (1, [1, 2]);

А7 – (1, [2, 1]); А8 – (1, [2, 2]).

Теперь следует показать, как определяются элементы таблицы выигрышей игрока А (в зависимости от применяемых стратегий).

Допустим, что игрок А выбирает стратегию А3 – (1, [2, 1]), а игрок В – стратегию В2 – [1, 2]. Тогда х = 1, из [1, 2] получаем, что у = 1 и из [2, 1] – что z = 2. Отсюда

W(x, y, z) = W(1, 1, 2) = 3.

По аналогии вычисляются и остальные элементы. В результате получаем:

В соответствии с заданной функцией выплат получим следующую матрицу выигрышей игрока А (строки соответствуют стратегиям игрока А, столбцы – стратегиям игрока В):

Исключим из матрицы доминируемые стратегии (такими являются строки p1, p3, p4, p5, p7, p8). Получим

Найдём минимальные значения по строкам. Для строки 1:

min {4, 4, 1, 1} = 1.

Для строки 2:

min {3, 2, 3, 2} = 2.

Теперь находим max из полученных минимумов:

max {1, 2} = 2.

Дальше находим максимальные значения по столбцам.

max {4, 3} = 4; max {4, 2} = 4;

max {1, 3} = 3; max {1, 2} = 2.

Минимальное из этих значений:

min {4, 4, 3, 2} = 2.

Минимальное из максимумов равно максимальному из минимумов, следовательно, матрица имеет седловую точку v = 2.

Таким образом, оба игрока имеют оптимальную стратегию (на пересечении строки 6 и столбца 4, так как полученное значение (цена игры, равная 2) находится именно на этой позиции): для игрока А: А6 – (2, [1, 2]); для игрока В: В4 – [2, 2].

Исходя из этого, игрок А, то есть компания «Нова Корп», выберет вариант х = 2 – использование инновационных технологий в экономической сфере, игрок В («Вива Индастриз») в ответ на действия компании «Нова Корп» выберет вариант у = 2 – модификация уже имеющихся образцов, и уже после этого «Нова Корп», приводя в действие второй этап для достижения целей, выберет вариант z = 2 – снижение стоимости производства.