В настоящее время для изучения процессов, проходящих при затвердевании сплавов, используют комплексный подход, объединяющий в себе целый ряд различных дисциплин: термодинамику, гидродинамику, теорию тепломассопереноса, теорию фазовых превращений, механику деформируемого твердого тела. В проблеме моделирования крупногабаритных слитков можно выделить отдельные, но взаимосвязанные процессы: гидродинамическая задача течения расплава, сопровождающаяся тепломассопереносом; задача описания процессов формирования кристаллической структуры отливки и усадочной пористости; исследование процесса охлаждения закристаллизовавшегося слитка до заданной температуры, задача описания теплообмена между слитком, формой и окружающей средой. Для решения каждой из упомянутых задач существует ряд подходов и методов, но только комплексное использование полной математической модели процесса изготовления отливки может дать достоверную и надежную информацию о качестве будущего изделия.
Численному моделированию процесса кристаллизации слитков посвящено множество работ. Первые попытки описать поведение металлов в процессе заливки и кристаллизации появились более шестидесяти лет назад [14]. Сейчас для изучения процессов, проходящих при затвердевании сплавов, все чаще используется комплексный подход, т.е. совместное решение задач термодинамики и гидродинамики, также учитывают влияние тепломассопереноса, фазовые превращения [1, 8]. В основе моделирования заполнения формы расплавом лежат уравнения движения жидкости, уравнения тепломассопереноса, диффузии, кинетическое уравнение фазовых превращений [4, 7]. Течение расплава может рассматриваться как в ламинарной [2], так и в турбулентной постановке [11]. Среди задач вычислительной гидродинамики особенную сложность и практический интерес представляют задачи моделирования течений вязкой жидкости с подвижными границами [6].
При моделировании процесса изготовления слитков важно учесть тепловое взаимодействие между всеми компонентами литейной установки. В настоящее время условия теплообмена между элементами литниковой установки чаще всего принимают контактными, либо частично контактными, с учетом зазора между кристаллизующейся отливкой и формой [3]. В работе [10] в двумерной постановке решена задача кристаллизации бинарного сплава, затвердевающего в цилиндрической металлической форме. Для переходной твердожидкой зоны в интервале температур фазового перехода использована равновесная модель. Конвективным потоком расплавленного металла в данной модели пренебрегли. В статьях [9, 12] представлены результаты оптимизации конструкции изложницы при изготовлении массивного слитка. В [5] использовалась трехмерная модель крупного слитка массой 142 т. Отмечено влияние свободной конвекции на температурные поля в расплаве и качество литой структуры.
Несмотря на актуальность решения задач литейных процессов, численное моделирование процесса кристаллизации крупногабаритных изделий занимает значительное время и требует наличия высокопроизводительных вычислительных систем. Поэтому вопрос экономии вычислительных ресурсов выходит на первый план. Для этого необходимо выделить те процессы, моделированием которых можно пренебречь без существенной потери точности прогнозирования интересующих величин. В данной работе исследуется процесс кристаллизации с учетом и без учета естественной конвекции расплава в процессе затвердевания.
Описание объекта исследования и концептуальная модель
Объектом исследования является слиток массой 10 тонн, который отливают из конструкционной стали в форму из серого чугуна. Геометрические характеристики слитка: отношение высоты к диаметру 3,4; конусность слитка на одну сторону 7 %; характерные размеры слитка: нижний диаметр 760 мм, верхний диаметр 890 мм, высота слитка с прибыльной частью 1980 мм. Температура окружающей среды 20 °С, форма предварительно разогрета до 50 °С. Температура заливки составляет 1585 °С, полное время заливки – 9 минут 30 секунд. В рассматриваемом производстве разливка производится сифонным способом, что позволяет одновременно заполнять металлическим расплавом две изложницы. Для экономии вычислительных ресурсов рассматривается половина всей системы: одна изложница со слитком и половина литниковой системы (рис. 1).
Численная модель процессов, протекающих при заливке и кристаллизации слитка, построена в конечноэлементной среде ProCast. Рассмотрены два расчетных варианта. В первом варианте заливка смоделирована с помощью задания источника с заданным массовым расходом на поверхности центровой литниковой системы. Сначала описан гидродинамический режим заполнения формы с учетом турбулентности: циркуляция жидкого металла и температурное поле на форме и слитке на момент окончания заливки; затем проведен анализ условий теплообмена при дальнейшем охлаждении слитка в форме с учетом естественной конвекции расплава.
Во втором варианте смоделирован гидродинамический режим заполнения формы с учетом турбулентности: циркуляция жидкого металла и температурное поле на форме и слитке на момент окончания заливки; затем проведен анализ условий теплообмена при дальнейшем охлаждении слитка в форме без учета естественной конвекции расплава.
Обе модели строятся в следующих предположениях:
? использована стандартная κ–ε модель турбулентности [13];
? используется гравитационная модель течения со свободной поверхностью;
? система находится в поле силы тяжести и никакие другие внешние силы на нее не действуют;
? кристаллизация описывается в рамках равновесной теории двухфазной зоны, сплав бинарный, сегрегация не рассматривается;
? выделение тепла при твердофазных изменениях не учитывается, а учитывается только выделение скрытой теплоты при переходе из жидкой в твердую фазу;
? тепловой контакт «поддон ? форма», «форма ? прибыльная наставка» идеальный.
Условия охлаждения на границе «форма ? окружающая среда» задавались в виде комбинации конвективного и лучистого теплообмена. На границах «отливка ? форма», «отливка ? вкладыш» при жидкой фазе отливки задается конвективный теплообмен, при переходе из жидкой фазы отливки в твердую на указанных границах задается кондуктивный теплообмен. На границе «вкладыш ? форма» – задается кондуктивный теплообмен.
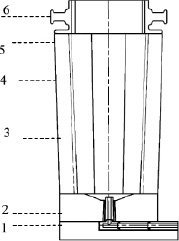
Рис. 1. Схема слитка с расположением контрольных точек для экспериментального измерения температуры на поверхности формы
Результаты численного исследования заливки и процесса кристаллизации
На рис. 2 приведено распределение скоростей и картина циркуляции расплава в процессе заливки расплава. Видно, что распределение несимметрично вследствие того, что в модели учтена не только изложница, но и литниковая система, из которой расплав поступает в изложницу с нарушением осевой симметрии течения. Указанное явление приводит к тому, что фронт кристаллизации также реализуется несимметрично.
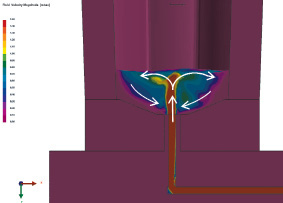
Рис. 2. Распределение скоростей [м/с] и картина циркуляции расплава в процессе заливки (t = 56 с)
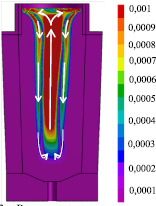
Рис. 3. Распределение скоростей [м/с] и картина циркуляции расплава в затвердевающем слитке (t = 30 мин)
На рис. 3 представлены распределение скоростей и картина циркуляции расплава в процессе затвердевания слитка. Видно конвективное движение в жидком ядре слитка относительно твердой фазы. Проведение данного расчета на персональном компьютере, в выполнении которого было задействовано 8,5 млн конечных элементов, заняло около 160 часов. Время расчета без учета естественной конвекции (также 8,5 млн элементов) составило 16 часов. Температурные поля ко времени окончания заливки идентичны, однако при дальнейшей кристаллизации в модели без учета конвекции теплоотвод в зоне прибыльной части слитка идет интенсивнее.
В модели без учета естественной конвекции кристаллизация идет неравномерно, с образованием замкнутых полостей с жидким ядром, в модели же с учетом естественной конвекции такое явление отсутствует. Однако толщина корки, образующейся на поверхности изложницы, на протяжении всего процесса кристаллизации практически одинакова, значительные отличия наблюдаются только в прибыльной части. Это можно объяснить отсутствием подпитки в этой зоне более горячим расплавом. Также значительно отличается время полной кристаллизации, но основное тело слитка кристаллизуется в одинаковых временных интервалах.
Таким образом, модель без учета конвекции позволяет адекватно оценить процессы, происходящие в основном теле слитка, но не отражает в полной мере процессы в прибыльной части слитка, при этом данный расчет занимает на порядок меньше времени. На рис. 6 приведено сравнение результатов расчета в виде зависимости доли затвердевшей части слитка от времени (рис. 6, а) и средней температуры слитка от времени (рис. 6, б). По приведенным интегральным параметрам расхождение незначительно и лежит в пределах 2–3 %.
Средствами пакета ProCast по результатам решения тепловой и гидродинамической задач имеется возможность оценить закономерности формирования пористости в теле слитка. В решении без учета конвекции пористость в пределах 1–2 % сосредоточена вдоль наружной поверхности слитка, толщина зоны с пористостью составляет 7,88 см на расстоянии 60 см от основания изложницы (слитка), 6,04 см на расстоянии 125 см от основания изложницы (слитка), 5,40 см на расстоянии 120 см от основания изложницы (слитка). В решении c учетом конвекции расплава – пористость в пределах 1–2 % равномерно распределена по всему слитку.
|
Без учета конвекции |
С учетом конвекции |
|
|
Через 15 минут после начала заливки |
|
|
|
Через 2 часа 5 минут после начала заливки |
|
|
Рис. 4. Доля твердой фазы в процессе разливки и кристаллизации
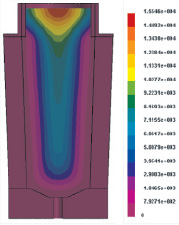
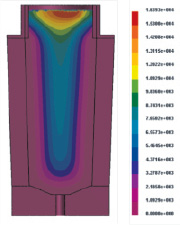
а б
Рис. 5. Время кристаллизации слитка: а – без учета конвекции 4 часа 19 минут (15546 с); б – с учетом конвекции 4 часа 42 минуты (16948 с)
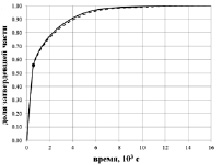
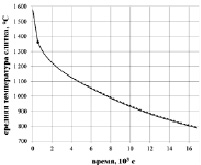
а б
Рис. 6. Доля затвердевшей части слитка (а) и среднеобъемная температура слитка (б) для различных вариантов расчетов: – – – модель с учетом конвекции; —– – модель без учета конвекции
Для верификации расчетов было проведено сравнение результатов моделирования с результатами экспериментального измерения температуры на наружной поверхности формы в процессе разливки и кристаллизации в четырех различных точках (рис. 1).
На рис. 7 представлены результаты экспериментального измерения и численного решения задачи, с учетом естественной конвекции расплава и без, в четырех различных точках. Из сравнительного анализа можно сделать вывод о том, что математическая модель, учитывающая естественную конвекцию расплава, лучше отражает процессы, проходящие в процессе разливки и кристаллизации крупногабаритного слитка. Расхождение значений температур на этапе разливки можно объяснить как наличием технологических зазоров в изложнице, которые не учитываются в моделях, так и неравномерным фактическим распределением начальной температуры по толщине стенок изложницы, в то время как в численных расчетах начальная температура принималась постоянной.
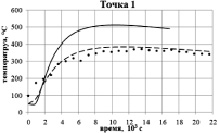
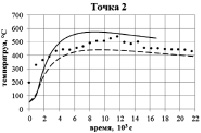
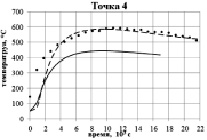
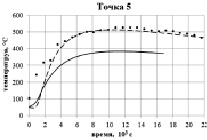
Рис. 7. Сравнение температур, полученных численно и экспериментально замеренных, в контрольных точках на наружной поверхности формы: ••• – эксперимент; – – – модель с учетом конвекции; —– – модель без учета конвекции
В нижней части изложницы модель без учета конвекции дает завышенные значения температуры, а в верхней – ниже реально замеренных. Фактическое время полной кристаллизации слитка практически совпадает с расчетными значениями, что говорит о корректности предложенного подхода для моделирования разливки и кристаллизации крупногабаритных слитков.
Заключение
Несмотря на незначительные отличия в общей оценке между двумя моделями, температура на поверхности изложницы в модели без учета естественной конвекции значительно ниже реальных в верхней части слитка и выше реальных значений в нижней части. Таким образом, модель, учитывающая естественную конвекцию расплава, является адекватной и в достаточной мере отражает тепловые и гидродинамические процессы, протекающие в ходе заливки и затвердевания крупногабаритного слитка. При этом модель, не учитывающая естественную конвекцию, может быть рекомендована для оценки в достаточно краткие сроки времени полного затвердевания слитка и получения первого приближения при решении температурной задачи.
Работа выполнена при финансовой поддержке Министерства образования и науки РФ (договор № 02.G25.31.0068 от 23.05.2013 г. в составе мероприятия по реализации постановления Правительства РФ № 218).