Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

В статье приведены результаты экспериментальных исследований по распознаванию отдельных реальных плоских объектов (ОРПО) с использованием безразмерных признаков, полученных из характеристик контуров бинарных изображений этих объектов, разработанных в [14].

Распознавание объектов по их изображениям – традиционная область цифровой обработки изображений. Распознавание имеет своей целью отнесение объекта к одному из заранее предопределенных типов. Для решения данной задачи необходимо получение определенных признаков объекта по его изображению, которые позволят идентифицировать его с минимальной ошибкой. Для установления связи между значениями признаков объекта и решения о принадлежности его к определенному классу необходимо использование обучающей совокупности известных объектов [1–13].

Общая технология проведения экспериментов расчета безразмерных признаков по контурам бинарных изображений отдельных тестовых плоских объектов и их распознавания состоит из получения контура изображения объекта, вычисления признаков, обучения системы.

На рис. 1 приведены 10 исходных изображений ОРПО.

Эксперимент проводится на презентабельной выборке изображений каждого из 10 ОРПО. Для этого проводится генерация множества повернутых изображений.

Предварительно выполняется линейная фильтрация входного изображения и удаление фона. Выходом этапа является изображение реального объекта на белом фоне.

Для каждого из сгенерированных изображений вычисляются центры тяжести.

Для вращения изображения на угол α используется алгоритм, приведенный в [7].

Рис. 1. Тестовые изображения

Формируется массив повернутых изображений каждого из 10 ОРПО с шагом в 1 градус. Всего 3600 изображений.

Далее реализуется имитация случайного появления объекта в поле зрения распознающей системы. С помощью генераторов случайных чисел (ГСЧ) с нормальным распределением из повернутых 360 изображений каждого из 10 ОРПО формируется 10 массивов по 2000 изображений.

С помощью второго ГСЧ получаем числа в диапазоне 0,364 до 0,720. Такое ограничение необходимо для того, чтобы свести к минимуму расположения изображений вне рабочего поля). Для 2000 реализаций каждого объекта генерируются 4000 чисел. Первое число от ГСЧ будем считать координатой центра тяжести по оси икс Хц объекта, второе число – Yц. Таким образом определяются координаты центра тяжести каждой из 2000 реализаций каждого из 10 ОРПО. Согласно этим координатам 2000 реализаций каждого из 10 ОРПО размещаются на рабочем поле.

Выполняется бинаризация полутоновых изображений с использованием алгоритма сегментации Отсу.

По полученным изображениям рассчитывается количество точек в каждой из 2000 реализаций каждого из 10 ОРПО, то есть вычисляет площадь объекта S0. Формируются одноточечные контуры бинарных изображений объектов по алгоритму в [3].

Рассчитывается количество точек P0, образующих контур каждой из 2000 реализаций каждого из 10 ОРПО. Определяется метрическая длина Lконт контура каждой из 2000 реализаций каждого из 10 ОРПО.

Определяется значение кривизны в точках каждого контура каждой из 2000 реализаций каждого из 10 ОРПО, а также маркируются опорные точки выпуклых и вогнутых участков контура по алгоритму в [8].

По полученным изображениям вычисляется количество опорных точек выпуклых, вогнутых и линейных участков контуров:

М1 – количество точек контура со значением +90;

М2 – количество точек контура со значением –90;

М3 – количество точек контура со значением +135;

М4 – количество точек контура со значением –135;

К – количество 4-х связных точек контура;

Т – количество D связных точек контура.

По формулам (1), (2) и (3) вычисляем общую длину выпуклых, вогнутых и линейных участков всего контура каждого объекта:

Lобщ.вып = 1/2[М12b + М3(а + b)]; (1)

Lобщ.вог = 1/2[М22b + М4(а + b)]; (2)

Lобщ.лин = 1/2(К2а + T2b), (3)

где a – расстояние между 4 связными точками; b – расстояние между D связными точками.

По полученным осуществляем расчет векторов безразмерных признаков каждой из 2000 реализаций всех 10 ОРПО.

К1 = Po/S0; (4)

К2 = М1/S0; (5)

К3 = М2/S0; (6)

К4 = М3/S0; (7)

К5 = М4/S0; (8)

К6 = К/S0; (9)

К7 = Т/S0; (10)

К8 = М1/P0; (11)

К9 = М2/P0; (12)

К10 = М3/P0; (13)

К11 = М4/P0; (14)

К12 = К/P0; (15)

К13 = S0/P0; (16)

К14 = Lобщ.лин/Lконт; (17)

К15 = Lобщ.вог/Lконт; (18)

К16 = Lобщ.вып/Lконт. (19)

Далее в диалоговом режиме осуществляется выбор эталонов для распознавания каждой из 2000 реализаций каждого из 10 ОРПО. По гистограмме, полученной на этапе генерации, выбирается вектор признаков самой часто использованной из 360 повернутых вариантов, например 1-го ОРПО, при формировании 2000 реализаций. Для данного вектора коэффициентов по методу среднеквадратичного отклонения (20) вычисляется Zi с каждой из 2000 реализаций.

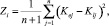(20)

где n – число признаков; l – номер распознаваемого объекта (l = 1, 2, …, 2000); Кej – значение j-го признака вектора коэффициентов К выбранного эталона; Кlj – значение j-го признака вектора коэффициентов К выбранной реализации.

Вычисляются 2000 СКО Zi. Среди них ищутся Zmin:

Zmin = min{Zi}. (21)

Найденные значения Zmin указывают номера реализаций среди 2000 изображений, вектора-признаки которых совпадают с вектором-признаком выбранной как эталон реализации. Очевидно, что с одним эталоном распознать все 2000 реализаций 1-го ОРПО невозможно.

На втором шаге на основе гистограммы выбирается как эталон вектор-признак следующей часто использованной из 360 повернутых вариантов, например 1-го ОРПО, при формировании 2000 реализаций. Вычисляются 2000 СКО Zi. Среди них ищутся Zmin по формуле (21).

Найденные значения Zmin указывают номера реализаций среди 2000 изображений, вектора-признаки которых совпадают с вектором-признаком выбранной как эталон реализации и т.д. Выбор эталонов для реализаций 1-го ОРПО проводится до тех пор, пока не будут распознаны все 2000 реализаций.

Аналогично, выбор эталонов проводится для всех реализаций всех остальных 9 ОРПО.

Результаты выбора эталонов для 2000 реализаций каждого из 10 ОРПО приведены в табл. 1.

На этом обучение системы распознавания завершается.

Экзамен обученной системы осуществляется на 20000 реализациях всех 10 ОРПО на основе формул (20) и (21).

Экзамен заключается в сравнении векторов признаков всех 20000 реализаций всех 10 ОРПО с выбранными эталонами.

Производится выбор некоторого случайного объекта. Для него выполняются все описанные процедуры получения безразмерных признаков контура. Полученный вектор признаков неизвестного ОРПО сравнивается со всеми эталонными векторами-признаками в табл. 2. Определяется тип ОРПО в соответствии с min{Zmin}.

Процедура экзамена повторяется для 2-го неизвестного объекта и так далее для всех 20000 реализаций всех 10 ОРПО. Строится таблица правильного распознавания.

Таблица 1

Таблица 2

Результаты правильной идентификации всех реальных объектов при количестве эталонов от 10 до 48 на каждый объект

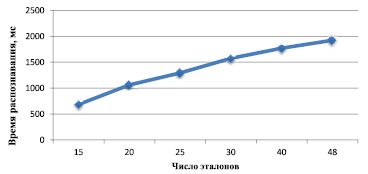
Рис. 2. График зависимости времени распознавания от числа эталонов на объект

График изменения времени на распознавание при увеличении количества эталонов представлен на рис. 2.

Заключение

Объект под номером 3 имеет простой контур. Но вследствии дискретного характера значения координат точек, составляющих изображение, при вращении меняется структура контура. При некоторых углах имеет место большее количество линейных участков контура изображения данного объекта. При этом при других углах линейный характер контура изменяется, и получаем большое количество выпуклых участков с углом 135. Вследствие этого первичные коэффициенты различных повернутых экземпляров данного объекта существенно отличаются. А значит, и полученные векторы признаков будут иметь отличия. На этапе обучения одним эталоном удается распознать меньшее количество изображений. Это привело к необходимости использовать 48 эталонов для достижения 100-процентного распознавания.

Те же рассуждения справедливы и для объекта 5. При вращении полутонового изображения получаем различное соотношение линейных, выпуклых и вогнутых участков контура.

При обучении системы для распознавания объекта под номером 4 получено 19 эталонов. При всей сложности изображения исходного объекта его бинаризованное представление дало небольшое различие в векторах признаков.

В ходе проведения экспериментов получено время, требуемое для распознавания поступающего на вход тестовой системы изображения объекта. Используемая для написания программа не подвергалась оптимизации, в результате чего полученное время является достаточно большим для применения в системах технического времени. Основное время занимают алгоритмы выделения одноточечного контура и маркировки опорных точек. При практическом использовании данного алгоритма идентификации объектов необходимо провести оптимизацию данных функций в программе. Также в программе используются линейная фильтрация и алгоритм бинаризации Отсу. Данные алгоритмы широко применяются в различных задачах цифровой обработки изображений, и возможно использование готовых функций, оптимизированных для применения в системах реального времени.