В настоящее время основой использования методов синтеза виртуальной реальности для проектирования МОП-транзисторов являются процессы и методы формирования 3D моделей в виде структурных решёток материалов тех слоёв, из которых формируются транзисторы, а также определение связей между параметрами материалов с электрическими параметрами электронной компонентной базы [1–14].
Поэтому целью исследования являются модели МОП-транзисторов для САПР на основе применения методов синтеза виртуальной реальности в виде отдельных слоёв.
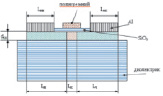
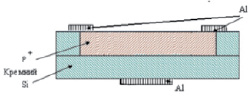
Ввиду этого для построения 3D моделей любых проектируемых транзисторов необходимо опираться на особенности их структур. Так, например, имеются следующие структуры транзисторов: биполярные, планарные, КНИ или КНС, полевые транзисторы с управляющим p-n-переходом, полевые транзисторы с изолированным затвором и с индуцированным каналом, полевые транзисторы с изолированным затвором и со встроенным каналом. Структуры МОП-транзисторов обладают характеристиками, позволяющими создавать электронную компонентную базу с широкими возможностями по мощности. К ним относятся структуры: n-МОП КНД (кристалл на диэлектрике) – транзисторы и МОП-транзисторы (рис. 1). В связи с этим данная статья посвящена моделированию именно таких транзисторов.
а б
Рис. 1. Структуры транзисторов: а – n-МОП КНД; б – МОП
Опираясь на исследования в работах [1–14], видим, что для 3D моделирования необходимо знать геометрические параметры транзисторов, материалы отдельных слоев транзисторов, связь геометрических и электрических параметров транзисторов.
Каждый из материалов МОП-транзистора имеет свою структуру кристаллической решётки. К ним относятся: модель элементарной ячейки триклинной сингонии; модель элементарной ячейки моноклинной сингонии; модель элементарной ячейки орторомбической сингонии; модель элементарной ячейки тетрагональной сингонии; модель элементарной ячейки кубической сингонии; модель элементарной ячейки гексагональной сингонии. Из данных моделей видно, что основой задания кристаллических решёток являются длина (а), ширина (b) и высота (c) ячейки. Кроме того, расположения атомов кристаллической решётки определяются углами альфа (a) между ребром а и с, бета (b) между углом b и с, и гамма (g) между а и b.
Следовательно, для учёта характеристик материалов при формировании 3D моделей предлагается ввести в программный модуль таблицу с видом и названием кристаллических структур у имеющихся материалов. Тогда, опираясь на данные такой таблицы, можно выбирать основные параметры, определяющие формирование кристаллических решёток в виде 3D моделей. К ним относятся значения постоянной периода кристаллической решётки и радиусы атомов или ядер. Также следует учитывать, что вид кристаллической решётки полупроводников обладает равноценными связями в любом тетраэдрическом направлении.
Для упрощения формирования кристаллических решёток с использованием методов синтеза виртуальной реальности в данных исследованиях предлагается учитывать индексы Миллера (например, если в дальнейшем потребуется оценивать эффект ионизации от воздействий рентгеновского излучения). В этом случае должна учитываться ориентация атомных плоскостей в трёхмерном пространстве. В этом случае кристаллографические индексы будут определять число равных частей, на которые делятся ребра элементарной ячейки, и описываться тремя целыми числами (0 или 1) в виде индексов hkl.
Между индексами (hkl), величиной dhkl и периодами решетки a, b, c существует математическая зависимость. Следует отметить, что для каждой сингонии эта зависимость может быть представлена своим уравнением (1)–(7), соответственно для кубической, тетрагональной, ромбической, гексагональной, тригональной, моноклинной и триклинной ячеек.
В данном случае при формировании 3D модели транзистора предполагается, что величина dhkl определяет толщину между слоями кристаллической решётки или период решётки относительно направления внешних воздействий.
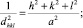 (1)
(1)
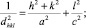 (2)
(2)
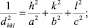 (3)
(3)
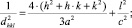 (4)
(4)
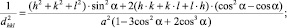 (5)
(5)
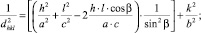 (6)
(6)
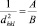 , (7)
, (7)
где 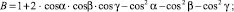
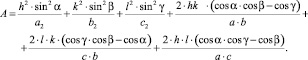
Кроме того введён критерий правильности расчета периодов элементарной ячейки, который базируется на числе формульных единиц, определяемом по формулам (8) (для системы размерности СИ) и (9):
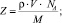 (8)
(8)
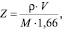 (9)
(9)
где r – плотность вещества (г/см3); V – объем элементарной ячейки (Å3); М – молярная масса вещества (г/моль).
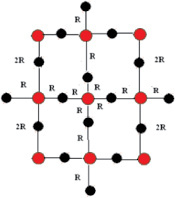
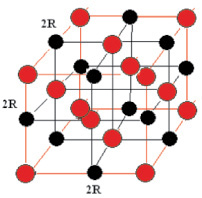
Для данной работы приведён пример преобразования 2D структуры диоксида кремния в структуру 3D. В этом случае было учтено то, что диоксид кремния кристаллизуется в кубической сингонии с параметром гранецентрированной элементарной ячейки а = 5,431 Å (a = b = c). Структура диоксида кремния аналогична структуре, представленной на рис. 2.
Исходя из того, что двумерное представление диоксида кремния (на рисунке слева) имеет такого рода, структуру, то при синтезе виртуальной реальности в 3D виде она формируется в кристаллическую решётку (на рисунке справа). Причем a = b = c = 2R, и более крупными кружками (сферами) обозначен кремний Si.
Таким образом, для создания 3D модели любого транзистора, включая МОП-транзистор, необходимо определить количество слоёв, из которых он состоит. Причём слои материалов и слои 3D модели отличаются друг от друга с целью упрощения формирования этих слоёв.
Примеры проектирования различных геометрических размеров транзисторов с помощью объектно-ориентированного языка программирования CodeGear RAD Studio с использованием компонента Draw3D представлены на рис. 3.
Данная разработанная 3D модель МОП – транзистора представлена в виде отдельного объекта со своими свойствами, которые определяют параметры транзистора.
а б
Рис. 2. Преобразование 2D структуры диоксида кремния SiO2 (а) в структуру 3D (б)
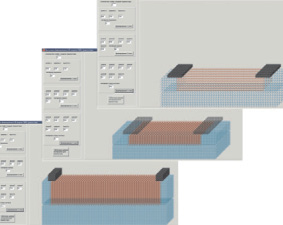
Рис. 3. Примеры проектирования различных геометрических размеров транзисторов с помощью объектно-ориентированного языка программирования CodeGear RAD Studio с использованием компонента Draw3D
Исходя из того, что одним из базовых подходов в проектировании транзисторов является анализируемая структура с тестовыми параметрами, которые и определяют её особенности, то применительно к 3D модели МОП-транзистора выполняется соответствие её свойств с физическими параметрами, такими как толщина dсл [мкм] и уровни легирования приборного слоя [см–3], ширина Wк [мкм] и длина Lк [мкм] канала, длины истока Lи [мкм] и стока Lс [мкм], длина контакта металлизации к истоку Lми [мкм] и к стоку Lмс [мкм], уровни легирования областей стока и истока [см–3], исходные подвижности электронов и дырок [В/(см?с2)], а также исходные времена жизни электронов и дырок [нс]. Входными переменными 3D модели МОП-транзистора являются длина (L) [м] и ширина (W) [м] канала, число параллельных устройств (M или NP), число последовательных устройств (N или NS). К внутренним параметрам 3D модели относятся: затвор окисла ёмкости на единицу площади COX [Ф/м2], глубина залегания перехода XJ [м], ширина канала коррекции DW [м] и длина канала коррекции DL [м], которые имеют отрицательные значения, а также: пороговое напряжение канала VTO [В], параметр трёхмерного геометрического объекта GAMMA [√В], потенциал Ферми подложки PHI [В], параметр активной межэлектродной проводимости KP [A/В2], мобильный поправочный коэффициент E0 [В/м], продольное критическое поле UCRIT [В/м].
Заключение
Таким образом, опираясь на математические зависимости между указанными параметрами 3D модели для МОП-транзистора, можно рассчитать его электрические параметры.
Разработанные с помощью объектно-ориентированного языка программирования CodeGear RAD Studio с использованием компонента Draw3D, модели МОП-транзисторов демонстрируют возможность использования синтеза виртуальной реальности объектов проектирования с целью дальнейшей оценки электрических, физических, химических и энергетических параметров электронной компонентной базы.
Кроме того, данные модели подтверждают возможность 3D моделирования структур в виде отдельных элементов электронной компонентной базы.



