Как известно, климат планеты формируется в земной атмосфере. Особую роль в создании погоды играет тропосфера, представляющая собой ее нижний слой, поскольку в тропосфере сосредоточено более 0,8 всей массы атмосферного воздуха. Здесь наблюдается сильно развитая турбуленция и конвекция, сосредоточена основная часть водяного пара, возникают облака, циклоны и антициклоны [1, 4].
Для исследования нижних слоев атмосферы (тропосферы) применяются различные методы: космический мониторинг, наземная радиолокация, авиационная разведка погоды, применение мобильных метеозондов и дронов.
Особую актуальность приобретают исследования окружающей среды в связи с угрозой «парникового эффекта». Важно получить адекватные результаты анализа химического состава воздушных масс на различных широтах Земли в широком интервале высот.
Наибольший интерес вызывает динамика изменения концентрации углекислого газа (CO2), соединений серы, пылевых выбросов и т.п., не менее важно изучить характер возникновения и изменения озонных дыр. В данном случае шары-зонды при изучении верхних слоев тропосферы имеют ряд преимуществ по сравнению с винтовыми дронами, которые обладают ограниченным ресурсом по высоте к времени пребывания на исследуемых горизонтах.
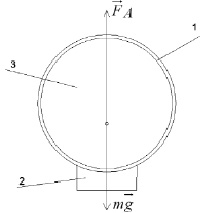
Рис. 1. Схема метеозонда: 1 – оболочка; 2 – аппаратура; 3 – газ
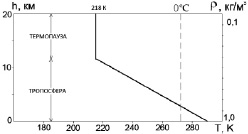
Рис. 2. Распределение температуры по вертикали в атмосфере
В последнее время проводятся эксперименты по применению шаров-зондов для ретрансляции телекоммуникационной информации. Здесь используются специальные приспособления, стабилизирующие траекторию движения шаров-зондов.
Простейший метеозонд имеет, как правило, эластичную оболочку из резины, которая наполняется гелием или водородом (рис. 1). К зонду крепится измерительная аппаратура и средство передачи данных.
В работе [5] было проведено исследование формообразования метеозонда при подъеме в верхние слои тропосферы (рис. 2).
В итоге на основе закона Архимеда была получена формула
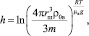 (1)
(1)
где h – наибольшая высота подъема зонда, м; Т – абсолютная температура воздуха на высоте h, K; rш – радиус шара-зонда на высоте подъема зонда h, м; ρ0в – плотность воздуха на поверхности Земли, кг/м3; m – масса шара-зонда (m = mоб + mг – суммарная масса оболочки шара и газа-наполнителя), кг; R = 8,31 Дж/(моль?град) – универсальная газовая постоянная; μв – молекулярная масса воздуха, кг/моль; g ≈ 9,81 м/с2 – ускорение свободного падения у поверхности Земли.
Важно то, что g практически не меняется и на высоте 8–18 км.
Следует отметить, что относительная упругая деформация каучуков (различных видов резины, эластомеров) Е может превышать 100 %. Первоначально при растяжении цепей молекул материала зонда требуется низкое напряжение. По мере растяжения цепей молекул сопротивление дальнейшему деформированию возрастает, так как увеличение деформаций вызывает разрыв связей уже растянутых молекул. Это отображено на диаграмме деформаций (рис. 3).
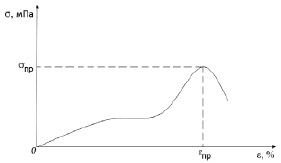
Рис. 3. Схема диаграммы деформаций ε эластомеров от напряжения σ
Исследуем динамику изменения размеров метеозонда в момент его динамического равновесия в верхних слоях атмосферы.
Согласно [2], упругая деформация Е эластомеров (каучуков) может превышать 100 %. На первом этапе деформации для распрямления цепей молекул требуется сравнительно низкое механическое напряжение σ. По мере распрямления цепей молекул сопротивление деформации возрастает, так как это нарастание вызывает разрыв связей уже выпрямленных молекул. Существует предельное значение относительных деформаций Епр, которому соответствует предельная прочность σпр разрушения материала зонда, которая соответствует теоретической прочности σТ.
Определим теоретическую прочность σТ материала зонда (резины, пластика и т.п.) на основании уравнения Орована ? Келли [3]:
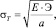 (2)
(2)
где E ≤ 0,02 ГПа = 2?107 Па = 20 МПа – модуль упругости резины;
a = 2?10–8 см = 2?10–10 м – межатомное расстояние в молекулярных цепях резины; Э – удельная поверхностная энергия резинового шара, Дж/м3
Если учесть, что поверхностная энергия Wпов пропорциональна поверхности шара Sш, имеем:
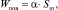 (3)
(3)
где α = const, Дж/м2.
Но удельная поверхностная энергия Э определяется по формуле
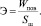 (4)
(4)
Подставляя (3) в (4), получим
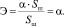 (5)
(5)
Известно, что α зависит от материала оболочки шара.
Подставляя (4) в (2), имеем
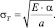 (6)
(6)
Рассмотрим условие разрыва оболочки шара-зонда на предельной высоте подъема h:
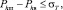 (7)
(7)
где Phш – давление газа-наполнителя на высоте h, Па; Phв – давление воздуха, окружающего шар-зонд, на высоте h, Па.
На основании формулы Менделеева – Клапейрона получим Phш:
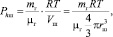 (8)
(8)
где Vш – объем шара-зонда на высоте h, м3.
Опираясь на барометрическую формулу, определим Phв:
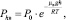 (9)
(9)
где Р0 – давление воздуха, окружающего шар-зонд на поверхности Земли, Па; μв – молекулярная масса воздуха, кг/моль.
Подставляя (1) в (9), имеем
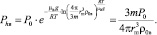 (10)
(10)
Подставляя (6), (8), (10) в (7), получим
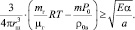 (11)
(11)
Из условия (11) следует предельное значение радиуса шара-зонда на высоте h при температуре Т (рис. 4):
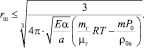 (12)
(12)
Из (12) следует, что rш > 0. Тогда получим температурный режим, при котором не произойдет разрыв оболочки шара-зонда:
 (13)
(13)
тогда имеем
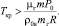 (14)
(14)
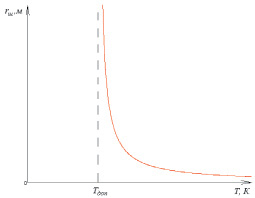
Рис. 4. Зависимость радиуса метеозонда rш от температуры Т тропосферы
Таким образом, в статье:
1. Получена формула (12) предельного значения радиуса резинового шара-зонда на максимальной высоте подъема h при данной температуре тропосферы Т.
2. Получена формула (10) давления Phв воздуха, окружающего шар-зонд, на максимальной высоте подъема h.
3. Установлена допустимая предельная температура Ткр тропосферы (14) на данной высоте h, выше которой происходит разрыв оболочки шара-зонда.



