Адгезию стальных поверхностей принято описывать с точки зрения сил дисперсионного взаимодействия. Многие существующие модели адгезии не учитывают взаимодействие молекул внутри твердого тела и наличие неровностей на поверхностях деталей. Предложенная модель базируется на модели парного взаимодействия молекул, приведенной в работе [4]. В процессе трения детали машин подвержены адгезионному износу. Причем в целом величина адгезионного износа напрямую зависит от числа циклов (nц) взаимодействий поверхностей. Определению адгезионного износа при единичном контакте поверхностей (nц = 1) посвящена настоящая работа.
В процессе трения контактирующие выступы нанонеровностей претерпевают как упругие, так и пластические деформации, при этом часть из них также подвергается срезу (рис. 1) [5].
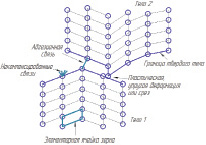
Молекулы твердых тел, оказавшиеся в результате сближения поверхностей на компенсированном расстоянии, на котором энергия взаимодействия равна нулю Fприт = Fотт, образуют адгезионную связь Fвз.
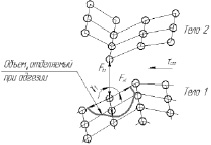
Предположим, что адгезионная связь образовалась на некотором отдалении от места деформации и деформация не оказывает влияния на адгезионную составляющую. Примем, что тело 2 обладает максимально возможной силой межмолекулярного взаимодействия Fм.2 ⇒ max и адгезионный износ данного тела невозможен. Тогда при приложении к телу 2 сдвиговой нагрузки произойдет адгезионный износ тела 1, который представляет собой вырывы на поверхности (рис. 1).
а б
Рис. 1. Молекулярное взаимодействие поверхностей при трении: а – образование адгезионной связи при пластическом контакте; б – вырывы при адгезии поверхностей
а б в
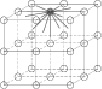
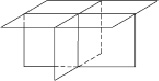
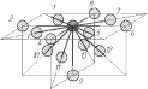
Рис. 2. Структура аустенитной стали: а – объемная структура; б – плоскости расположения соседних молекул; в – расположение соседних молекул
Предположим, что объем единичного адгезионного вырыва определяется силой взаимодействия молекул в теле Fм. Тогда требуется определить векторы l, формирующие объем вырыва. Для тела, имеющего кристаллическую структуру, направление векторов можно определить из формы элементарной ячейки, а величина векторов определяется взаимодействием соседних молекул по выбранному направлению. Например, для стали, основной структурой которой является аустенит, и с учетом того, что адгезионная связь образуется на отдалении от границы зерна, направления и число векторов, определяющих объем вырыва, приведены на рис. 2, а.
Таким образом, векторы, определяющие объем единичного вырыва, расположены в трех взаимно перпендикулярных плоскостях (рис. 2, б), угол между которыми 90°. Задача определения объема единичного вырыва сводится к определению объема фигуры, ограниченной векторами l.
С целью построения математической модели [2] обозначим молекулы, на которые направлены векторы l (рис. 2, в), и присвоим вектору индекс той молекулы, на которую он направлен. Особо отметим, что векторы l1...l8 лежат на поверхности тела, векторы l9...l13 направлены от поверхности вглубь тела. Построим модель объемного тела, построенного на вершинах 18 векторов в трехмерном пространстве. Предположим, что данное тело представляет собой эллипсоид вращения. Объем фигуры, ограниченной векторами, можно определить по зависимости
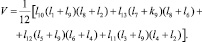
Из практики известно, что адгезионный вырыв осуществляется на глубину значительно больше, чем межмолекулярное расстояние двух соседних молекул. По этой причине нельзя сказать, что адгезионный износ происходит на глубину, не превышающую межмолекулярное расстояние в элементарной ячейке. Молекула, находящаяся внутри объема тела, взаимодействует с большим числом соседних молекул kk, чем молекула, расположенная на поверхности тела и имеющая определенное число некомпенсированных связей v1. Причем общее число возможных соседних молекул k = kk + v1 определяется из кристаллической решетки тела.
Числовое значение векторов l определяется факторами, определяющими адгезионный вырыв. При этом следует учесть, что реальные профили поверхностей имеют неровности, такие как шероховатость и субшероховатость. Таким образом, адгезионная связь Fвз образуется на поверхностях, расположенных по отношению друг к другу под определенным углом γ. От величины угла γ зависит величина вектора l, так как часть объема тела, расположенная ближе к вершине неровности, легче поддастся вырыву. Тогда выражение для l имеет вид
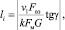
где G – модуль сдвига; k – возможное число соседних молекул; kk = k – v1 – реальное число соседних молекул.
Следует учесть, что векторы, направленные вглубь тела, имеют число соседних молекул, равное общему числу возможных молекул kk = k, тогда для векторов, расположенных на поверхности
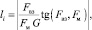
направленных вглубь тела
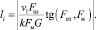
С целью проверки предложенной теории были проведены экспериментальные исследование образцов на установке САВ-10. Перед проведением эксперимента образцы из стали 45 (Ra = 0,025) очищали полярным и неполярным растворителем. С целью фиксации поверхности до испытаний (рис. 3, а) образцы исследовались на оптическом микроскопе MicroCapture20000.
Адгезионная связь считалась образованной, когда образец 2 не отсоединялся от образца 1 под действием силы тяжести. Образец 2 соединяли с датчиком силы, образец 1 жестко закрепляли на поверхности установки. Прикладывая усилия к датчику, смещали образец 2. Адгезионная связь считалась разорванной в момент, когда происходило смещение одного образца относительно другого, после чего поверхности образцов исследовались под микроскопом (рис. 3, б). Образовавшиеся темные пятна считали вырывами, образовавшимися в результате адгезионного износа.
Площадь поверхности и глубину вырывов определяли по 10 пятнам на 6 снимках поверхности, после чего полученные значения усреднялись. Объем вырыва рассчитывали как половину объема эллипсоида
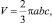
где a, b, c – полуоси эллипсоида.
По приведенным выше зависимостям рассчитывали объем единичного вырыва исходя из условий, что исследуемая сталь имеет аустенитную структуру k = 18, модуль сдвига стали G = 79?109 Па, расстояние между центрами частиц r = 3,495 нм [7], компенсированное расстояние z0 = 2,86 Å [3], константа Гамакера Aн = 45?10–24 Дж [7]. Силу межмолекулярного взаимодействия и силу адгезии можно определить по зависимостям, предложенным в работе [4].


а б
Рис. 3. Поверхность стали 45: а – до образования адгезионных вырывов; б – после образования адгезионных вырывов
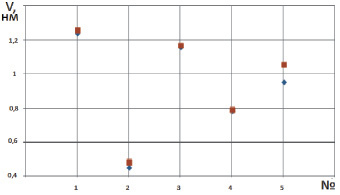
Рис. 4. Сопоставление экспериментальных данных  и результатов моделирования
и результатов моделирования  адгезионного вырыва стали 45
адгезионного вырыва стали 45
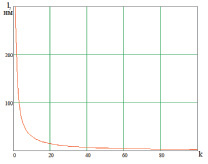
а б
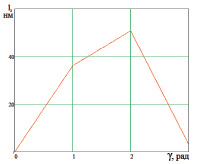
Рис. 5. Зависимость длины вектора износа: а – от угла наклона γ неровности к адгезионной связи (при k = kk); б – от числа возможных соседних молекул k (при γ = 68°)
Сопоставление экспериментальных данных и результатов моделирования приведено на рис. 4.
Таким образом, наблюдается близость экспериментальных и теоретических расчетов. По теоретическим выражениям были построены графики зависимости длины вектора износа l от угла наклона неровности γ (рис. 5, а) и от числа возможных соседних молекул k (рис. 5, б).
Как видно из представленных графиков, вектор l растет при значениях угла γ 0°…115° и снижается при значениях угла γ 116°...180°. С увеличением числа возможных соседних молекул износ уменьшается, что говорит о том, что чем больше молекул содержит элементарная ячейка и чем меньше расстояние между ними, тем она менее подвержена адгезии. Используя предложенную в работе [4] модель адгезионного износа, получили уравнение для определения объема единичного адгезионного вырыва. В соответствии с моделью адгезионного износа объем нелинейно зависит от угла наклона профиля и от кристаллической структуры стали. В дальнейшем, используя методы, предложенные в работах [1, 6], представляется возможным получить общее выражение для определения единичного адгезионного вырыва стали с любой структурой (заключение про пластическую и упругую деформации).



