Реакторный графит ГР-280 широко используется в качестве материала кладки активной зоны в уран-графитовых реакторах, в частности, в энергетических реакторах типа РБМК. Для обоснования работоспособности кладок этих реакторов были проведены исследования по влиянию реакторного облучения на размерную стабильность, механические и теплофизические свойства графита ГР-280 в интервале флюенсов 0,1–22?1025 м–2 (здесь и далее для Е > 0,18 МэВ) при температурах до 550 °С [4]. Было показано, что реакторное облучение приводит к сильной деградации теплопроводности графита, особенно быстрое падение теплопроводности наблюдается при облучении до малых флюенсов нейтронов (1?1025 м–2). При флюенсах около 5?1025 м–2 наблюдается стабилизация значений теплопроводности, однако при увеличении флюенсов до 15?1025 м–2 скорость падения теплопроводности демонстрирует тенденцию к увеличению.
В связи с повышением срока эксплуатации реакторов и, как следствие, с планируемым увеличением предельного флюенса нейтронов представляет интерес изучение теплопроводности при облучении графита до более высоких флюенсов 35?1025 м–2 с одновременным повышением температуры облучения до 650 °С, которая достижима в графитовых блоках наиболее энергонапряжённых каналов [5]. Кроме того, массив имеющихся результатов имеет тот недостаток, что из-за сложности высокотемпературных измерений коэффициента теплопроводности большинство результатов было получено при температурах измерения, не совпадающих с температурой облучения, что снижало достоверность результатов при рабочих температурах, полученных путем экстраполяции. В работе представлены экспериментальные зависимости коэффициента теплопроводности графита ГР-280 от флюенса нейтронов в интервале 5–32?1025 м–2 и температуры облучения в диапазоне 450–650 °С, а также выбрано аналитическое выражение для расчета коэффициента теплопроводности образцов в области высоких флюенсов нейтронов.
Материалы и методы исследования
Образцы графита марки ГР-280, представляющие собой таблетки размером ∅8×5 мм и ∅6×2 мм, были вырезаны методом электроискровой резки из прямоугольных блоков, полученных по стандартной электродной технологии, подробно описанной в работах [1, 10]. Вырезку осуществляли таким образом, чтобы оси таблеток располагались параллельно оси выдавливания блоков (образцы параллельной вырезки).
Образцы графита были облучены в реакторе БОР60 до флюенса нейтронов 5–32?1025 м–2 (Е > 0,18 МэВ) при температурах 450–650 °С.
Коэффициент теплопроводности образцов рассчитывали по формуле [5]:
λ = а?ρ?сp, (1)
где λ – коэффициент теплопроводности, Вт/(м·К); а – коэффициент температуропроводности, м2/с; ρ – плотность, кг/м3; сp – удельная теплоемкость, Дж/(кг?К).
Коэффициент температуропроводности измеряли на таблетках размером ∅8×5 мм методом лазерной вспышки на установке LFA 427 в соответствии со стандартом ASTM C 714-72 [11], погрешность измерения составляла 5 %.
Измерение удельной теплоемкости проводили на таблетках размером ∅6×2 мм методом дифференциальной сканирующей калориметрии на установке DSC 404 F1. Измерения проводили в среде аргона, скорость нагрева составляла 20 °С/мин.
Плотность образцов измеряли геометрическим методом с погрешностью 5 %.
Результаты исследования и их обсуждение
На графиках (за исключением рис. 1) и в тексте приведены коэффициенты теплопроводности, измеренные при температуре, равной температуре облучения, а флюенсы указаны для нейтронов с энергией выше 0,18 МэВ.
Зависимость коэффициента теплопроводности исходного графита (λисх) от температуры испытания (Тисп) приведена на рис. 1. При Тисп = 20 °С значение λисх составляет 125 Вт/м?К, с увеличением Тисп до 1200 °С оно уменьшается приблизительно в 2,7 раза. Высокое абсолютное значение λисх при Тисп = 20 °С, а также тот факт, что максимальное значение λисх находится ниже комнатной температуры (учитывая, что зависимость коэффициента теплопроводности графита от Тисп имеет форму купола), свидетельствует о чистоте графита и совершенстве его кристаллической структуры [2, 3].
На рис. 1 представлены также зависимости удельной теплоемкости исходного и облучённого графита (сpисх и сpобл) от температуры испытания. Как видно из графика, облучение не оказывает значительного влияния на величину удельной теплоемкости, так как в пределах погрешности эксперимента сpисх и сpобл совпадают. Поэтому далее при расчёте коэффициента теплопроводности облучённых образцов (λобл) по формуле (1) использовали сpисх. Слабое влияние реакторного облучения на сp графита ранее также отмечали в работе [3].
После облучения теплопроводность графита уменьшается. Как видно из рис. 2, величина относительного изменения коэффициента теплопроводности ?λ/λисх = (λобл – λисх)/λисх немонотонно спадает с возрастанием флюенса нейтронов для всех температур облучения (Тобл).
Для всех температур облучения можно выделить три интервала флюенса нейтронов (γ), в которых зависимость от него коэффициента теплопроводности различается: 1-й интервал – это интервал малых флюенсов (до 5?1025 м–2), где наблюдается резкое падение величины ?λ/λисх; 2-й интервал – это интервал промежуточных флюенсов (5?1025 –15?1025 м–2), где изменение ?λ/λисх незначительно; и 3-й интервал – это интервал флюенсов выше 15?1025 м–2, где вновь начинается ускорение темпов падения λ.
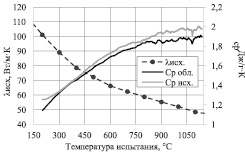
Рис. 1. Зависимость удельной теплоёмкости исходного и облучённого графита ГР-280 (Тобл = 450, флюенс 16·1025 м–2) и коэффициента теплопроводности исходного графита от температуры испытания
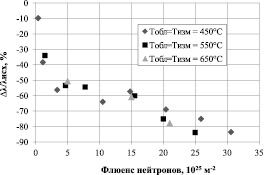
Рис. 2. Зависимость от флюенса нейтронов относительного изменения коэффициента теплопроводности графита ГР-280
Общепринято, что на первой стадии происходит падение λ за счет ускоренного накопления радиационных дефектов [2, 3], в данном случае вакансий и их малых комплексов. На второй стадии имеет место стабилизация концентрации дефектов из-за возрастающего количества стоков. Такое изменение λ является типичным для большинства материалов под облучением. Появление третьей стадии, связанной с ускоренным падением величины λ, является специфическим эффектом, характерным для графита.
Зависимость коэффициента теплопроводности от температуры облучения λобл(Тобл) представлена на рис. 3. Зависимость λобл(Тобл) для флюенса 0,5?1025 м–2 построена с привлечением экспериментальных данных из работы [9]. При облучении образцов до флюенса меньше 5?1025 м–2 величина λобл увеличивается с увеличением Тобл, а при облучении образцов до флюенса больше 5?1025 м–2 – наоборот, уменьшается. Так, при облучении до флюенса 15?1025 м–2 величина λобл уменьшается на 50 %, а при облучении до флюенса 0,5?1025 м–2 увеличивается на 10 % при увеличении Тобл от 450 до 650 °С.
Увеличение теплопроводности с увеличением Тобл, которое наблюдается при малых флюенсах, находится в соответствии с существующими представлениями, что увеличение Тобл приводит к дополнительному отжигу радиационных дефектов и, следовательно, к увеличению λобл. Уменьшение λобл при увеличении Тобл, наблюдаемое на образцах графита, облучённых до высокого флюенса, по нашему мнению, является специфическим эффектом, присущим графиту.
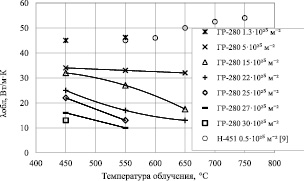
Рис. 3. Зависимость коэффициента теплопроводности облучённого графита ГР-280 от температуры облучения
Мы полагаем, что причиной упомянутых выше особенностей изменения теплопроводности в зависимости от флюенса и температуры облучения при больших флюенсах является накопление микротрещин, образующихся в графите из-за значительного радиационного анизотропного изменения размеров кристаллитов, которые приводят к большим внутренним напряжением и растрескиванию графита.
В пользу того, что поведение λ графита в области высоких флюенсов контролируется трещинообразованием, свидетельствуют данные рис. 4, где сопоставляются зависимости от флюенса нейтронов относительного изменения коэффициента теплопроводности (?λ/λисх) и относительного изменения объема образца (?V/Vисх), полученные в данной работе и приведённые в работе [5] соответственно. Образцы были взяты из одной партии и облучались в одних и тех же условиях. Ускоренный рост Vобл при облучении образцов до флюенсов выше 20?1025 м–2 вызван активным зарождением и ростом микротрещин [5]. В этом же диапазоне флюенсов (от 20?1025 м–2 и выше), как видно из рис. 4, происходит и ускоренное падение λобл.
Аналитическое описание зависимости теплопроводности от параметров облучения
Прямой расчет коэффициента теплопроводности облучённого графита от флюенса нейтронов и температуры облучения на данный момент невозможен ввиду недостатка знаний о радиационных дефектах и процессах рассеяния фононов на различных препятствиях. В настоящее время предпринимаются попытки создания полуэмпирической зависимости величины λобл от параметров облучения с использованием базы уже имеющихся экспериментальных результатов.
Наиболее известным является выражение, представляющее собой модификацию фундаментального уравнения Дебая для рассеяний тепла в материале по фонон-фононному механизму, предложенное в работе [7]:
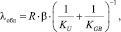(2)
где λобл – коэффициент теплопроводности облучённого графита; β – структурный множитель, учитывающий пористость, ориентацию образца и др. (для большинства марок реакторного графита он не зависит от температуры и равен 0,6); Ku, R и KGB – коэффициенты, учитывающие фонон-фононное рассеяние, рассеяние фононов на дефектах решетки и на границах зерен соответственно.
Зависимости R, KGB и Ku от температуры облучения и флюенса были определены экспериментально из широкого массива данных [8, 12, 13]. Используя эти зависимости и уравнение (2), авторы рассчитали коэффициенты теплопроводности образцов, облучённых до флюенса 5?1025 м–2 и выше при температурах 450–700 °С (рис. 5). Сравнение рассчитанных значений λобл с экспериментальными, полученными в данной работе, показывает их принципиальное отличие.
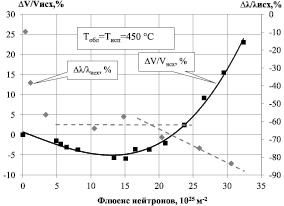
Рис. 4. Зависимость от флюенса нейтронов относительного изменения коэффициента теплопроводности и относительного изменения объёма образцов графита ГР-280, облучённого при 450 °С
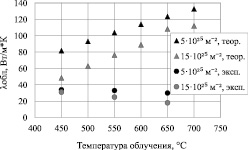
Рис. 5. Зависимость теоретических (рассчитанных по формуле (2)) и экспериментальных значений коэффициента теплопроводности облучённого графита ГР-280 от температуры облучения
Причиной этого мы считаем тот факт, что для формирования выражения R(γ, Tобл) использовался массив данных, полученный при малых флюенсах (до 1 сна), и поэтому оно не учитывает интенсивное образование в графите микротрещин при высоких флюенсах.
Для оценки коэффициента теплопроводности при высоких флюенсах, по нашему мнению, более перспективным представляется уравнение, предложенное в работе [6], которое связывает изменение коэффициента теплопроводности с распуханием образца при облучении:
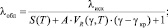(3)
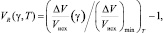(4)
где λисх, λобл – коэффициент теплопроводности исходного и облучённого графита; Vисх – исходный объём образца; S – относительное изменение термосопротивления (1/λобл) в интервале флюенсов, где зависимость коэффициента теплопроводности от флюенса выходит на плато (2 стадия); γ – флюенс быстрых нейтронов, 1025 м–2; γкр – критический флюенс (флюенс, при котором объем образца после стадии усадки возвращается к своему исходному значению), 1025 м–2; ?V/Vисх – относительное изменение объема образца при Тобл; (?V/Vисх)min – минимальное относительное изменение объема образца при Тобл; А – экспериментальный множитель, равный –0,1.
Для практического использования этой формулы необходимо определить зависимости от параметров облучения отдельных её членов. Данные относительного изменения объема образцов графита ГР-280 под облучением взяты из работы [5]. Все образцы для измерения объёма и коэффициента теплопроводности относятся к одной партии и облучены в одних и тех же условиях.
Зависимость коэффициента теплопроводности исходного графита от Тисп (рис. 1) можно аппроксимировать функцией
λисх = 16912/Т + 35,917. (5)
Значения величины S, усреднённые по нескольким маркам реакторного графита [6], а также для графита ГР-280, полученные в данной работе, представлены на ри. 6. В интервале температуры облучения 400–900 °С зависимость S(Тобл) описывается линейной функцией
S = –0,002·T + 2,67. (6)
Температурные зависимости γкр нескольких марок отечественного и зарубежного реакторного графита, включая наши данные, приведены на рис. 7, из которых видно, что в интервале Тобл от 300 до 850–900 °С величина γкр практически линейно спадает с увеличением Тобл и зависимость γкр от Тобл можно описать функцией следующего вида:
γкр = –0,033·Т + 37,5. (7)
Функция VR(γ, T) может быть преобразована следующим образом:
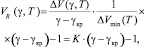(8)
где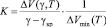 
представляет собой относительную скорость распухания графита.
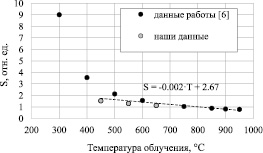
Рис. 6. Зависимость величины S реакторного графита от температуры облучения
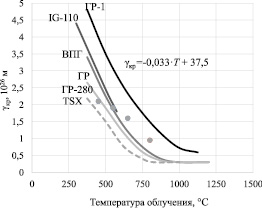
Рис. 7. Зависимость критического флюенса нейтронов реакторного графита от температуры облучения [2]
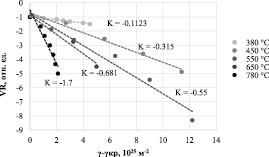
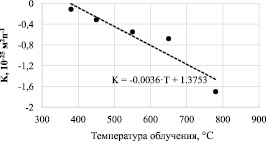
На рис. 8 а приведены графики зависимости VR(γ, T) от флюенса нейтронов, которые можно аппроксимировать прямыми линиями, что указывает на то, что величина K не зависит от флюенса нейтронов. Зависимость величины K, равной тангенсу угла наклона кривых на рис. 8, а, от Тобл, представлена на рис. 8, б и может быть аппроксимирована функцией
K = –0,0036·Т + 1,3753. (9)
Формула (3) с соответствующими уравнениями (4)–(9) представляет собой аналитическую зависимость коэффициента теплопроводности графита ГР-280 от температуры облучения и флюенса нейтронов в области флюенса нейтронов выше критического. График этой зависимости вместе с имеющимися экспериментальными точками приведен на рис. 9. Видно, что с увеличением Тобл в интервале 450–800 °С, типичном для эксплуатации в реакторах РБМК, величина λобл резко падает до значений ниже 5 Вт/м·К.
Отметим, что формула адекватно описывает экспериментальные результаты до Тобл 750–800 °С. Это связано, по нашему мнению, с тем, что зависимость γкр от Тобл (рис. 7), которую мы считали линейной, при Тобл выше 800 °С имеет явную тенденцию к затуханию, и, следовательно, формула (7) должна быть скорректирована с учетом этого эффекта.
Принимая во внимание, что многие марки российских и зарубежных графитов по своей структуре и конечной термообработке аналогичны графиту ГР-280, можно полагать, что полученная аналитическая зависимость может быть полезна при оценке коэффициента их теплопроводности.
а
б
Рис. 8. Экспериментальные точки и график функции VR(γ, T): а – общий вид; б – зависимость углового коэффициента функции VR(γ, T) от температуры облучения
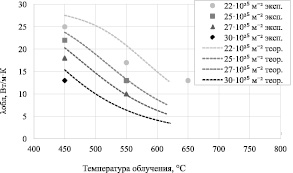
Рис. 9. Экспериментальные и рассчитанные по формуле (3) значения коэффициента теплопроводности облучённого графита ГР-280 в зависимости от температуры облучения. Температура измерения равна температуре облучения
Заключение
1. В работе представлены экспериментальные зависимости коэффициента теплопроводности графита ГР-280 от флюенса нейтронов в интервале 5–32·1025 м–2 и температуры облучения в диапазоне 450–650 °С. Измерения λобл выполнены при Тисп = Тобл.
2. На кривой зависимости λобл от флюенса нейтронов отмечено три стадии: первая стадия (0–5?1025 м–2), характеризующаяся резким падением ?λ/λисх, составляющим примерно 55 %; вторая стадия (5?1025–15?1025 м–2), где изменение величины ?λ/λисх незначительно и равняется приблизительно 5 %, и третья стадия (выше 15?1025 м–2), где начинается ускоренное по сравнению со второй стадией падение величины ?λ/λисх.
3. Зависимость теплопроводности от температуры облучения определяется флюенсом нейтронов: при облучении до флюенсов ниже 5?1025 м–2 λобл увеличивается с увеличением Тобл, а при флюенсах выше 5–10?1025 м–2 – уменьшается. Уменьшение коэффициента теплопроводности в интервале температур облучения 450–650 °С при флюенсе 22?1025 м–2 достигает 50 %.
4. Приведены аргументы того, что специфические эффекты, обнаруженные в характере зависимости теплопроводности от флюенса и температуры облучения при флюенсах больше критического, являются следствием накопления в графите под облучением микротрещин, которые образуются из-за значительного анизотропного изменения размеров кристаллитов.
5. Для аналитического описания полученных результатов было применено выражение, связывающее изменение коэффициента теплопроводности с распуханием образцов при облучении до флюенса нейтронов выше критического. С использованием доступных экспериментальных данных рассчитаны необходимые коэффициенты и построены расчетные зависимости λобл от флюенса и температуры облучения. Отмечено хорошее совпадение экспериментальных и расчетных значений коэффициента теплопроводности в интервале температур облучения 400–850 °С.